這篇博文的目的是解釋數據可用性採樣(DAS)的基本原理,它所依賴的模型,以及在實踐中實施該技術時的挑戰和未解決問題。
原文:Data Availability Sampling: From Basics to Open Problems (paradigm)
作者:joachimneu
譯者:Evelyn,W3.Hitchhiker
封面:Photo by and machines on Unsplash
介紹
任何 layer 1 區塊鏈的核心責任都是保證數據可用性。這一保證對於客戶能夠解釋 layer 1 區塊鏈本身是至關重要的,同時也是更高層應用(如 rollups)的基礎。為此,一種經常被討論的技術是用於數據可用性驗證的隨機採樣,出現於由 Mustafa Al-Bassam、Alberto Sonnino 和 Vitalik Buterin 在 2018 年的一篇論文中,並被推廣。該技術是 Celestia 區塊鏈的核心,並被提議與 “Danksharding” 一起納入以太坊權益證明(PoS)中。
這篇博文的目的是解釋數據可用性採樣(DAS)的基本原理,它所依賴的模型,以及在實踐中實施該技術時的挑戰和未解決問題。我們希望這篇文章能給研究人員"吃下一劑藥丸",吸引他們關注這個問題,並激發新的想法來解決一些懸而未決的挑戰(參考最近以太坊基金會的提案請求)。
問題
有人(如 L1 區塊提議者或 L2 排序者)產生了一個數據塊。他們聲稱已經向"公眾"證明了該數據是可用的。你的目標是檢查可用性的說法,也就是說,如果你需要,你是否真的能夠獲得這些數據?
數據的可用性是至關重要的。基於 Optimistic 的欺詐證明系統,如 Optimism,需要數據可用性來進行驗證,甚至基於有效性證明的系統,如 StarkNet 或 Aztec,也需要數據的可用性來確保其的活躍性(例如,證明資產所有權以用於 rollup 的逃生艙口或強制交易包含機制)。
對於到目前為止的問題表述,有一個簡單的"幼稚"測試程序,像比特幣這樣的早期系統也隱含地採用:只需要下載整個數據塊便能進行驗證。如果你成功了,你就知道它是可用的;如果你沒有成功,你就認為它不可用。然而現在,我們想在不用自己下載過多數據的情況下測試數據的可用性,例如,因為數據大到我們無法處理,或者因為"僅僅"為了驗證數據的可用性而在我們並不真正感興趣的數據上花費大量帶寬似乎十分浪費。在這一點上,我們需要一個模型來闡明只下載或保留"部分數據"的"含義"。
模型
計算機科學中一個常見的方法是,首先在一個具有相當豐富的設施的模型中描述一項新技術;然後解釋該模型如何實現。我們對 DAS 採取了類似的方法,但正如我們將看到的,當我們試圖將模型實例化時,就會突然出現有趣的開放式研發問題。
在我們的模型中,在一個黑暗的房間裡有一個公告板(見下面的漫畫)。首先,區塊生產者進入房間,並獲得在公告板上寫下一些信息的機會。當區塊生產者退出時,它可以給你(驗證者)一小段的信息(其大小與原始數據不呈線性比例)。你帶著手電筒進入房間,手電筒的光束很窄,而且電池電量不足,所以你只能讀取到公告板上很少的幾個明顯位置的文字。而你的目標是讓自己相信,區塊鏈生產者確實在公告板上留下了充足的信息,所以如果你打開燈,閱讀完整的公告板,你將能夠恢復文件。
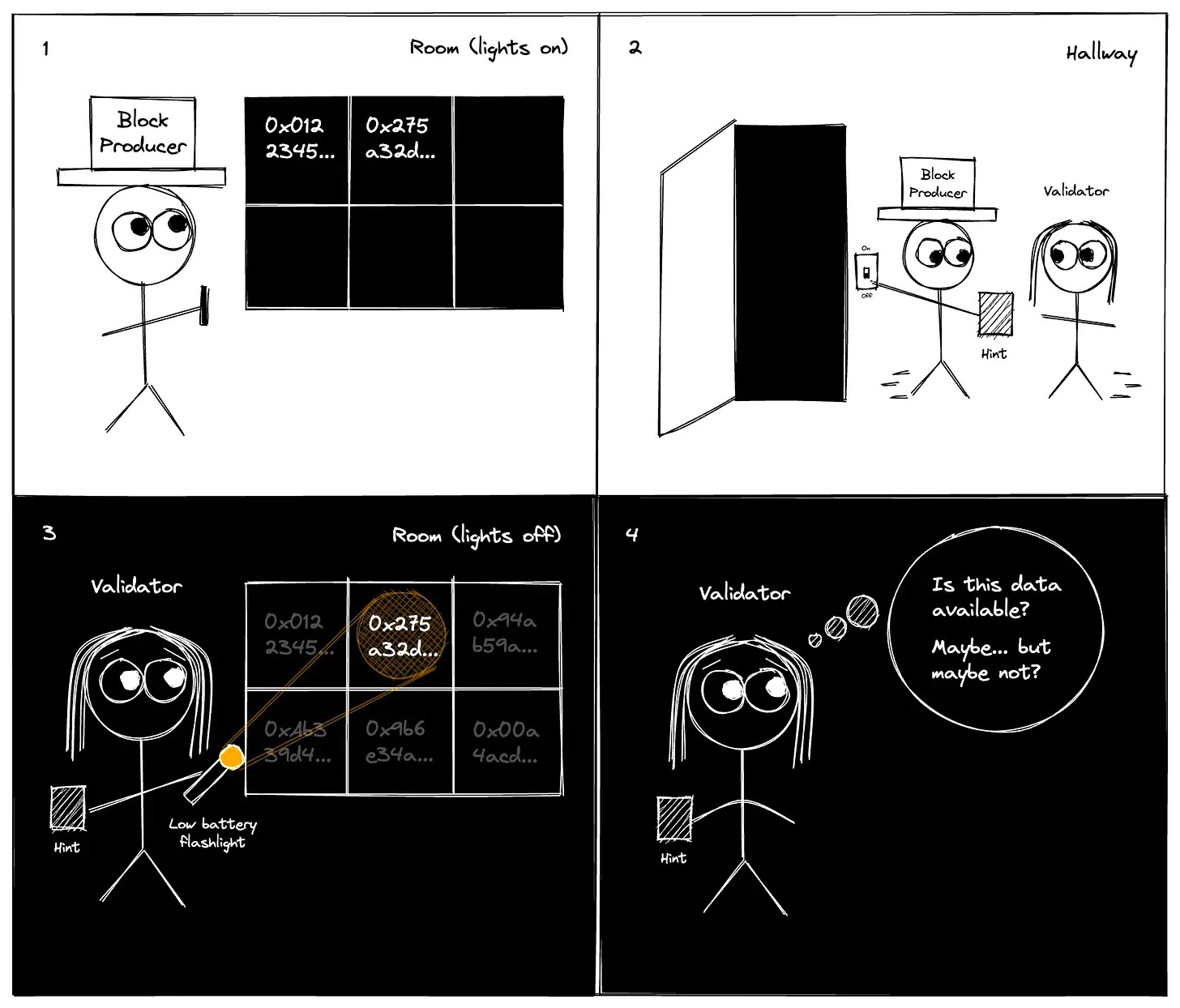
起初,這似乎很棘手:我們可以要求區塊生產者在公告板上寫下完整的文件。現在考慮兩種可能性:要么生產者行為誠實,寫下完整的文件,要么生產者行為不端,遺漏了一些小塊的信息,使整個文件無法使用。通過只在幾個地方檢查公告板,你無法可靠地區分這兩種情況—— 因此,你無法準確地檢查數據可用性。我們需要一種新的方法!
(理論)解決方案
這就是 Reed-Solomon 碼發揮作用的地方。讓我們簡單地回顧一下這些內容。在高層次上,糾刪碼的工作原理是這樣的:一個由 k 個信息塊組成的向量被編碼成一個由 n 個編碼塊組成的(更長的!)向量。編碼的比率 R = k/n 衡量了編碼所引入的冗餘。隨後,我們可以從編碼塊的某些子集中解碼出原始信息塊。
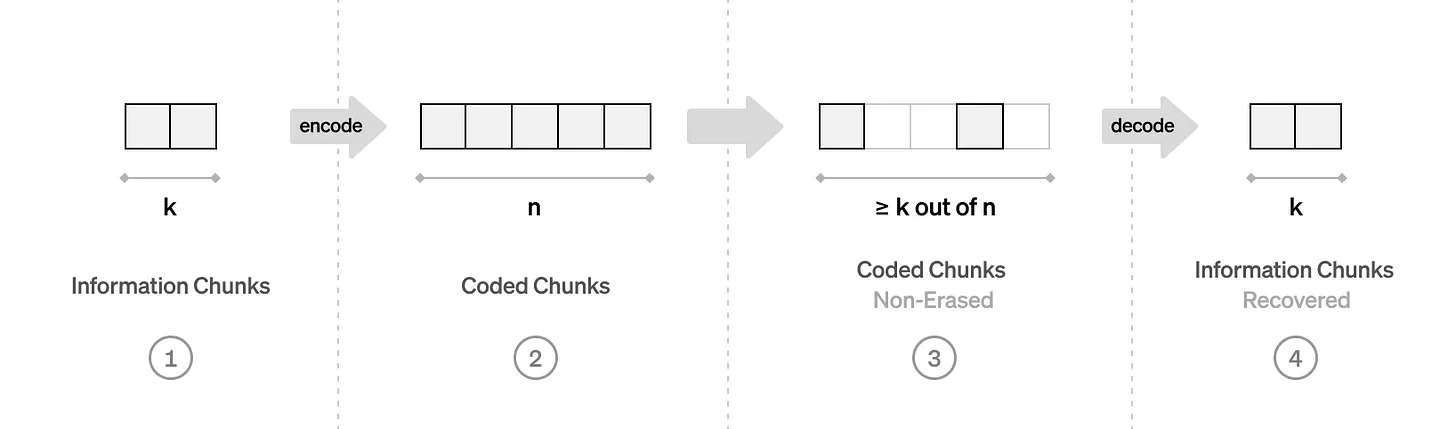
如果編碼是最大距離可分的(MDS),那麼原始的 k 個信息塊可以從任何大小為 k 的編碼塊子集中恢復出來,這是一個有用的效率和魯棒性保證。Reed-Solomon 碼是一個流行的 MDS 編碼系列,其工作原理如下。記得在學校裡,你可能學過兩點唯一決定一條線。

這是因為一條直線可以被描述為一個有兩個係數的 1 次多項式:y = a1x+a0(現在我們假設各點有不同的 x 坐標)。事實上,這一見解可以被概括為:任何次數為 t-1 的多項式,對應於描述多項式的一組係數
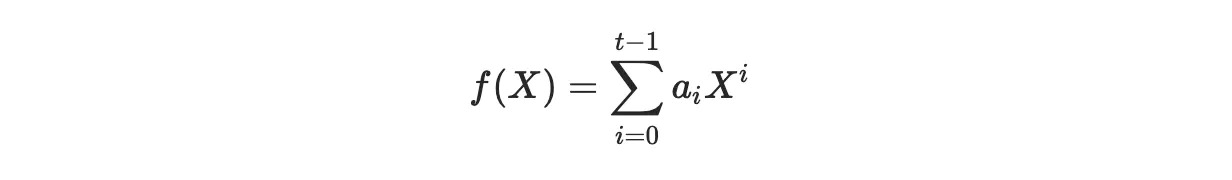
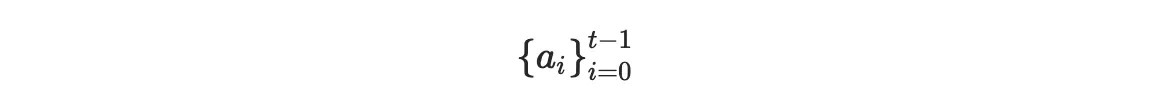
由該多項式經過的任何 t 個點(有不同的 x 坐標)唯一決定。換句話說:一旦你知道多項式在 t 個不同位置的求值,你就可以得到它在任何其他位置的求值(首先恢復多項式,然後求值)。
Reed-Solomon 碼就是根據這一觀點建立的。對於編碼,我們從 k 個信息塊
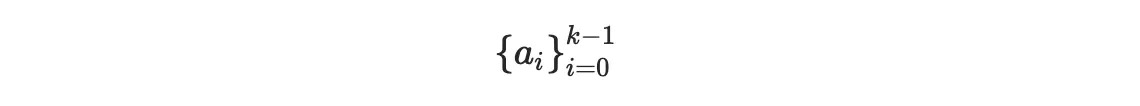
開始,構建相關的多項式
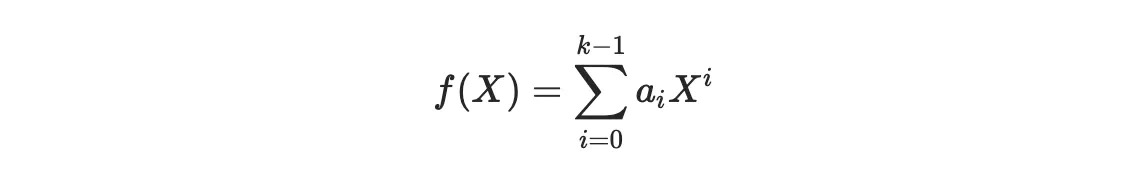
並在 n 個不同的 x 坐標上對其進行求值,從而得到編碼的信息塊。現在,由於上述見解,這些編碼塊中的任何 k 都允許我們唯一地恢復 k-1 次的多項式,並讀出係數以獲得原始信息塊。Voilà!
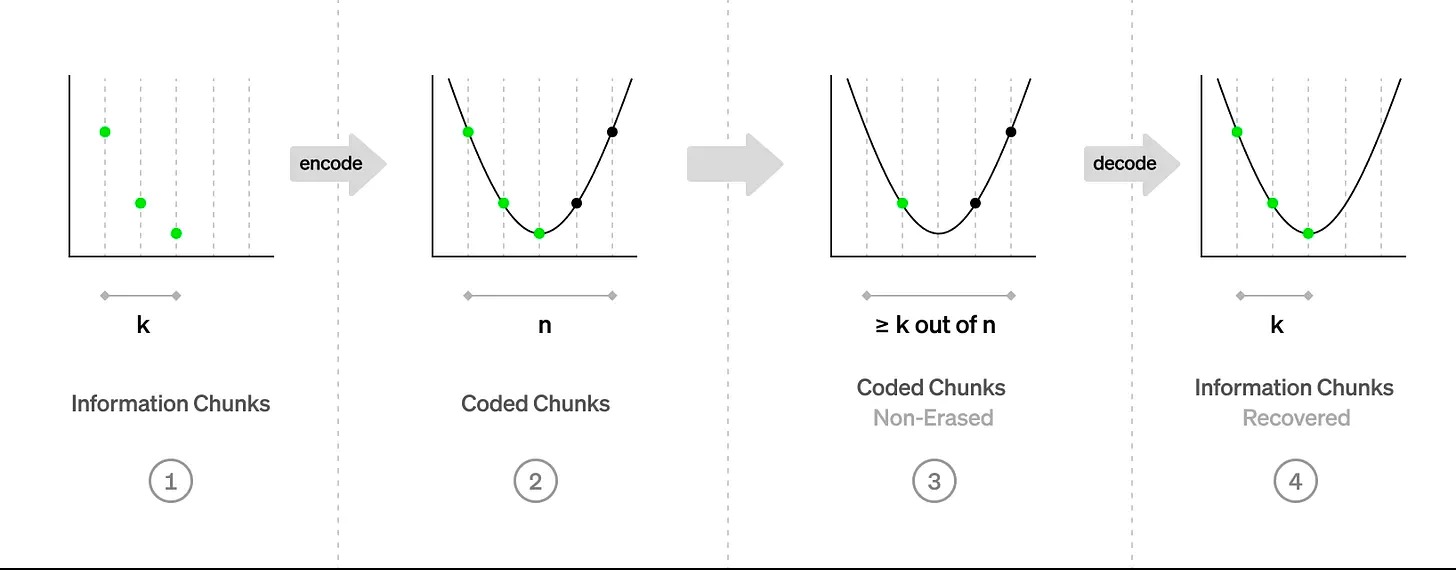
回到我們的數據可用性問題:我們現在不再要求區塊生產者在公告板上寫下原始文件,而是要求它將文件切分成 k 個小塊,用比率為 R=1/2 的 Reed-Solomon 碼對它們進行編碼,並將 n=2k 編碼塊寫到公告板上。現在我們假設區塊生產者至少誠實地遵循編碼(我們將在後面看到如何解除這一假設)。再考慮一下這兩種情況:要么生產者行為很誠實,寫下了所有的塊,要么生產者行為不端,想保持文件不可用。回顧一下,我們可以從 n=2k 個編碼塊中的任何 k 個來恢復原始文件。因此,為了保持文件不可用,區塊生產者最多可以寫入 k-1 個塊。換句話說,現在至少有 k+1 個,也就是 n=2k 個編碼塊中的一半以上,將被丟失!
但是現在這兩種情況,一個完全寫滿的公告板,和一個半空的公告板,是很容易區分的。你在少量 r 個隨機採樣的位置檢查公告板,如果每個採樣的位置都有各自的塊,則認為文件是可用的,如果任何一個採樣的位置是空的,就認為是不可用的。請注意,如果該文件不可用,因此(超過)一半的公告板是空的,你錯誤地認為該文件可用的概率小於
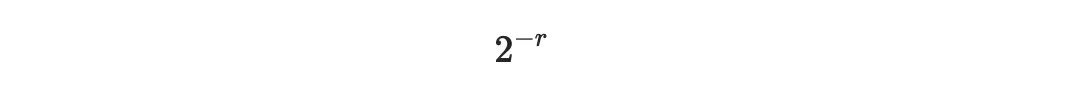
即在 r 中呈指數級減小。
(實際)挑戰
這是非常簡單的(在給定的"黑房間中的公告板"模式中)。讓我們思考一下這個模型。這些組件代表什麼?我們能在一個真正的計算機系統中實現它們嗎,如何實現?
事實上,為了幫助各位發現理論與實踐之間的差距,我們用那種"奇怪的""黑房間裡的公告板"的模型來解釋問題和解決方案,其隱喻與真實的計算系統幾乎沒有任何相似之處。這是為了鼓勵你思考真實世界和模型世界的各個方面是如何相對應的,以及它們可能(無法)是如何實現的。如果你剩下的模型碎片還不能轉化為計算機/網絡/協議的等價物,你就知道還有一些事情要做(這可能是你理解上的差距,或者是開放的研究問題!;)
這裡收集了一些非詳盡的挑戰,對於其中一些挑戰,多年來社區已經找到了合理的答案,而其他的挑戰仍然是開放的研究問題。
**挑戰 A:如何確保公告板上的塊確實是由提議者寫的?**思考一下被採樣的塊在網絡上以任何形式傳送到採樣節點時會發生的改變。這就是一小塊信息的來歷,當生產者離開並且採樣節點進入黑房子時,區塊生產者可以將其傳遞給採樣節點。在實踐中,這被實現為對寫在公告板上的原始內容的綁定向量承諾(想想 Merkle 樹),並且它被作為塊頭的一部分進行共享。給定這個承諾後,區塊生產者可以在公告板上留下每個編碼塊的證明,以表明該塊確實是由區塊生產者寫的。區塊在運輸過程中不能被第三方改變,因為承諾方案是不允許為一個被修改過的區塊偽造有效的證明。請注意,這本身並不排除區塊生產者在公告板上寫入無效/不一致的塊,這一點我們在接下來會討論。
**挑戰 B:確保區塊生產者正確地進行糾刪碼編碼。**在上述方案中,我們假設區塊生產者對信息塊進行了正確的編碼,所以糾刪碼的保證是成立的,因此,我們實際上是可以從足夠多的編碼塊中恢復信息塊的。換句話說,區塊生產者所能做的就是保留信息塊,而不是用無效的信息塊來混淆我們。在實踐中,有三種常見的方法來排除無效的編碼:
- **欺詐證明。**這種方法依賴於這樣一個事實,即一些採樣節點足夠強大,可以採樣很多的塊,以至於它們可以發現塊的編碼不一致,並發出無效的編碼欺詐證明,將有關文件標記為不可用。這方面的工作旨在最大限度地減少節點必須檢查的塊的數量(並作為欺詐證明的一部分轉發),以檢測欺詐(參見 Al-Bassam/Sonnino/Buterin 的原論文為此使用二維 Reed-Solomon 碼)。
- **多項式承諾。**這種方法使用 KZG 多項式承諾作為塊頭中包含的綁定向量承諾來解決挑戰 A。多項式承諾允許根據對未編碼信息塊的承諾直接驗證 Reed-Solomon 編碼塊,因此沒有為無效編碼留下空間。可以認為:向量承諾和 Reed-Solomon 碼在多項式承諾中是不可分割的。
- **有效性證明。**一個可以用來證明向量承諾提交的編碼塊是正確糾刪碼的加密證明系統。這種方法是一個很好的教學"心理模型",並且在所採用的糾刪碼方面是通用的,但在相當長的一段時間內可能是低效率的。
**挑戰 C:公告板是"什麼"和"在哪裡"?提議者如何"寫"到它上面?**在我們討論公告板"是什麼"和"在哪裡",提議者如何"寫"到它上面,以及驗證者如何從它"讀"/"取樣"之前,讓我們回顧一下兩個基本 P2P 網絡原語中眾所周知的缺點:
- 基於低量級泛洪的發布-訂閱 gossip 網絡,如 GossipSub,其中通信被組織成不同的"廣播組"("主題"),參與者可以加入("訂閱")並發送消息("發布")到:
- 在任意("拜占庭")對抗行為(例如,日蝕攻擊、Sybil 攻擊、對等發現攻擊)下不安全
- 常見的變體甚至不提供抗 Sybil 抵抗機制
- 通常不保證參與者的小組成員對其他參與者的隱私(事實上,小組成員身份通常與對等方通信,以避免他們轉發不需要的主題網絡流量)。
- 如果有大量的主題,每個主題都有很少的訂閱者,那麼通信往往會變得不可靠(因為訂閱了特定主題的節點的子圖可能不再連接,所以泛洪可能會失敗。)
- 分佈式哈希表(DHT),如 Kademlia,每個參與者都存儲了哈希表中存儲的全部數據的一部分,參與者可以快速確定通往存儲特定信息的對等方的最短路徑。
- 也不是拜占庭式的容錯(例如,對誠實參與者的請求進行不適當的路由,對網絡形成/維護攻擊)
- 事實上,DHT 在抵禦對抗行為方面的表現比 gossip 協議差很多。Gossip 協議"只"要求由誠實節點(以及誠實節點之間的邊)形成的子圖是連接的,因此信息可以從任何誠實節點到達所有誠實節點。在 DHT 中,信息是專門沿著路徑路由的,查詢一旦到達路徑上的對抗節點就可能失敗。
- 也不提供 Sybil 抵抗機制
- 參與者存儲或請求信息的隱私不被保障(不被其他參與者的好奇心所影響)。
考慮到這一點,我們可以回到關於如何實現公告牌和對其進行讀寫操作的核心問題。編碼塊存儲在哪裡?它們如何到達那裡?正在考慮的三種主要的方法是:
- **GOSSIP:使用一個 gossip 網絡來分散編碼塊。**例如,每個編碼塊可以有一個主題,而負責存儲某個塊的節點可以訂閱相應的主題。
- **DHT:將編碼塊上傳到 DHT。**然後,DHT 將"自動"分配給每個參與者他們應該存儲的塊。
- **REPLICATE:來自附近的副本的採樣。**一些節點存儲完整(或部分)的數據副本,並向採樣節點提供塊請求。
這些方法所面臨的挑戰是:
- 如何確保"公告板上有足夠的空間"開始(即有足夠的參與者訂閱了 GOSSIP 的每個主題,或者每個節點可以存儲它在 DHT 下需要存儲的所有塊),並確保公告板的所有部分都在隨著節點的變化和時間的推移而保持在線?(理想情況下,為了確保可擴展性,我們甚至希望存儲能被有效地利用,也就是說,在誠實的節點存儲的內容中不應該有太多的冗餘)。在一個真正的無需許可系統中,這將是特別棘手的,在這個系統中,節點來來去去,也許沒有 Sybil 抵抗機制,所以大部分的節點可能是對抗性的,也可能在瞬間消失。幸運的是,在區塊鏈背景下,通常會有一些 Sybil 抵抗機制(如 PoS),可以用來建立信譽甚至進行攻擊,但如何利用 Sybil 抵抗機制來保證 P2P 網絡層的安全,其中還有許多細節有待確定。
- 根據前面的觀點,由於網絡是共識的基礎,因此也是拜占庭容錯(BFT)系統的基石,網絡層本身最好是 BFT —— 但正如前面所見,流行的 gossip 或 DHT 協議(如 GossipSub 或 Kademlia)並非如此。(即使是 REPLICATE 也可能面臨這種挑戰,因為 DHT 可能仍然用於網絡堆棧的其他部分,例如,用於對等節點的發現;但在這一點上,DHT 的挑戰成為一般網絡層的關注點,而不是專門針對數據可用性採樣。)
- 最後,有人認為,從長遠來看,節點應該存儲或轉發不超過一個區塊的相當小的一部分,否則可擴展性和支持相對"弱"的參與者(參照去中心化)的可能性是有限的。這是與 REPLICATE 是相反的。對於 GOSSIP 來說,這就需要大量的廣播組("主題"),每個主題都有少量的訂閱者,在這種情況下,gossip 協議往往變得不那麼可靠。在任何情況下,上述方法都有成本,例如,代表其他節點轉發塊的帶寬,不能超過單個節點的預算。
**挑戰 D:我們"如何"實現隨機採樣?**這個問題有兩個方面:所需的塊如何在網絡中定位和傳輸(即如何從公告板上"讀取"),以及如何確保採樣對對手來說"保持隨機",即對抗性區塊生產者沒有(太多的)機會根據誰查詢哪些塊而適應性地改變其策略。
- 當然,直接從區塊生產者那裡採樣並不是一個可行的選擇,因為這需要區塊生產者的高帶寬,而且如果區塊生產者的網絡地址被所有人知道的話,還會產生相關的拒絕服務向量。(可以通過 DHT 和 REPLICATE 的視角觀察到一些涉及到從區塊生產者那裡提取的混合結構)。
- 另一種方法是在使用上述方法之一(GOSSIP 或 DHT)分散大塊後,從"swarm "中採樣。具體來說:
- 在使用 GOSSIP 或 DHT 分散塊之後,DHT 在路由採樣請求和隨機採樣塊時會很方便,但這也帶來了上面討論的挑戰,最明顯的是缺乏 BFT 和隱私。
- 另外,在 GOSSIP 下,每個節點可以訂閱與它想採樣的塊相對應的主題—— 但有上述的挑戰:除了缺乏 BFT 和隱私,有大量的主題而每個主題的訂閱者很少會導致不可靠的通信。
- 在"從區塊生產者中採樣"和"從 swarm 中採樣"之間,可以用 REPLICATE 進行折衷,即從數據的完整副本中採樣,而副本是在網絡對等方中進行識別。
請注意,上面只解決了採樣(現在從公告板上"讀"),而沒有解決在未來任何時候從公告板上"讀"的問題。具體來說,GOSSIP 本質上實現了一個臨時的公告板(只能在其內容被寫入/散佈時被讀取/採樣),而 DHT 實現了一個永久的公告板(也可以在很久之後被讀取/採樣)。通常情況下,人們希望有一個永久的公告板(永久的要求從"天"到"永遠"不等,取決於具體的設計),為此,GOSSIP 必須使用 DHT 來路由塊,這就帶來了上述的挑戰。REPLICATE 馬上就實現了一個永久性的公告板。
下表說明了通常建議使用哪些 P2P 協議來實現模型的不同功能。具體來說,面向 gossip 的方法有兩種變體,一種是使用 gossip 對塊進行採樣,另一種是使用 DHT 對塊進行採樣,而在這兩種情況下,先使用 gossip 將塊寫在公告板上,然後再使用 DHT 從公告板上"讀取"。相比之下,面向 DHT 的方法完全依靠 DHT 來完成所有相關的操作。在面向 replication 的方法中,每個節點使用請求/響應協議,從附近的完整副本中讀取/採樣塊。儘管兩個對等方之間的 gossipping 在技術上可能是通過請求/響應協議實現的,但它有效地使用了 gossip 來進行塊的初始傳播。

此外,在上述所有技術中,"誰採樣了什麼"被(至少是部分)洩露給了攻擊者,因此攻擊者可以通過自己的行為,自適應地削弱/促進某些節點採樣的塊的傳播,從而欺騙某些節點相信該塊是(不可)可用的。雖然早期的工作表明,只有少數節點可以被欺騙,但這是不可取的。另外,早期的工作假設了匿名網絡通信,如果不是完全不切實際的話,這在實踐中至少會帶來相當大的性能損失。
**挑戰 E:如何"修復"公告板的內容?**也就是說,如果一個編碼塊丟失了(例如因為存儲該塊的節點離線了,這是如何發現的?),如何修復它?簡單的修復涉及到解碼和重新編碼,因此帶來了相當大的通信和計算負擔,特別是對於常見的 Reed-Solomon 糾刪碼。誰來承擔這一重任?他們是如何得到補償的?如何避免一個惡意的區塊生產者通過保留幾個編碼塊來破壞採樣節點,並迫使節點在昂貴的修復上花費資源?分佈式修復方案呢?甚至如何檢索修復所需的塊?這又回到了之前關於未來從公告板"讀取"的觀點。
**挑戰 F:激勵。**如果採樣是免費的,那麼如何防止拒絕服務向量?如果採樣需要付費(如何實施?),如何同時做到完全匿名?如何補償那些存儲公告板(部分)、在 P2P 網絡中傳遞信息或執行維護任務(如塊狀修復)的人?
另一種模型
為了完整起見,我們簡要地提到一個稍微不同的模型,DAS 實現了一個稍微不同的保證。即使沒有匿名和可靠的網絡,攻擊者最多可以欺騙一定數量的誠實節點,使其相信一個不可用的文件是可用的。否則,它將不得不釋放如此多的塊,以便從誠實節點獲得的所有塊的聯合中可以恢復該文件。這種模式的優點是,從網絡中要求的屬性更容易實現(特別是在 P2P 網絡被攻擊者破壞的情況下)。缺點是對個人用戶沒有具體的保證(你可能是少數被騙的人之一!),而且仍然不清楚如何收集所有由誠實節點獲得的樣本並恢復文件(特別是當 P2P 網絡被對手攻擊時)。
未來研究&發展方向
基於這篇博文中提出的觀察和論點,我們認為以下將是未來研究和發展的一些有趣方向:
很明顯,為了保證網絡層的安全,一些 Sybil 抵抗機制是必要的(現在,可以說,網絡協議經常隱含地依賴 IP 地址的稀缺性來達到這個目的,例如,GossipSub v1.1 的對等評分)。方便的是,共識層正好提供了這一點,例如,以權益證明的形式。因此,在網絡層上重用共識層的 Sybil 抵抗機制似乎是很自然的,例如,在 gossip 協議中從驗證者集合中採樣出一個節點(從而"繼承"共識的誠實多數假設的力量)。雖然這可能不會立即保證那些不積極的共識參與者的節點的網絡安全,但它可以幫助在共識節點之間建立一個安全的"骨幹"(從而加強共識的安全性),隨後也許會成為一個墊腳石,使每個人都有更好的安全。這條道路上的一個合乎邏輯的下一步是仔細分析共識和網絡與這種共享的 Sybil 抵抗機制的相互作用(這是在這個方向上最近邁出的第一步)。
- 改進的 gossip 和 DHT 協議:(參考本調查報告)
- 拜占庭容錯(BFT),特別是使用共識層上常見的 Sybil 抵抗機制
- 效率(特別是對於 BFT 變體,到目前為止,這些變體有相當大的成本和/或較低的對抗復原能力)。
- 隱私保證(改進的保證,以及更好的效率/更低的成本)。
- 修復機制:
- 以分佈式方式實施修復(具有局部性的糾刪碼?)
- 研究和設計相關的激勵機制
免責聲明:作為區塊鏈信息平台,本站所發布文章僅代表作者及嘉賓個人觀點,與 Web3Caff 立場無關。文章內的信息僅供參考,均不構成任何投資建議及要約,並請您遵守所在國家或地區的相關法律法規。