第一人稱視角解讀 Curve 設計理念
作者:observerdq
編排:黑羽小鬥
文章:Buidler DAO
封面:Curve
作者說
一年前,我做了一段時間 Uni V3 的 LP,玩得挺起勁。 大約也是那段時間,有一種說法,做 Curve Tricrypto Pool 的 LP 是相當穩健的持續生利的主流資產配置方式,這吸引我閱讀了一番 Curve V2 白皮書。 對 Uni 和 Curve 兩者的氣質有了一些朦胧的感覺,是有顯著差別的。 Uni 追求的是盡可能充分的自由市場,而 Curve 有一些精確的計劃經濟的氣味。
為了推進這個思考,自然有必要把 Curve V2 的技術細節理解透徹,於是幾個月前開始仔細研究 Curve V2。 作為曾經物理學科研人員的 Curve 創始人,Michael 在白皮書里自如地組合著一個個數學公式。 作為數理素人讀者,我費力地定位到了其中很核心、卻並不直觀好懂的元素,Xcp 以及相關的 D、Virtual Price。
研究過程中也意識到,即便高手,亦非一日練成大法,Curve V2 是在 V1 基礎上改造后的複雜化、通用化版本。 先去理解 Curve V1,能更清晰地把握設計的要義。 重走高手當年路。
V1 的主角是 A 和 D。 A 參數看似簡單,A 越大,在價格 1 附近分配的流動性越多,一句話就講完。 但當翻閱到當年的記錄時(Discord / 治理論壇 / Telegram),不斷地蹦出圍繞 A 的各種問題,有單純技術層面的,有和協定治理有關的,林林總總,極為豐富,這也是單寫 A 參數的緣起,下文是其中的一部分。 首先探討了 A 作為單個 DEX 的獨有參數,對整個市場的影響力。 一個有影響力的參數,它的管理便成了個重要問題,下文進一步探討了調控 A 的技術細節。
落筆於 A 參數這很微觀細碎的話題,倒也沒忘了初衷,沒忘了對 Uni vs Curve 氣質比較的最初興趣。 每每仍在嘗試提問,這些細節背後是否透露了一種根本性的理念差別呢?
—— dq
文章速覽
一. / A 參數和全市場價格決定的關係
/ A 參數可以影響市場價格嗎? AC 和反對方的各自陳述
/ A 參數對供給側的重要影響
/ 結語
二. / 調整 A 帶來的曲線變化及損益
/ 不同 A 值對應曲線的一個圖示
/ 訂單簿視角來看 A 值調整後的變化
/ A 調整帶來的損益 – 最直接的計算方式
/ 剔除無常的損益評估
/ 結語
全文 4741 字,預計閱讀時間 15 分鐘
一. A 參數和全市場價格決定的關係
2020 年 9 月 4 號,Andre Cronje 在 Curve 治理論壇裡發了一個 Proposal,希望把 y Pool 的 A 參數從 2000 調整到 1000。 引發了少量的討論,也有一些反對意見,幾天后還是很平靜地通過投票了。 看著像是沒什麼重大意義的主題,比起後來很多 DeFi 專案在一些事項上的廣泛大辯論,似乎不值一提。
正是 Curve 的數學複雜度抬高了討論門檻,掩蓋了一些問題的重要性,甚至阻礙了對 Curve 本質的理解。 本系列文章聚焦於 A 參數,回到上古時期,考察幾個歷史事件,嘗試把數學簡化,讓關於 Curve 的真正重要的一些命題顯現出來。 本文是第一篇,以 AC 的這個提案切入。
A 參數可以影響市場價格嗎?
AC 和反對方的各自陳述
回到 AC 的這個 proposal,8 月底 9 月初 yETH vault 極速擴張(yETH vault 的操作是吸儲 ETH,Mint DAI,存入 yDAI vault,也就是存入 Curve y Pool 做 LP,獲得 CRV 獎勵、賣成 ETH,進而實現 ETH 本位的收益)。
結果正好迎來了 ETH 快速下跌的行情,每當 ETH 急跌,DAI 的需求就大增。 y Pool 裡面 DAI 的份額跟著極速下降,最低到了只剩 2% 的樣子。
AC 認為 y Pool 的 A 參數過高了(A = 2000),使得 y pool 向市場供應了很多本不該那麼便宜的 DAI。 比如他的以下論述。

反對聲音主要圍繞兩個角度,其中一個角度和 yETH vault 持續賣出 CRV 帶來的拋壓有關,這裡暫不展開。
令我感興趣的是和價格決定機制相關的另一個角度。
比如 @iamaloop 的看法:不存在 Cheap DAI,套利者會搬平各處的價格。 A 參數只會影響 Curve y Pool 里的幣價跟市價齊平后,各個幣百分比的失衡程度。
@sjlee 有類似的表達。 @angelangel0v 提出,套利者沒法因為高的 A 參數就獲得更低的價格。
這三位的看法,簡要概括就是:DAI 的價格是市場供需決定的,A 參數只能決定 Curve y Pool 在不同 DAI 價格點上的深度、決定不了市場價格。
雙方觀點的對峙,其實引出了一個問題:A 參數和市場供需的關係是怎樣的?
A 參數對供給側的重要影響
在某些情況下,A 參數在供給一側有著極其重大的影響,進而是價格決定的最重要變數之一。
在引入供需曲線圖之前,先討論幾點重要的前提假設和基本因素。
其一,Curve 是 Passive LP 模式。 我的判斷是,Passive LP 作為供給方,相對而言更為穩定,即面對變化的行情時,其操作頻度相對較低(“操作” 指平衡地去存取流動性、或是帶有交易屬性的單幣模式存取流動性,“相對” 是相對 Uni V3 的主動管理型 LP 或是 CEX 的做市商)。
其二,Curve LP 的收益很大一部分來自和交易費關係不大的 CRV 代幣獎勵,在 2020 年尤甚,且回報率的絕對值較高。 那麼,面對絕對幅度不大的市場變化時(比如 1~2%),LP 就更加穩定。
以上兩點的共同效果是 Curve LP 更加穩定。
其三,對於部分代幣,Curve 是最大的流動性陣地。 比如 2020 年的 y Pool 曾是 DAI 的最大兌換池子。
以上三點同時成立的話,會使得全市場的供給曲線主要由 Curve Pool 決定。 記住這三點前提,以下便進入供需曲線的討論。
先看全市場供給曲線,A 值影響了曲線的形狀。 A 值越高,價格 1 附近的曲線會 “越平越長”,流動性越充沛。

再看需求曲線,我們先假設在平穩的幣市行情下的曲線 – 需求曲線 1。 當 ETH 出現劇跌時,關閉 CDP 的需求急劇上升,市場需要更多的 DAI,因此需求曲線會向右移動 – 需求曲線 2。
我們觀察供需曲線的交點,可以清晰地看出 A 參數對價格的影響。 A 值越低,對應著新的價格均衡點越高。
可見,如果一個代幣的主要流動性陣地在 Curve,那麼 A 參數對價格決定有著極為重要的影響。
結語
A 參數或多或少地影響了全市場的價格決定,其程度取決於 Curve Pool 代幣獎勵幅度、Curve Pool 的市佔率等因素。
如此重要的參數,很自然地引申出一系列問題。 A 參數的設定機制是怎樣的? 誰來設定,數值的選擇標準等。
進一步,市場不是一成不變的,繼續引申出一系列動態問題。 A 參數什麼時候需要調整? 調整 A 參數在 AMM 公式層面有何影響? 等等
二. 調整 A 帶來的曲線變化及損益
2020 年 4 月 17 日,離 312 已一個多月,DAI 依然是正向脫錨狀態,價格在 1.02 左右。
Michael(Curve 創始人)在推特上發起了一個投票,看大家是否支援把 Compound pool 的 A 參數從 900 調到 400。

49 人參與了投票,但回復者僅一人。 8 個小時后,Michael 把 A 調到了 400,又發了一則推特,0 回復。
在那個當下,能真正參與討論這個議題的,寥寥無幾。 Michael 可能沉浸在一個人的試驗之中,調試參數、觀測、改進,在 Telegram 的只言片語中,我感受到了他的興致和樂趣。
回到這次 A 參數的調整,帶來了日化約 0.1% 的損失。

我的這一篇,就是想講清楚 A 調整了之後,到底意味著什麼? 為什麼會帶來損失?
不同 A 值對應曲線的一個圖示
我挑選了一組實際參數設定,進行圖示呈現。 本文的討論物件是 Curve V1 Pool,曲線公式見 V1 白皮書。
黑色曲線對應的參數為:A = 10 D = 20,000
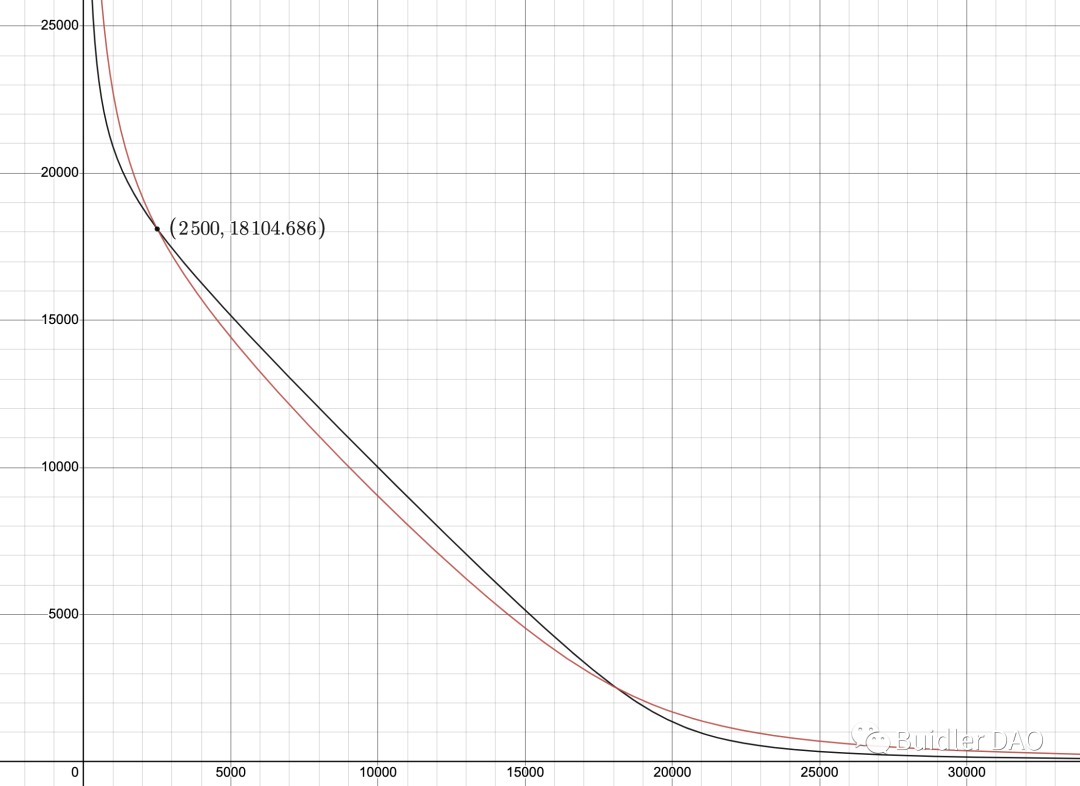
當前池子處於黑色點,X_token、Y_token 的數量分別為 2500 / 18105,價格約為 1X_token = 1.36 Y_token。
此刻將 A 降為 3,曲線將變成紅色線。 這條曲線的參數為:A = 3 D = 19,022
比較紅黑二曲線,很明顯的,黑色曲線中趨近直線的比例更多,這也是 A 之核心作用,A 越大,價格 1 附近的流動性越多; 黑色曲線的 A(10)高於紅色曲線的 A(3)。 相應地,遠離價格 1 的區間的流動性,則是紅色曲線要多過黑色曲線。
在那則推特投票的時刻,DAI 有些脫錨,如果是使用低 A 值的紅色曲線,就能比高 A 值的黑色曲線提供更多的流動性,這也是 Michael 想調整 A 的原因,他希望池子能捕獲更多手續費。
我們再回到將 A 降為 3 帶來的變化,降為 3 的那個瞬間,池子內兩種 Token 的數量並沒有變化,但 D 值發生了變化。 此外,圖中還能看出,當前點的切線斜率發生了變化,曲線形狀亦發生了變化。
以下專門探討這些變化。 切線斜率、曲線形狀的變化,若換一角度考察,會更加直觀。 D 值的變化,則涉及到了池子損益評估的話題。
訂單簿視角來看 A 值調整後的變化
Curve 池子可以從訂單簿的角度去理解。 單個池子,根據其 A、D 參數的不同,對應著在所有價格點上的掛單數量的不同分佈,並且所有的掛單是聯動的、整體性的存在。
上一節的案例里,當 A 從 10 降為 3 的瞬間,可以理解為所有的掛單瞬間做了一次整體性大調整,從黑色的一組掛單集合轉換成了紅色的掛單集合。
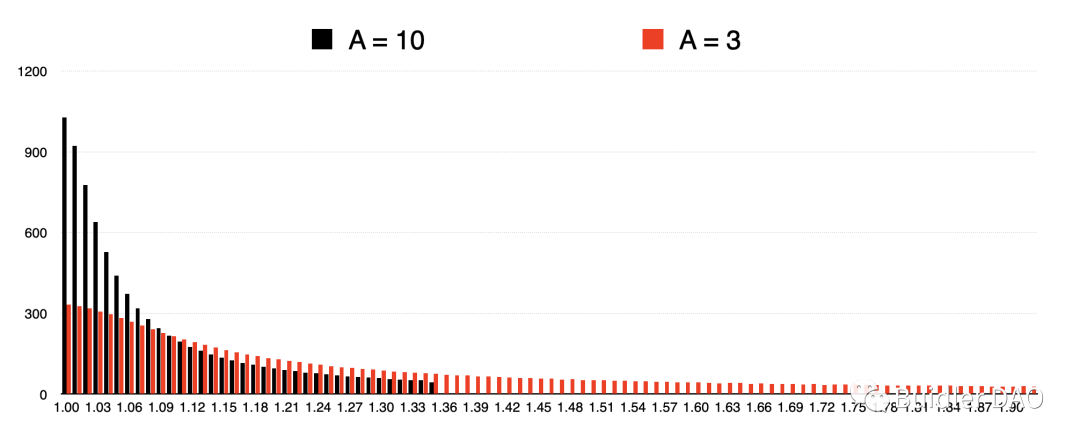
先對上圖做一些基本說明。
橫軸是價格,1.00 代表 1 X_token = [ 1.00 ~ 1.01)Y_token,1.01 代表 1 X_token = [ 1.01 ~ 1.02)Y_token,以此類推。 為了節省空間,我將價格 < 1.00 的掛單略去了。
豎軸表示 Y_token 的數量(即對 X_token 的買單掛單)。 黑色部分在價格 > 1.36 的區間沒有數據,這是因為在黑色曲線上的當前價格是 1.36,> 1.36 意味著 X_token 的更高價賣單掛單。 這張圖僅考察使用 Y_token 進行買入掛單的部分,因此 > 1.36 的部分無數據。
我們看黑紅的對比。 首先,當前價格發生了變化,對應著前一節提到的切線斜率的變化。 A 調整后,當前價格瞬間變動到了 1.92,紅色部分的掛單延展到了 1.92。 也就是說,有一定數量的 Y_token 在 1.36 – 1.92 的價格區間內分批掛出了對 X_token 的買單。
這其實是很奇怪的變化,一個 DEX 的當前價格在沒有 Swap 的情況下,竟然發生了變化。 我們立刻可以想到,這將形成和市場價格的價差,我們假設套利者會瞬間介入把價格打到 1.36。
此外,可以看到從 1.00 – 1.36 的每一個價格點上的掛單數量都有所不同,整體而言,高位掛單的數量更多。 這對應著上一節提到的曲線形狀的變化。
A 調整帶來的損益 – 最直接的計算方式
Michael 的推提及了 Compound Pool A 參數的調低會帶來一些損失('Wipe One Day's Profits')。 在討論背後的數學關係之前,需要先把「損失/損益」定義清楚。

按照最直接的想法,定義損益很簡單,將兩個 Token 的價值折算成 U 或是其中任意一個(X_token 亦或 Y_token),二維轉一維,然後對比 A 調整前後的總價值。 這也是 Michael 提到的『With Impermanent Loss』。
不妨先簡要討論這個意義上的損益。 為求簡化,所有的討論暫且假設手續費 = 0。
還是基於前文一直用的示例,A 調低后,X_token 的暫態價格變高,套利者介入,把價格打回 A 調整前的價格,這便會帶來損失。 道理很簡單,上一節提到,A 調低后,相當於按照高於市場價的價格掛了很多對 X_token 的買單,這些不正常的買單被套利者吃掉,這必然會帶來損失。
從曲線圖上看得會更加清晰。
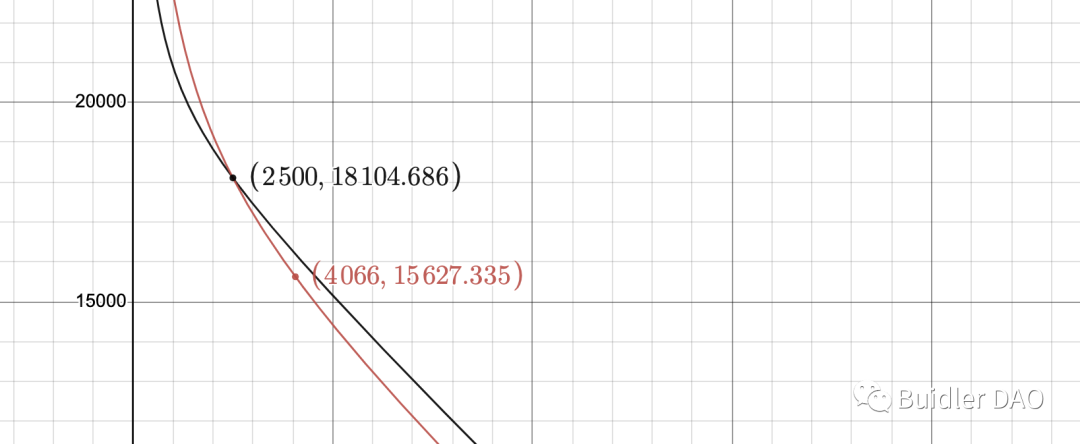
黑色點和黑色曲線是調整前池子的狀態,對應價格為 1.36 。 A 調低后,池子按紅色曲線運行,調低的瞬間,池子價格變成 1.92,套利者介入使得池子的狀態很快從黑色點移到紅色點,對應著 1.36 的價格。
需要比較 A 調整前後的池子總價值,方法比較簡單。
先看 A 調整后的總價值(套利者介入后)。 找出紅色曲線在紅色點處的切線和 Y 軸的交點,即為兩種 Token 按現價折算成單一 Y_token 的數量。
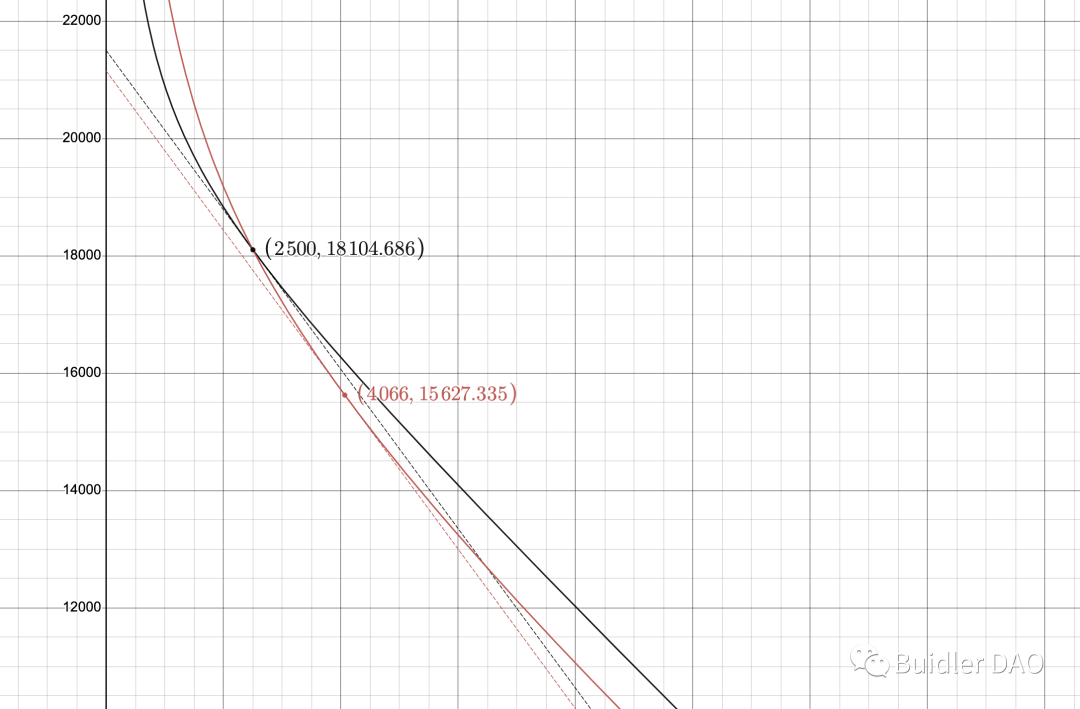
再看 A 調整前的總價值。 找出黑色曲線在黑色點處的切線和 Y 軸的交點。 因為 A 調整前後的價格是一樣的(套利者介入後),因此這條切線和第一步里的切線平行。
顯然,黑色切線與 Y 軸的交點更高,也就是 A 調整前的總價值更高。 A 調低帶來了總價值的損失。
以上討論僅限於 A 調低後的暫態損失,還算簡單。 但若把追蹤時間拉長,想探討後續不同價格走勢下 A 調低所帶來的長期損益,就變得有些複雜。 這取決於價格往更加脫錨的方向去發展、還是回歸完美的錨定,A 調整后的總價值可能會不如不調整 A 的狀態、也有可能會高過。 這裡暫不展開,本文的目的僅在簡要演示一番 A 調整是如何影響到池子總價值的,並不求完整系統的論述。
剔除無常的損益評估
按照兩個 Token 的當前價格折算,也就是考慮進無常,這是最直觀的度量方法,但這種方法較為麻煩。 Curve 引入了另一種獨特的損益評估法,剔除了無常的因素,簡化了計算,在大部分情況下也能夠適用。
這就是 D 值,D 值是 Curve 曲線公式在 A 之外的另一核心參數。 我們在 Curve 官網每個池子裡看到的 Virtual Price 即為根據 D 值計算得出。

D 值,就是當池子價格是 1(完美錨定)的時候,池子內兩種 Token 的總數量。 因為此刻價格是 1,因此可以把兩種 Token 的數量簡單相加。 池子價格等於 1 的點,即為曲線和 x=y 這條直線的交點。

回到前述示例,A 調低以後,很顯然,D 值變小了。 因此,長期來講如果價格能夠恢復錨定的話,D 值的變化能夠反映出因為 A 調整帶來的損失。
我上文使用的示例中,當前價格是 1.36,這其實是比較極端的情況。 我們看 Curve V1 類池子,比如主流的穩定幣/ LSD 池子,價格都不會偏離 1 太多。 在價格接近 1 的時候,無常的影響很小,因此可以直接用 D 值的變化來近似反映損益。
D 值,作為一維的度量衡,且作為池子的參數之一,便於計算、便於追蹤歷史數值,比較適合用來近似地評估損益。
結語
A 參數的調整相當於在訂單簿所有價格點上的掛單的一次重排,改變了當前價格點,改變了 D 值,帶來了損益。
因此,A 參數的一次性大幅調整有一種突兀感,甚至有一種瑕疵感。 白皮書內對 A 的動態管理並無涉及,或許是在 Curve 上線實際運行了一段時間後,Michael 才漸漸認識到了對 A 參數的調整方式需要修正。 在宣佈 Compound Pool A 參數調整完畢的那則推特下,Michael 跟了一句評論。 後續新版本的池子,A 參數的調整改成了一段時間漸變完成的模式。

老池子 A 參數的一次性調整方式僅僅是瑕疵感嗎? 沒這麼簡單,背後還深藏了一個可被攻擊的點。 幸運的是,發現這個脆弱點的是白帽(對協定理解的深度真是天外有天)。 後續會單寫一篇講述這個攻擊方法。
免責聲明:作為區塊鏈資訊平臺,本站所發佈文章僅代表作者及嘉賓個人觀點,與 Web3Caff 立場無關。 本文內容僅用於資訊分享,均不構成任何投資建議及要約,並請您遵守所在國家或地區的相關法律法規。