KZG 受信任初始化對 Danksharding 的實現起著至關重要的作用,本文介紹了受信任初始化的運作原理以及其驗證過程。
原文:How do trusted setups work?(vitalik.ca)
作者: Vitalik Buterin
編譯:雙花 (@doublespending)
校對: ECN
編者註:
數據可用性採樣 (data availability sampling) 是 Dankshading 的關鍵部分,為實現這一密碼協議,需要使用 KZG 儀式對數據可用性證明方案所需要的參數進行初始化。
因此,KZG 受信任初始化是實現 EIP-4844 (proto-danksharding) 和完整版 Danksharding 的重要前提條件。
除此之外,其他密碼學協議如 ZK-SNARKs 領域也需要有受信任初始化階段。
本文介紹了受信任初始化的運作原理以及其驗證過程。
推薦閱讀:
《Vitalik: Proto-Danksharding FAQ》
《分片+ 數據可用性採樣》www.ethereum.cn/sharding-proposal
必要的背景知識:elliptic curves and elliptic curve pairings。
另請參閱:Dankrad Feist's article on KZG polynomial commitments。(中文版:KZG 多項式承諾)
特別感謝 Justin Drake、Dankrad Feist 和 Chih Cheng Liang 的反饋和評審。
許多密碼協議尤其是在數據可用性採樣和 ZK-SNARKs 領域都依賴於受信任初始化。受信任初始化儀式是一個用於生成一批數據的一次性流程。
後續,每次運行某些密碼協議時都必須使用這些數據。生成這些數據需要一些秘密信息;“信任” 來源於這樣一個事實,即必須由某個人或某組人來生成這些秘密,使用秘密來生成數據,然後發布數據並銷毀這些秘密。
然而,一旦生成了數據並銷毀了秘密,儀式創建者就不需要進一步的參與。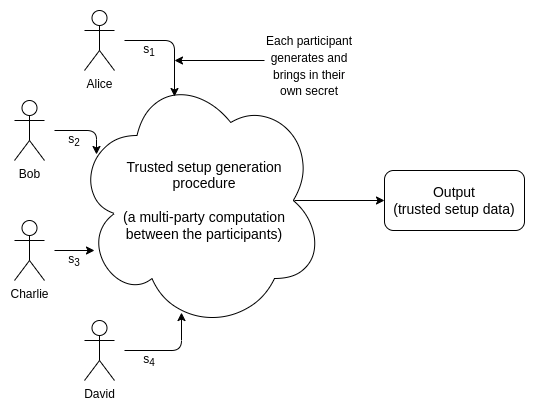
受信任初始化有很多類型。在主流協議中最早使用的受信任初始化的實例是 2016 年的 Zcash 啟動儀式。這個儀式非常複雜,而且需要多輪的通信交互,因此只能有六名參與者。
彼時彼刻,每個使用 Zcash 的人都必須相信六名參與者內至少有一名是誠實的。新式協議一般會使用 powers-of-tau 初始化技術,其遵循 1-of-N 信任模型,N 值通常為數百。
也就是說,數百人一起參與生成數據,只需其中一人是誠實的並且不公開秘密就能保證最終輸出的安全性。實踐上,像這樣的執行良好的受信任初始化通常被認為是 “足夠接近於去信任” 的。
本文將介紹 KZG 初始化如何運作及其工作原理,以及受信任初始化協議的未來。任何精通代碼的人都可以隨意地瀏覽以下代碼實現:https://github.com/ethereum/research/blob/master/trusted_setup/trusted_setup.py.
Powers-of-tau 初始化是怎樣的?
powers-of-tao 初始化由兩系列的橢圓曲線點組成,如下所示: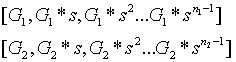
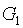 和
和 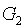 是兩個橢圓曲線群的標準生成元;在 BLS12-381 中,
是兩個橢圓曲線群的標準生成元;在 BLS12-381 中,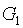 佔用 48 字節(壓縮形式),
佔用 48 字節(壓縮形式),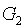 佔用 96 字節。
佔用 96 字節。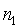 ,
, 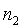 分別是初始化輸出的
分別是初始化輸出的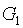 ,
, 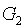 生成點列的長度。一些協議要求
生成點列的長度。一些協議要求 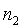 =2,另一些協議要求
=2,另一些協議要求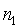 和
和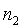 的值都較大,一些協議屬於中間情形(例如,當前的以太坊數據可用性採樣方案要求
的值都較大,一些協議屬於中間情形(例如,當前的以太坊數據可用性採樣方案要求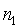 =4096 和
=4096 和 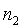 =16)。
=16)。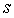 是用於生成點列的秘密值,使用後需要銷毀。
是用於生成點列的秘密值,使用後需要銷毀。
為了對多項式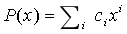 生成 KZG 承諾,我們簡單選取一個線性組合
生成 KZG 承諾,我們簡單選取一個線性組合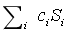 ,其中
,其中  (受信任初始化中的橢圓曲線點列)。
(受信任初始化中的橢圓曲線點列)。
初始化中的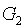 用於驗證我們所承諾的多項式的值;我不會在此討論驗證流程的細節,更多的細節參見 Dankrad 的文章 (https://dankradfeist.de/ethereum/2020/06/16/kate-polynomial-commitments.html)。
用於驗證我們所承諾的多項式的值;我不會在此討論驗證流程的細節,更多的細節參見 Dankrad 的文章 (https://dankradfeist.de/ethereum/2020/06/16/kate-polynomial-commitments.html)。
直觀地說,受信任初始化提供了什麼價值?
從更深層次理解這裡面到底發生了什麼,以及受信任初始化為何能夠提供這些價值。
多項式承諾使用大小為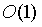 的對象(單個橢圓曲線點)對一段大小為
的對象(單個橢圓曲線點)對一段大小為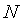 的數據進行承諾。我們可以用簡單的 Pedersen 承諾來做到這一點:
的數據進行承諾。我們可以用簡單的 Pedersen 承諾來做到這一點:
只需將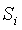 的值設置為
的值設置為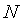 個不相關的隨機橢圓曲線點,然後如前所述對
個不相關的隨機橢圓曲線點,然後如前所述對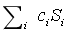 多項式進行承諾。實際上,這正是 IPA 證明所做的。(https://vitalik.ca/general/2021/11/05/halo.html)
多項式進行承諾。實際上,這正是 IPA 證明所做的。(https://vitalik.ca/general/2021/11/05/halo.html)
然而,任何基於 IPA 的證明都需要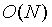 時間來驗證,有一個不可避免的原因:使用基點
時間來驗證,有一個不可避免的原因:使用基點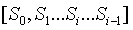 對多項式
對多項式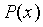 生成的承諾會對應於使用基點
生成的承諾會對應於使用基點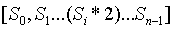 的另外一個多項式。
的另外一個多項式。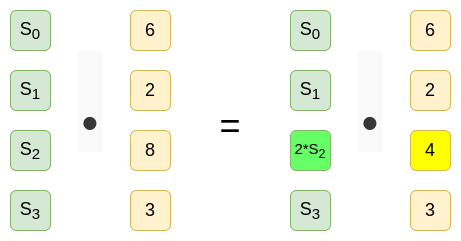
在一組基點下對多項式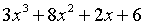 的一個有效承諾等效於另一組基點下對多項式
的一個有效承諾等效於另一組基點下對多項式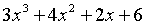 的一個有效承諾。
的一個有效承諾。
如果我們想對某些命題生成基於 IPA 的證明(例如,該多項式在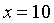 時等於 3826),該證明在基於第一組基點時應當驗證通過,而在基於第二組基點時應當驗證失敗。
時等於 3826),該證明在基於第一組基點時應當驗證通過,而在基於第二組基點時應當驗證失敗。
因此,無論驗證流程如何,都無法避免以某種方式考慮每一個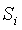 值,因此不可避免地需要
值,因此不可避免地需要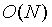 時間。
時間。
然而,如果有受信任初始化的話,點間存在著隱藏的數學關係。可以保證任意兩個相鄰點之間有著相同的因子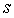 使得
使得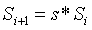 。如果
。如果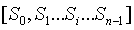 是有效的初始化輸出,“被篡改的輸出”
是有效的初始化輸出,“被篡改的輸出” 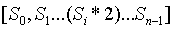 是無效的。
是無效的。
因此,我們不需要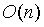 的計算量;相反,我們利用這個數學關係就可以在
的計算量;相反,我們利用這個數學關係就可以在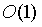 時間下驗證我們需要驗證的任何東西。
時間下驗證我們需要驗證的任何東西。
然而,數學關係必須保密:如果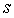 已知,那麼任何人都可以提出一個表示眾多不同多項式的承諾:如果
已知,那麼任何人都可以提出一個表示眾多不同多項式的承諾:如果 是
是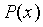 的承諾,那麼它也是
的承諾,那麼它也是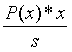 或
或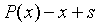 或許多其他多項式的承諾。這將完全破壞所有多項式承諾應用的根基。
或許多其他多項式的承諾。這將完全破壞所有多項式承諾應用的根基。
因此,雖然在某個時間點上必須存在一些秘密值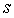 ,讓
,讓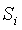 值之間的數學聯繫成為可能,從而實現高效驗證,但是
值之間的數學聯繫成為可能,從而實現高效驗證,但是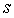 也必須被銷毀。
也必須被銷毀。
多方受信任初始化如何運作?
單個參與者進行初始化是很簡單的:只需選擇一個隨機值 ,並使用
,並使用 值生成一系列橢圓曲線點。但單個參與者的受信任初始化是不安全的:你必須信任某個特定的人!
值生成一系列橢圓曲線點。但單個參與者的受信任初始化是不安全的:你必須信任某個特定的人!
解決方案是多方受信任初始化,其中 “多” 指的是很多參與者:超過 100 人是正常的,對於較小計算量的初始化方案,可能會超過 1000 人。以下是多方 powers-of-tau 初始化的工作原理。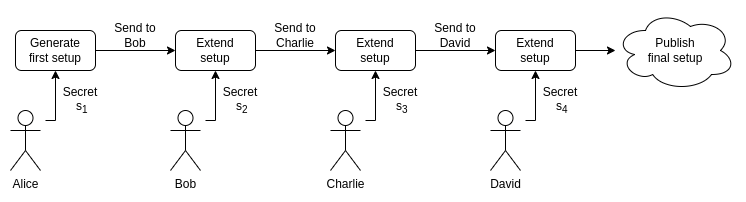
以一個已有的初始化輸出為切入點(注意,你不知道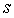 的值,你只知道一系列的橢圓曲線點):
的值,你只知道一系列的橢圓曲線點):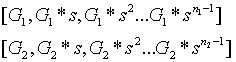
現在,選擇你自己的隨機秘密值 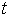 。計算:
。計算: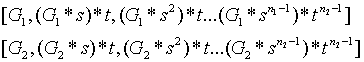
請注意,這相當於: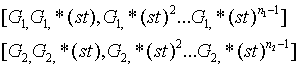
也就是說,您已經創建了一個秘密值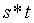 相對應的有效初始化輸出!你永遠不會把你的秘密值
相對應的有效初始化輸出!你永遠不會把你的秘密值 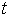 給到之前的參與者,同時之前的參與者也不會把他們的秘密值
給到之前的參與者,同時之前的參與者也不會把他們的秘密值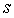 給到你。
給到你。
只要任意一個參與者是誠實的,並且沒有透露他那部分的秘密值,那麼組合起來的秘密值就不會被洩露。
特別地,有限域具有這樣的性質:如果你知道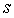 但不知道
但不知道 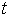 ,並且
,並且 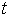 是被安全隨機地生成的,那麼你對
是被安全隨機地生成的,那麼你對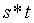 的值一無所知!
的值一無所知!
驗證受信任初始化
為了驗證每個參與者確實參與了受信任初始化,每個參與者都可以提供這樣一個證明,包括 (i) 他們收到的點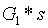 和 (ii)
和 (ii) 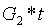 ,其中 tt 是他們引入的秘密值。
,其中 tt 是他們引入的秘密值。
這一系列的證明可用於驗證最後的初始化輸出將所有的秘密值組合起來 (與之相反的是,最後一個參與者只是捨棄了前面的值,並輸出了僅由他自己秘密值生成的初始化結果,他可以自行保留這個秘密值,從而在任何使用該初始化輸出的協議中欺詐)。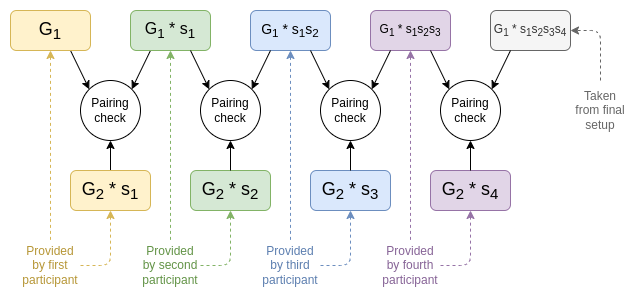
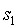 是第一個參與者的秘密值,
是第一個參與者的秘密值,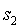 是第二個參與者的秘密值,以此類推。在每個步驟中的配對檢查驗證了每個步驟的初始化輸出確實源自前一步驟初始化輸出以及參與者在當前步驟中已知的新秘密值的組合。
是第二個參與者的秘密值,以此類推。在每個步驟中的配對檢查驗證了每個步驟的初始化輸出確實源自前一步驟初始化輸出以及參與者在當前步驟中已知的新秘密值的組合。
(譯者注:配對的特性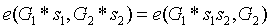 )
)
每個參與者都應該在一些公開可驗證的媒體(例如個人網站、來自其 eth 地址的交易、推特)上披露他們的證據。
請注意,這個機制並不能阻止某些人聲稱參與了某個階段,而實際上是另外的人(假設其他人已經透露了他們的證據),但通常會認為這不成問題:如果有人願意就參與的情況撒謊,他們也會願意就秘密的刪除情況撒謊。只要公開聲稱參與的人中至少有一人是誠實的,那麼初始化就是安全的。
除了上述檢查以外,我們還想驗證初始化中的所有橢圓曲線點的冪次都是正確的(即,它們是相同秘密值的冪)。(譯者注,即橢圓曲線可以表示為序列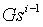 )
)
為此,我們可以進行一系列配對校驗,驗證 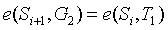 (其中
(其中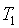 是初始化中
是初始化中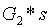 的值)。
的值)。
這驗證了每個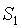 和
和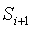 之間的因子與
之間的因子與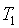 和
和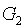 之間的因子相同。然後,我們可以在 G_{2}G2 側執行相同的操作。(譯者註,即驗證
之間的因子相同。然後,我們可以在 G_{2}G2 側執行相同的操作。(譯者註,即驗證 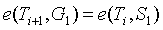 (其中
(其中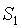 是初始化中
是初始化中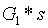 的值)
的值)
然而,這需要很多次配對,成本很高。相反,我們採用隨機線性組合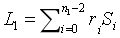 ,及相同線性組合移動一位的結果:
,及相同線性組合移動一位的結果: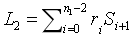 。我們使用單個配對校驗來驗證它們是否匹配得上:
。我們使用單個配對校驗來驗證它們是否匹配得上: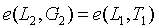 。
。
我們甚至可以將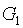 側和
側和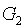 側的校驗過程結合在一起:除瞭如上所述計算
側的校驗過程結合在一起:除瞭如上所述計算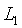 和
和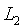 ,我們還計算
,我們還計算 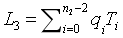 (
(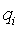 是另一組隨機係數)和
是另一組隨機係數)和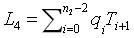 ,然後驗證
,然後驗證 。
。
拉格朗日形式的受信任初始化
在許多用例中,你不太願意使用係數形式的多項式(例如 ,你更願意使用點值形式的多項式(例如
,你更願意使用點值形式的多項式(例如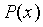 是在域
是在域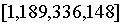 模 337 的值為
模 337 的值為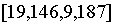 的多項式)。(譯者注:此處的邏輯是,n 次多項式需要 n+1 個點來進行確定,點值形式其實指的是
的多項式)。(譯者注:此處的邏輯是,n 次多項式需要 n+1 個點來進行確定,點值形式其實指的是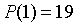 ,
, 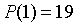 , 如此類推)
, 如此類推)
點值形式有很多優點(例如,您可以在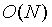 時間內進行多項式的乘法,某些情況下的除法運算),你甚至可以把它用在
時間內進行多項式的乘法,某些情況下的除法運算),你甚至可以把它用在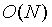 時間內求值。特別地,數據可用性採樣要求 blobs 使用點值形式進行表示。
時間內求值。特別地,數據可用性採樣要求 blobs 使用點值形式進行表示。
為了處理這些情況,通常可以便捷地將受信任初始化轉換為點值形式。這讓你能得到點值(上面的例子中為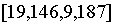 ,並直接使用它們來計算承諾值。
,並直接使用它們來計算承諾值。
使用快速傅里葉變換(FFT)是最為便捷的手段,但是要將曲線點而非數值作為輸入進行傳遞。我將避免在此重複對 FFT 進行詳細的解釋,但這裡有一個實現;FFT 實際上並不難。
受信任初始化的未來
Powers-of-tau 並不是唯一的受信任初始化方案。其他一些(實際上或潛在)值得注意的受信任初始化方案包括:
- 舊版的 ZK-SNARK 協議中使用的更為複雜的初始化方案(例如,參見此處) 有時仍會被使用(特別地,Groth16),因為它驗證成本會比 PLONK 更低。
- 一些密碼協議(例如,DARK) 依賴於隱階群,群中元素不知道進行多少次乘法運算才能得到零元素。目前存在著完全無信任的版本(請參閱:class groups),但目前為止,最高效的版本使用的是 RSA 群(
 的冪 mod
的冪 mod  ,其中
,其中 ,
, 未知)。遵循 1-of-n 信任假設的受信任初始化方案是可能的,但實現起來非常複雜。
未知)。遵循 1-of-n 信任假設的受信任初始化方案是可能的,但實現起來非常複雜。 - 如果/當不可區分混淆變得可行時,許多依賴於它的協議將會涉及:某人創建和發布一個混淆程序,該程序使用內部的隱藏秘密來執行某些操作。這就是受信任初始化流程:創建者需要持有秘密值來創建程序,而且之後需要把秘密值刪除。
密碼學仍然是一個快速發展的領域,受信任初始化的重要性很容易會改變。
採用 IPA 和 Halo 式思想的技術方案可能會被改進到讓 KZG 變得過時和不必要的程度,或者在十年後量子計算機讓基於橢圓曲線的所有方案都變得不可行,屆時我們將不得不使用無需受信任初始化基於哈希的協議。
KZG 改良得更快,或者出現一個依賴於另一種受信任初始化的全新密碼學領域都是有可能的。
在一定程度上,受信任初始化是必要的,重要的是要記住,並非所有受信任初始化都水平相當。176 個參與者比 6 個更好,2000 個更佳。
相比於要求運行一個複雜軟件包,成本小得可以在瀏覽器或手機應用上進行的受信任初始化儀式(例如,ZKopru 初始化就是基於 Web 應用)能夠吸引多得多的參與者。
理想情況下,每個儀式都應當讓參與者運行多個獨立構建的軟件實現,並且運行在不同的操作系統和環境之上,以減少共模故障的風險。
參與者只需一輪交互的儀式(如 powers-of-tau)遠遠優於多輪交互的儀式,這既是因為能夠支持更多參與者,也是因為編寫多個實現會更加簡單。
理想情況下,儀式應該是通用的(一個儀式的輸出能夠支持大量協議)。這些都是我們可以並應當繼續鑽研的事情,以保證受信任初始化盡可能的安全可靠。
免責聲明:作為區塊鏈信息平台,本站所發布文章僅代表作者及嘉賓個人觀點,與 Web3Caff 立場無關。本文內容僅用於信息分享,均不構成任何投資建議及要約,並請您遵守所在國家或地區的相關法律法規。


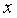 的冪 mod
的冪 mod 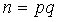 ,其中
,其中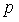 ,
,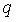 未知)。遵循 1-of-n 信任假設的受信任初始化方案是可能的,但實現起來非常複雜。
未知)。遵循 1-of-n 信任假設的受信任初始化方案是可能的,但實現起來非常複雜。