慢霧安全團隊提醒,在實際應用中需注意審查 Fiat-Shamir 實現的正確性。
作者:Johan, 慢霧安全團隊
封面:Photo by Nicolas Arnold on Unsplash
背景
Frozen Heart “冰心” 漏洞,由 Trail of Bits 團隊命名,其中 Frozen 代表 FoRging Of ZEro kNowledge proofs,Heart 指 Fiat-Shamir transformation 是很多 proof system 的核心。 該漏洞指應用了「弱 Fiat-Shamir」變換,只對證明者的部分消息進行散列而不散列公開資訊(比如參數、公開輸入等),因此出現的安全問題。
下面我們將對這個漏洞進行全面的解析,我們先來談下什麼是 Fiat-Shamir 變換。
Fiat-Shamir 變換
Fiat-Shamir 變換,又叫 Fiat-Shamir Heuristic 或者 Fiat-Shamir Paradigm,是 Fiat 和 Shamir 在 1986 年提出的一個變換,用於將互動式零知識證明協議轉化為非互動式零知識證明協定。 它通過將協定中的隨機挑戰(challenge)替換為哈希函數的輸出來實現這一轉化。 這樣,證明者可以生成證明並將其發送給驗證者,而無需進行交互式的挑戰和回應。
Schnorr 證明是一種互動式零知識證明協定,它允許證明者向驗證者證明某個陳述為真,而不需要透露陳述的細節,同時驗證者可以進行互動式的驗證。 它通常用於證明者知道某個秘密值而不透露該秘密值的情況。
借助 Fiat-Shamir 變換,可以將 Schnorr 互動式證明改造成非互動式。
Schnorr 可以在有限域或橢圓曲線(EC)上實現,技術規範基本相同,只是底層迴圈群不同。 下面我們主要以有限域的形式來描述這兩個過程 [1]:
* 符號說明:
Alice: 協定中的證明者的假定身份
Bob: 協定中的驗證者的假定身份
a | b: a 能整除 b
a || b: a 和 b 的連接 [a, b]: 整數區間,包括 a 和 b
t: Bob 選擇的挑戰的比特位數
H: 安全的密碼哈希函數
p: 一個大素數
q: p-1 的一個大素數因數,即 q | p-1
Zp*: 模 p 的整數的乘法群
Gq: 具有素數階 q 的 Zp* 的一個子群
g: Gq 的生成元
g^d: g 的 d 次方 a mod b:
a 對 b 取模
Fp: 一個由 p 個元素組成的有限域,其中 p 是一個素數
基於有限域的實現
1. 互動式
首先,Alice 計算 A = g^a mod p,其中私鑰 a 取值 [0, q-1],然後公開公鑰 A;
然後,Alice 在不公開 a 的情況下,向 Bob 證明他知道 A 對應的私鑰 a:

如果 check 為 true,那麼就能證明 Alice 知道 a ,原理如下:
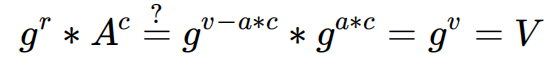
這裡之所以需要由 Bob 生成隨機 c ,是因為如果攻擊者在公開 A 之前知道了這個值,那麼他就可以在不知道真實 a 的情況下偽造證明。 攻擊者偽造(A, V, r)方法如下:

Verifier 收到這三個參數后,代入驗證公式,也是可以通過驗證的。 但是我們注意看這些參數的生成過程,它們與要證明的秘密值 a 沒有任何關係。
2. 非互動式
非互動式的改造也很容易,在互動式的基礎上,把 Bob 隨機生成 c 的過程,改成參數的 Hash 形式:
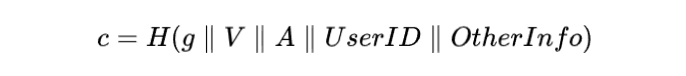
基於橢圓曲線的實現
首先,Alice 計算 A = G x [a],其中私鑰 a 取值 [0, n-1] ,然後公開公鑰 A;
接著,Alice 在不公開 a 的情況下,向 Bob 證明她知道 A 對應的私鑰 a:

如果 check 為 true,那麼就能證明 Alice 知道 a ,原理如下:
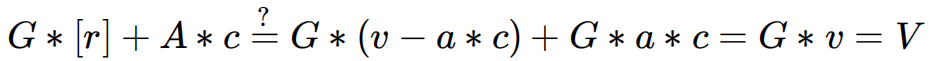
非交互式的實現方式與上述的基於有限域的實現方式相同,就不再贅述。
弱 Fiat-Shamir 變換
上面非交互式的實現過程中,隨機數:
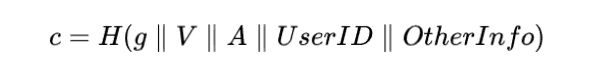
是一種正確且安全的生成方式,但遺憾的是,在早期的一些論文中,並沒有對這個過程進行嚴密地描述,只是簡單地描述成:
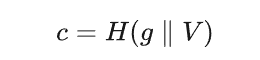
這就存在一個安全問題,我們稱它為弱 Fiat-Shamir 變換,它可以被用於偽造證明,通過預計算 A,欺騙驗證者。
使用以下方法重新建構參數(A, r):

我們可以看到這個 A 變成了一個和 a 無關的參數,代入驗證方程:
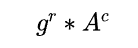
可以等於 V 。
也就是說攻擊者可以在不知道秘密值的情況下通過協議驗證。
還有一些論文 [3] 描述這個過程如下:

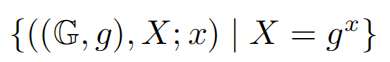
其表達的內容是相同的。
冰心漏洞
Trail of Bits 團隊曾發表文章 [2] 指出 Bulletproofs 和 Plonk 等 ZKP 系統中的 Fiat-Sharmir 實現存在漏洞,使得惡意使用者可為隨機 statement 偽造 proof。
以 Plonk 為例,在證明生成的 Round 2,3,4,5 中,均利用了 Fiat-Shamir 演算法生成隨機數。
在論文 [3] 中調查了許多現代零知識證明系統的開源實現,發現有 36 個使用了弱 Fiat-Shamir 變換,包括 Bulletproofs、Plonk、Spartan 和 Wesolowski 的 VDF 等。 攻擊者可以生成通過驗證的證明,而不需要知道有效的證明秘密。
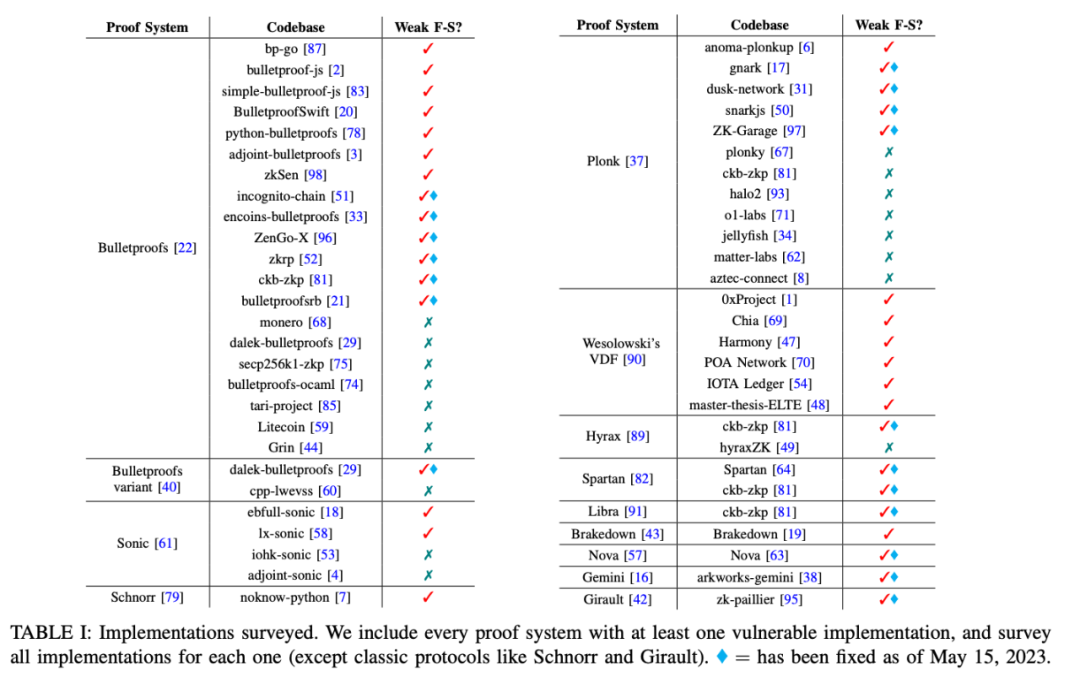
漏洞實例
1. gnark
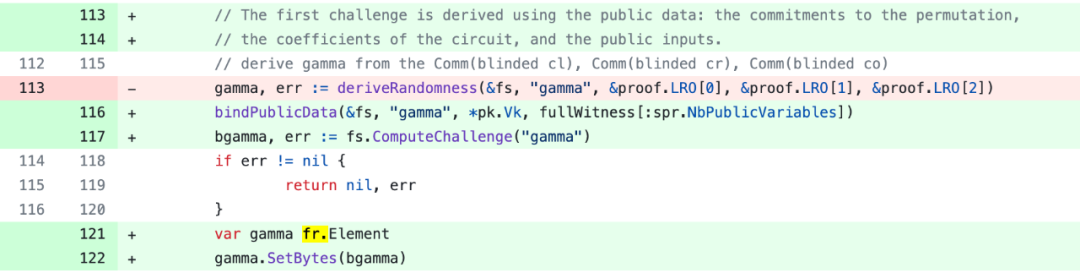

這裡 fs 就是一個 Fiat-Shamir 計算實例,在 Round2 證明計算 z(X)參數時,由於沒有將公共輸入綁定到 challenge,導致了可以偽造證明資訊。
2. snarkjs

同樣由於沒有包含 publicSignals ,導致可以偽造證明資訊。
總結
從披露的內容我們可以看到這個漏洞的通用性和廣泛性,它會對零知識證明造成嚴重危害,在實際應用中我們需要注意審查 Fiat-Shamir 實現的正確性,將公共見證數據也加入到隨機數生成中,避免被攻擊者偽造證明。
最後,感謝領先的一站式數字資產自託管服務商 Safeheron 提供的專業技術建議。
參考文件:
[1]. https://datatracker.ietf.org/doc/html/rfc8235 [2]. https://blog.trailofbits.com/2022/04/13/part-1-coordinated-disclosure-of-vulnerabilities-affecting-girault-bulletproofs-and-plonk/ [3]. https://eprint.iacr.org/2023/691.pdf免責聲明:作為區塊鏈資訊平臺,本站所發佈文章僅代表作者及嘉賓個人觀點,與 Web3Caff 立場無關。 文章內的資訊僅供參考,均不構成任何投資建議及要約,並請您遵守所在國家或地區的相關法律法規。