作為被稱為「下一代」模塊化區塊鏈的 Celestia 備受行業從業者與愛好者關注,這篇文章將論述 Celestia 作為模塊化區塊鍊是如何確保消息檢索結果的完整性的?
— 導讀(Web3Caff 編輯部注)
作者: Hoyt
原用標題: Celestia 如何確保消息檢索結果的完整性
寫作本文的原因:
有感於 Celestia 白皮書中,關於使用'帶命名空間的默克爾樹' 的相關章節,原文寫得比較複雜,我們花了大量的時間去閱讀,查看開源的示例代碼,並和作者反复溝通才最終達成一致。而作為翻譯,我們不能對原文的結構有太大改動,因此,為了使大家理解起來更容易,我們考慮單獨發文,以更簡明的方式向大家介紹相關內容。
問題的由來:
為了實現鏈的容量擴展,Celestia 承諾主權應用將只需下載與其有關的消息(消息和交易的區別是,交易專指改變應用狀態的消息),而不用下載全部消息,但同時,不同應用的消息是打包在同一個區塊裡面的,以實現平等的安全性。
那麼,如何保證當某個應用的執行節點向 Celestia 的存儲節點查詢消息時,存儲節點僅返回所有的相關消息,而且惡意存儲節點無法隱藏特定消息呢(注意這裡跟數據可用性是不同的概念,那個是指不下載所有數據的輕客戶端,如何確信數據可以被驗證節點下載到)。
Celestia 選擇的方案是,將稱為命名空間的應用標識符,插入到消息構成的默克爾樹的節點信息中。這樣做的好處是,可以處理存儲節點隱藏全部相關消息的情況,可以定位被隱藏的消息。另外,無需大幅度修改默克爾樹的生成邏輯,以確保存在一個節點,它的底層葉節點,包含且僅包含某個命名空間的全部消息,且能定位此節點。
而只需要做三件相對簡單的事情,就可以確保默克爾樹的基本特性,不發生變化:首先,生成消息的默克爾樹之前,先按命名空間將消息分組歸併在一起,確保不同命名空間的消息沒有穿插,且命名空間是排好序的。其次,修改生成默克爾樹時使用的哈希函數,以便命名空間信息被包含進節點信息(因為非葉節點,就只有哈希這唯一信息)。第三,檢查默克爾樹時,額外檢查排序是否無誤。
生成帶命名空間的默克爾樹:
前面我們說了,跟通用的默克爾樹邏輯相比,只有生成節點的哈希的函數不同。具體來說,就是在原哈希函數之上,又包裹了一層,使得節點哈希變成形如'minNs|maxNs|原哈希' 的形式,minNs 和 maxNs 分別是此節點所有子節點中,最小和最大的命名空間。
容易看出,對葉節點有 minNs = maxNs,因為它只包含一條消息,只能有一個命名空間。默克爾樹是二叉樹,且我們已對消息做了排序,所以對非葉節點有 minNs 等於左子節點的 minNs,maxNs 等於右子節點的 maxNs。
另外,請注意原哈希函數會把子節點的整個哈希作為輸入,也就是說命名空間也參與哈希計算,因此不能隨意寫,否則樹根哈希會跟區塊裡的記錄不一致,就很容易看出數據無效。下圖是一個帶命名空間的默克爾樹的示意圖(已經按層級優先方式對節點進行了編號 R1、H2...H15):
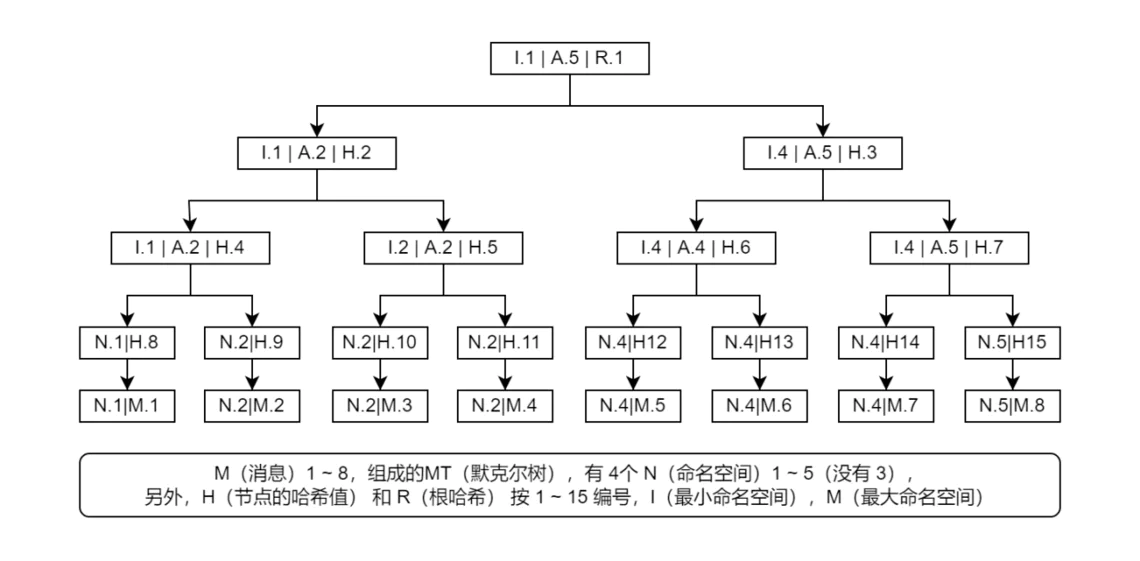
證明消息的完整性:
首先,需要證明返回的某條消息,確實是在消息樹中,這個就是普通默克爾包含證明所作的事情。因此,當存儲節點返回一條消息時,它同時返回此消息的默克爾包含證明。假定返回消息 M0 到 Mn,那會同時返回對應的默克爾包含證明 P0 到 Pn。
我們需要說明,存儲節點可以不返回某條消息,但無法對消息構成的默克爾樹進行變動,因為那會導致樹根哈希變化,數據失效。現在我們來看漏消息的情況,首先我們的消息是按命名空間歸併在一起的,所以如果某個命名空間,在它所有消息的中間漏了消息,那任何一個默克爾證明都可以看出,消息不連續,就沒必要進一步討論了。
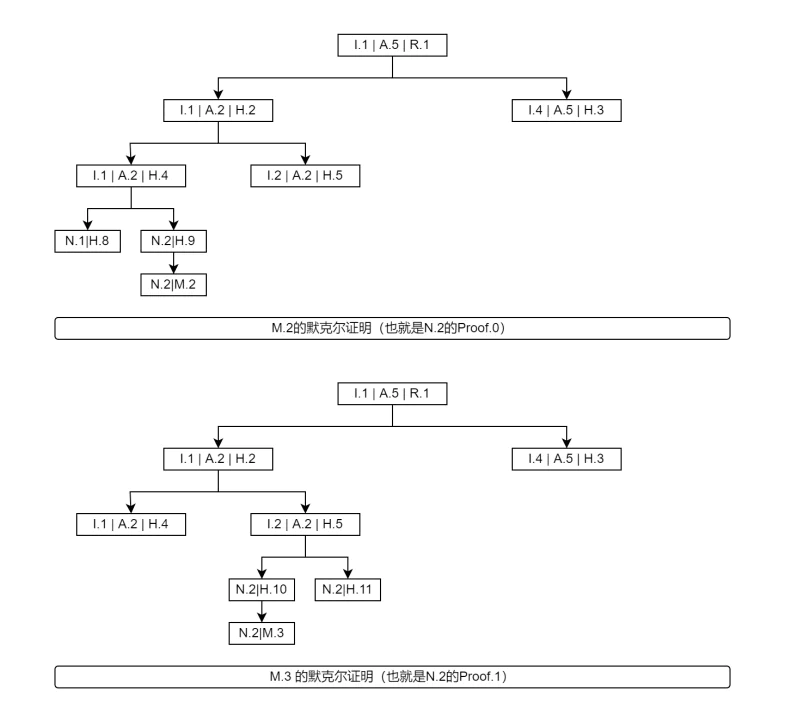
我們看開頭或者結尾漏消息的情況,兩種情況類似,我們以開頭為例。比如 N.2 的第一條消息 M.2 漏了,那它對應的 P.0 也不會發出來,那麼這時候,從查詢者的角度看,原來的 P.1(即 M.3 的默克爾證明),現在是第一個證明,它反正就檢查第一個證明。
下圖,我畫出了 P.0 和 P.1 的具體內容,我們比較它們的差別,就發現 M.2 左側的節點,命名空間都小於 M.2 的命名空間,而 M.3 左側有一個節點 H.4,它的 maxNs 是 A.2 等於 M.3 的命名空間 N.2,這個 A.2 的來源,就是存儲節點隱藏起來的 M.2(參考 P.0 的圖)。這樣一來,執行節點就發現異常了。
那如果某個命名空間全部的消息都被隱藏呢。我們規定,當指定命名空間的消息不存在時,返回一個葉節點的默克爾證明,這個葉節點有 minNs 大於目標命名空間,但它左側所有節點的 maxNs 都小於目標命名空間(按照上圖,如果我們假定 N.2 是空的,那麼應該返回 M.5 的默克爾證明)。
那麼,當存儲節點隱藏了整個命名空間時,必然,根據具體返回的節點的位置(比如它返回 M.5 的話,其實相當於開頭漏消息。那麼它也可能返回 M.8 的默克爾證明),它或者左側會出現一個 maxNs 大於等於目標命名空間的節點(H.14),或者(比如返回 M.1 的默克爾證明)右側會出現一個 minNs 小於等於目標命名空間的情況(H.9)。這樣執行節點也能發現問題。綜上所述,存儲節點不可能隱藏消息而不被發現。
結語:
本文複述了 Celestia 白皮書中,關於多應用場景下(類似分片或側鏈),對抗惡意存儲節點的部分內容。現在 Celestia 測試網已經上線,但目前更多是展示了對輕節點的支持,以及對消息分組的可行性。
白皮書裡面,第三章、第四章都有提到更多關於應用主權或者分片的內容,比較偏概念,針對真實公網環境來說,具體是怎麼實現的,目前還看得不是很清楚。而擴容問題,顯然是整個區塊鏈領域近期最關注的目標。
所以,我們之後也會特別關注 Celestia 在支持獨立應用方面的進展,究竟怎麼跟 L2 或者說其它'區塊鏈模塊' 結合起來,做到實用的功能,並提高鏈上容量,我們將拭目以待。
免責聲明:作為區塊鏈信息平台,本站所發布文章僅代表作者及嘉賓個人觀點,與 Web3Caff 立場無關。本文內容僅用於信息分享,均不構成任何投資建議及要約,並請您遵守所在國家或地區的相關法律法規。













