以太坊已經轉向以 rollup 為中心的路線圖。
原文:The Hitchhiker's Guide to Ethereum(Delphi Digital)
作者: Jon Charbonneau
編譯: zCloak Network
原用標題(譯後):以太坊漫遊指南(上篇)
封面:William Tempest(Ethereum)
主要觀點
- 以太坊是唯一一個旨在建立可擴展、並將結算和數據可用性層統一的主要協議。
- Rollups 在利用以太坊安全性的同時擴展了計算能力。
- 所有的道路最終都通向中心化生成區塊、去中心化和無需信任的區塊驗證以及抗審查。
- 諸如出塊者-區塊打包者分離和弱無狀態等創新,形成了(創建和驗證)權力分離,以實現在不犧牲安全性或去中心化情況下的可擴展性。
- MEV(礦工攫取的價值)現在處於核心重要位置—— 許多設計都是為了減輕其危害和防止其中心化傾向。
- Danksharding 結合了多種前沿研究途徑,為以太坊以 rollup 為中心的路線圖提供所需的可擴展基礎層。
- 我確實期待 Danksharding 在我們的有生之年得以實現。
目錄
| 引言 |
| 第一部分:通往 Danksharding 之路 |
| 1) 原始數據分片設計——獨立分片出塊者 |
| 2) 數據可用性取樣 |
| 3) KZG 承諾 |
| 4) KZG 承諾 vs. 欺詐證明 |
| 5) 協議內提議者-構建者分離 |
| 6) 抗審查清單(crList) |
| 7) 二維 KZG 方案 |
| 8) Danksharding |
| 9) Danksharding – 誠實多數驗證 |
| 10) Danksharding – 重構 |
| 11) Danksharding – 惡意多數安全與隱私隨機抽樣 |
| 12) Danksharding – 主要收穫 |
| 13) Danksharding – 區塊鏈可擴展性的限制 |
| 14) Proto-danksharding (EIP-4844) |
| 15) 多維 EIP-1559 |
| Part II – 歷史和狀態管理 |
| 1) Calldata Gas 成本降低與總 Calldata 限制(EIP-4488) |
| 2) 在執行客戶端中約束約束歷史數據(EIP-4444) |
| 3) 恢復歷史數據 |
| 4) 弱無狀態 |
| 5) Verkle Tries |
| 6) 狀態數據不可用 |
| 第三部分– MEV |
| 1) 當前的 MEV 供應鏈 |
| 2) MEV-Boost |
| 3) 委員會驅動的 MEV 均勻分配 |
| 4) 單槽最終確定性 |
| 5) 單個秘密領袖選舉 |
| 第四部分– 合併:工作原理 |
| 1) 合併後的客戶端 |
| 2) 合併後的共識 |
| 結束寄語 |
引言
自從 Vitalik 說今天出生的人有 50-75% 的機會活到 3000 年,而他希望能長生不老,我就對合併的時機持懷疑態度。但管他呢,讓我們找點樂子,向前看看以太坊雄心勃勃的路線圖吧。

這不是一篇速成文。如果你想對以太坊雄心勃勃的路線圖有一個廣泛而細微的了解,請給我一個小時的時間,我將為你節省幾個月的工作量。
以太坊的研究有很多值得關注的地方,但所有的一切最終都會編織成一個總目標——不犧牲去中心化驗證的可擴展計算。
儘管在區塊鏈中字母"C "(譯者註:“中心化” 單詞的首字母)是可怕的,但 Vitalik 仍在其著名的《Endgame》一文中承認,需要一些中心化來進行擴展。我們只是需要通過去中心化和無需信任的驗證來控制這種中心化的權力,沒有任何妥協可言。
特定的行為主體將為 L1 和基於 L1 的東西構建區塊。以太坊通過簡單的去中心化驗證保持了令人難以置信的安全性,而 rollups 則從 L1 繼承其安全性。以太坊同時提供了結算和數據可用性,以允許 rollup 擴展。這篇文章中的所有研究最終都是為了優化結算和數據可用性這兩個角色,同時使得完全驗證一條區塊鏈比以往更容易。
第一部分:通往 Danksharding 之路
希望你聽說過以太坊已經轉向以 rollup 為中心的路線圖,它不再有執行分片,而是將為需要大量數據的 rollup 進行優化。這將通過以太坊計劃的數據分片或 Celestia 計劃的大區塊來實現。
共識層不解釋分片數據,它只有一個任務,即確保數據可用性(Data Availability)。
接下來我將假設你熟悉一些基本概念,如 rollup、欺詐證明、零知識證明,以及假設你明白為什麼數據可用性這麼重要。
最初的數據分片設計(分片 1.0)—— 獨立的出塊者
該部分描述的設計已經不復存在,但仍是有價值的內容。為了簡單起見,將其稱為"分片 1.0"。
64 個分片區塊中的每一個都有各自獨立的出塊者和委員會,它們在驗證者集中被輪換分配到每個分片區塊,他們各自驗證自己的分片數據是可用的,所以最初這依賴於每個分片驗證者集中的誠實多數完整地下載數據,並不是現在使用的數據可用性抽樣。
最初的設計帶來了不必要的複雜性、更糟糕的用戶體驗和攻擊方法,且在分片之間重排(輪換)驗證者是非常麻煩的。
如果不引入非常緊密的同步假設,就很難保証投票將在單個時間槽內完成。信標區塊(Beacon Block)的出塊者需要收集所有獨立委員會的投票,而這可能會有延遲。
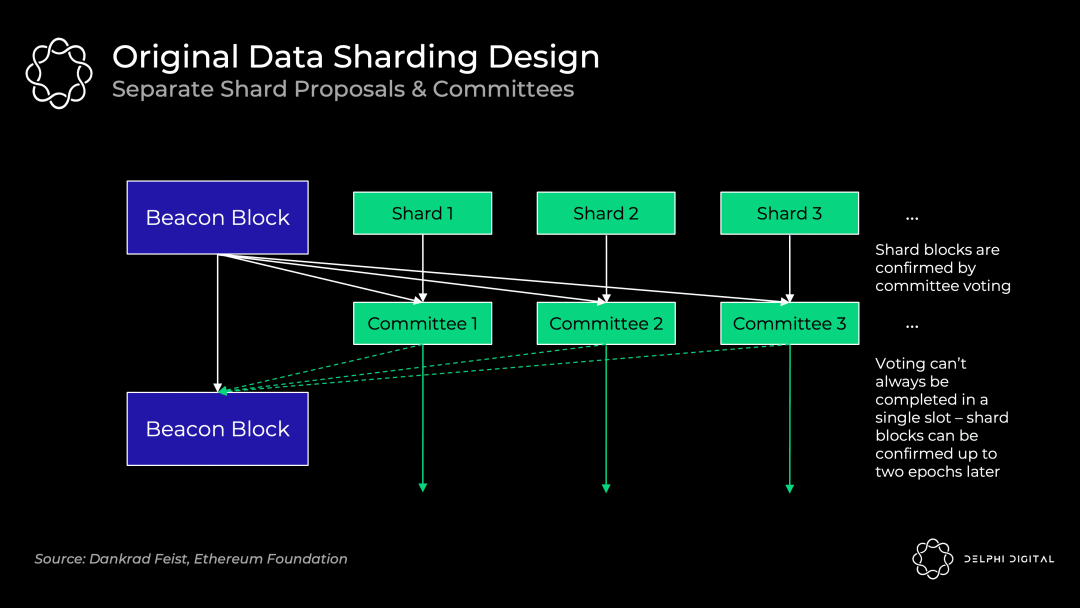
有別於分片 1.0,Danksharding 則完全不同。驗證者進行數據可用性抽樣以確認所有的數據都是可用的(不再有單獨的分片委員會)—— 一個專用的創建者用信標區塊創建一個大區塊,並將所有分片數據一起確認。因此,出塊者-區塊打包者分離(PBS:Proposer-builder Separation)是 Danksharding 保持去中心化的必要條件(一起構建大區塊會佔用大量資源)。

數據可用性採樣
Rollups 會發布大量的數據,但我們不希望它給節點帶來下載所有數據的負擔。高資源需求會損害去中心化。
然而,數據可用性採樣允許節點(甚至輕客戶端)在無需要下載所有這些數據的情況下,輕鬆、安全地驗證它們都是可用的。
- 樸素的解決方案:從區塊中檢查出一堆隨機的數據塊。如果這些塊都沒有什麼問題,就可以簽出。但是,如果你錯過了將你所有的 ETH 交給 Sifu 的那筆交易呢?如此資金就不再是安全的了。
- 聰明的解決方案:先對數據進行糾刪編碼,使用 Reed-Solomon 代碼擴展數據,即數據被插值為多項式,然後在其它的一些位置求值。這很拗口,所以讓我們來解讀一下。
首先上一堂簡單的數學課:
多項式是任何有限數量的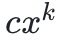 形式的項的求和表達式,其階是最高的指數,例如
形式的項的求和表達式,其階是最高的指數,例如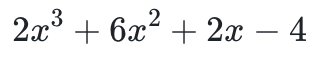 。是一個三階的多項式。你可以基於任意包含 d +1 個坐標的多項式來重構任意的 d 階多項式。
。是一個三階的多項式。你可以基於任意包含 d +1 個坐標的多項式來重構任意的 d 階多項式。
舉個具體的例子:我們有四個數據塊(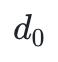 到
到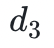 ),這些數據塊可以被映射到多項式 f(X)在給定點的值上,例如 f(0) = ,現在你找到了貫穿這些值的最小階多項式,也就是說基於這四個塊我們可以得到三階多項式。然後,我們可以通過再增加位於同一個多項式上的另外四個值(
),這些數據塊可以被映射到多項式 f(X)在給定點的值上,例如 f(0) = ,現在你找到了貫穿這些值的最小階多項式,也就是說基於這四個塊我們可以得到三階多項式。然後,我們可以通過再增加位於同一個多項式上的另外四個值(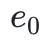 到
到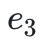 )來擴展該數據。
)來擴展該數據。

多項式的關鍵屬性是我們可以通過任意四個點重構它,但不局限於我們最初使用的四個數據塊。
現在讓我們回到數據可用性抽樣—— 我們只需要確定被糾刪編碼的數據有任意的 50%(4/8)是可用的,如此即可重構整個區塊。
正因如此,攻擊者必須隱藏超過 50% 的區塊才能成功地欺騙數據可用性抽樣節點,使其認為數據是可用的,但實際上並不是。
在多次成功的隨機採樣之後,數據可用性<50% 的概率是非常小的。如果我們成功採樣被糾刪編碼的數據 30 次,可用性<50% 的概率是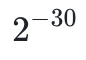
KZG 承諾
現在我們已經做了一堆數據可用性隨機採樣,且這些數據都是可用的。但還有一個問題—— 數據是否被正確的糾刪編碼?不然有可能區塊生成者在擴展區塊時只是添加了 50% 的無用數據,那我們的採樣就是毫無意義的。在這種情況下,我們無法重構數據。
通常,我們只是通過使用 Merkle 根來承諾大量的數據,這對於證明在一個集合內包含一些數據來說是非常高效的。
但我們還需要知道的是,所有的原始數據和擴展數據都位於同一個低階多項式上,而 Merkle 根不能證明這一點。所以如果使用 Merkle 根方案,就還需要欺詐證明,以防出現錯誤的驗證。
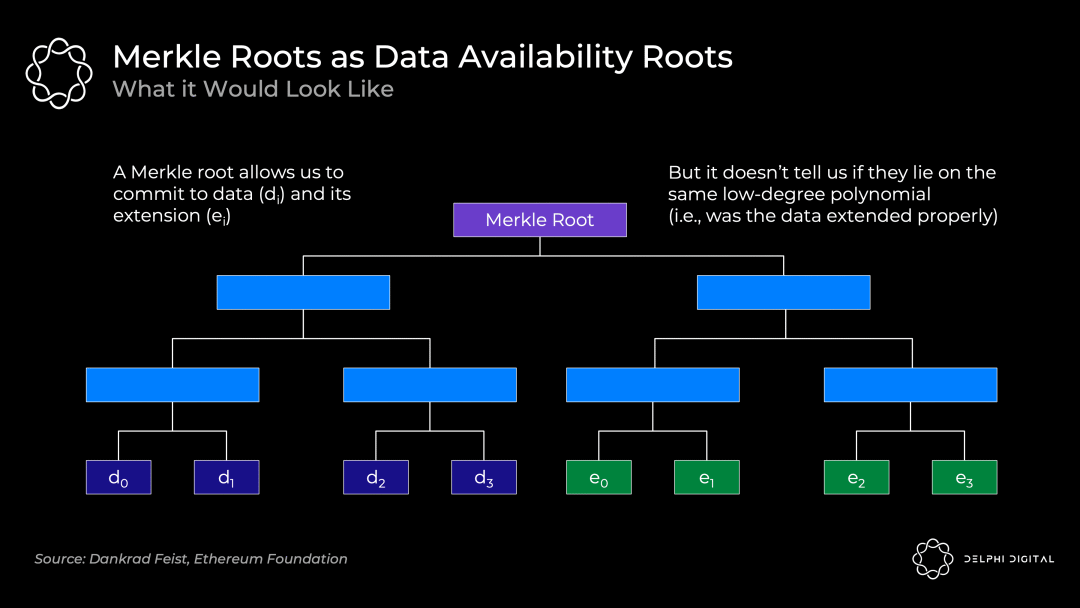
開發人員正從兩個方向來處理這個問題:
- Celestia 走的是欺詐證明路線。該路線需要有人觀察,如果區塊被錯誤地糾刪編碼,這些人會提交一個欺詐證明來提醒大家。這需要標準的誠實少數假設和同步假設(即,除了有人給我發送欺詐證明,還需要假設我是連接到網絡的,並將在一個有限的時間內收到這個欺詐證明)。
- 以太坊和 Polygon Avail 正在走一條新路線—— KZG 承諾(也叫做 Kate 承諾),它移除了欺詐證明安全性對誠實少數和同步假設的需要。
當然也存在其它的解決方案,但它們並沒有被積極的使用。例如,可以使用零知識證明,但目前在計算上零知識證明是不切實際的,然而它有望在未來幾年內取得極大的改善,所以以太坊很可能會在未來轉向 STARKs,因為 KZG 承諾不具備抗量子計算攻擊的能力。

回到 KZG 承諾,它們是一種多項式承諾方案。
承諾方案只是一種可證明承諾某些值的加密方式。最好的比喻是把一封信放在一個上了鎖的盒子裡,然後把它遞給別人。這封信一旦放進去就不會發生改變,但可以用鑰匙打開並證明確實有這樣的一封信。你對這封信作出承諾,而鑰匙就是證明。
在我們的案例中,我們將所有的原始數據和擴展數據映射到一個 X,Y 網格上,然後找到貫穿它們的最小階多項式(這個過程被稱為 Lagrange 插值)。該多項式即是證明者要承諾的:

以下是主要要點:
- 我們有一個"多項式" f(X)
- 證明者對該多項式做出"承諾" C(f)
- 這依賴於具有可信設置的橢圓曲線密碼學
- 對於這個多項式的任意"值" y = f(z),證明者可以計算出一個"證明" π(f,z)
- 給出承諾 C(f),證明π(f,z),任意位置 z,以及多項式在 z 處的值 y,驗證者可以證實的確 f(z)=y
- 也就是說,證明者將這些零散的信息交給任意驗證者,該驗證者可以證實某個點的值(代表源數據)正確地位於被承諾的多項式上
- 這就證明了原始數據被正確地擴展了,因為所有的值都位於同一個多項式上
- 注意,驗證者不需要多項式 f(X)
- 重要屬性—— 有 O(1) 的承諾大小,O(1) 的證明大小,以及 O(1) 的驗證時間。即使對證明者來說,承諾和證明生成也只是 O(d) 的(其中 d 是多項式的階)。
- 也就是說,即使 n(X 中值的數量)增加(即數據集隨著分片 Blob 的增大而增大),承諾和證明的大小也保持不變,驗證需要的工作量也是恆定的
- 承諾 C(f) 和證明π(f,z) 都只是配對友好曲線(BL12-381)上的一個橢圓曲線元素。在這種情況下,它們各自只有 48 字節(真的很小)
- 因此,證明者承諾的大量原始和擴展數據(表示為多項式上的許多值)仍然只有 48 字節,而證明也將只有 48 字節
- 總而言之,是高度可擴展
KZG 根(一個多項式承諾)將類似於 Merkle 根(一個向量承諾):
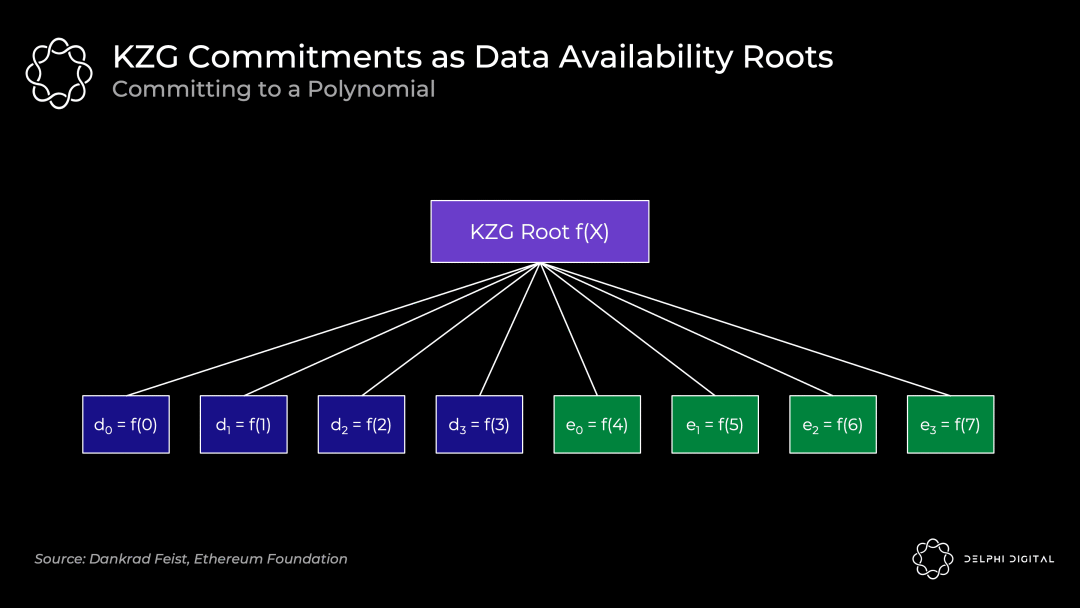
原始數據是多項式 f(X) 在 f(0) 到 f(3) 位置的值,然後我們通過在 f(4) 到 f(7) 位置計算出多項式的值以擴展它。所有的點 f(0) 到 f(7) 都保證是在同一個多項式上。
總之,數據可用性抽樣允許我們檢查被糾刪編碼的數據是可用的。KZG 承諾向我們證明了原始數據被正確地擴展,並承諾所有多項式上的數據。

好了,今天的代數就講到這裡。
KZG 承諾 vs. 欺詐證明
我們已經了解了 KZG 的工作原理,現在來比較一下這兩種方法。
KZG 的缺點是它不是抗量子的,且需要一個可信設置。這些並不令人擔憂,因為 STARKs 提供了一個抗量子的替代方案,而可信設置(是開放參與的)只需要一個誠實的參與者。
KZG 相較欺詐證明場景的優勢是其延遲更低(GASPER 無論如何不會有快速最終確定性),而且它在沒有引入欺詐證明中固有的同步假設和誠實少數假設的情況下,確保了可以適當的進行糾刪編碼。
然而,考慮到以太坊仍然會在區塊重構中再次引入這些假設,所以實際上並沒有消除這些假設帶來的影響。數據可用性層,總是需要為區塊最初可用但隨後因節點需要相互通信而將區塊重新構建起來的情況進行規劃。這種重構需要兩個假設:
- 有足夠多的(輕或全)節點對數據進行採樣,以至於它們共同擁有足夠多的數據可以拼湊起來。這是一個相當弱的、不可避免的誠實少數假設,所以不是什麼大問題。
- 重新引入同步假設,使節點能在一定時間內進行通信,以便將這些數據重新組合起來。
以太坊驗證者在原始的 Danksharding 方案中(Proto)需要完整地下載分片二進制數據塊(Blob: binary large object),而在 Danksharding 中它們只會進行數據可用性抽樣(下載指定的行和列),Celestia 則要求驗證者下載整個區塊。
需要注意的是,在任何一種情況下重構都需要同步假設。如果區塊僅部分可用,則全節點必須與其它節點進行通信以將區塊拼湊出來。
如果 Celestia 想從要求驗證者下載全部的數據轉變為只執行數據可用性抽樣(儘管這種轉變目前還沒有計劃好),那麼 KZG 的延遲優勢就會顯現出來。然後他們也需要實現 KZG 承諾,因為等待欺詐證明意味著將顯著增加區塊間隔,並且意味著驗證者投票給編碼錯誤區塊的危險性將特別高。
為深入探討 KZG 承諾的工作原理,我推薦下以下閱讀內容:(見文尾鏈接)
- [1](相對容易理解的)橢圓曲線密碼學入門
- [2] 探索橢圓曲線配對—— Vitalik
- [3] KZG 多項式承諾—— Dankrad
- [4] 可信設置是如何工作的——Vitalik
協議內出塊者-區塊打包者分離
出塊者-區塊打包者分離(PBS: Proposer-Builder Separation)
今天的共識節點(礦工)和合併後的共識節點(驗證者)擔任兩個角色:他們構建區塊,然後將區塊提交給將驗證區塊的共識節點。礦工在前一個區塊上構建以進行"投票",合併之後,驗證者將直接投票決定區塊是否有效。
PBS 將這個過程拆分,它明確地創建了一個新的協議內區塊打包者角色。特定的區塊打包者把區塊放在一起,並投標出塊者(驗證者)選擇他們的區塊。這對抗了 MEV 的中心化力量。
回顧 Vitalik 的《Endgame》—— 所有的道路都通向基於無需信任和去中心化驗證的中心化區塊生成。PBS 對此進行了編碼。我們需要一個誠實的區塊打包者來為網絡的活性和抗審查服務(這兩點都是為了保持一個有效的市場),驗證者集需要誠實多數假設。PBS 使出塊者的角色盡可能簡單,以支持驗證者的去中心化。
區塊打包者獲得優先的費用小費,並且可以提取任何 MEV。在一個有效的市場中,有競爭力的區塊打包者會出價到他們能從區塊中提取的全部價值(其中會減去他們的攤銷成本,如強大的硬件等)。所有的這些價值都會滲透到去中心化的驗證者集—— 這正是我們想要的。
確切的 PBS 實現仍在討論中,但雙槽 PBS 可能看起來像這樣:
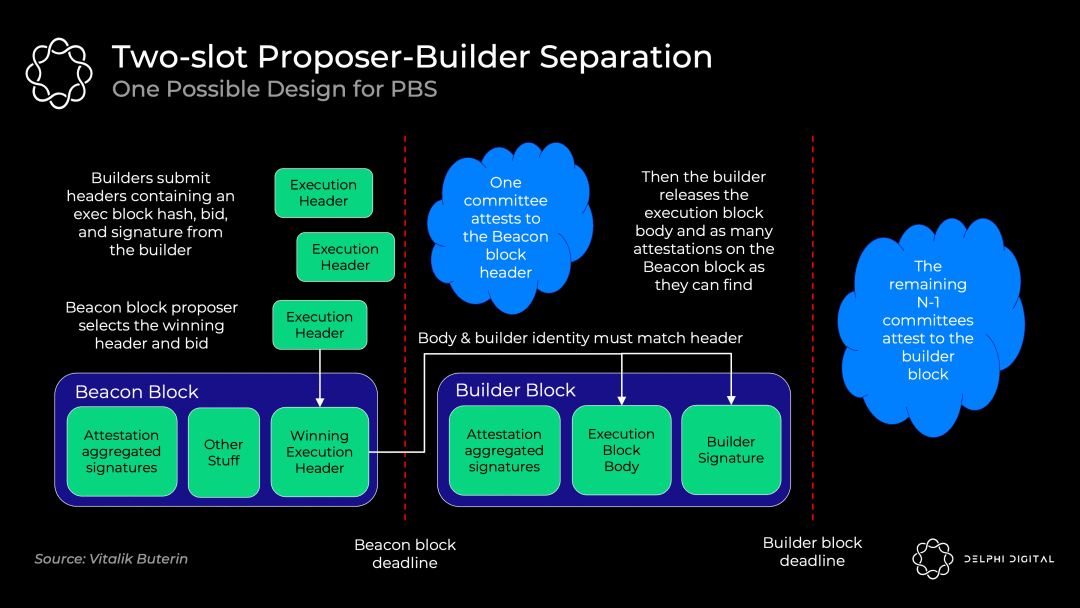
- 區塊打包者對區塊頭和他的出價一起進行承諾
- 信標區塊出塊者選擇獲勝的區塊頭和投標,並將無條件得到中標費,即使區塊打包者未能生成區塊體。
- 證人委員會確認獲勝的區塊頭
- 區塊打包者披露獲勝的區塊體
- 不同的認證人委員會選出獲勝的區塊體(如果中標的區塊打包者不出示區塊體,則投票證明該區塊體不存在)
使用標準 RANDAO 機制從驗證人集中選出出塊者,然後使用一個可以確保在區塊頭被委員會確認之前不會披露完整區塊體的承諾-披露方案。
承諾-披露方案效率更高(發送數百個完整的區塊體可能會超出 p2p 層的帶寬),且還可以防止 MEV 盜取。如果區塊打包者提交它們的完整區塊,則另一個區塊打包者可以觀察到並找出策略與之合併,進而迅速發布一個更好的區塊。此外複雜的出塊者可以檢查並複制使用的 MEV 策略,而無需補償對區塊打包者。如果這種 MEV 盜取行為成為一種均衡,那麼它將激勵區塊打包者和出塊者合併。這就是為什麼我們要用承諾-披露方案來避免這種情況。
在出塊者選擇了獲勝的區塊頭後,委員會對其進行確認,並將其固定在在分岔選擇規則中。然後獲勝的區塊打包者會公佈它們獲勝了的完整的"區塊打包者區塊" 體。如若公佈即及時,下一屆委員會將會對該"區塊打包者區塊" 體進行認證;如若公佈不及時,區塊打包者仍需向出塊者支付全額標價(並失去了所有的 MEV 和費用)。這種無條件的支付不再需要出塊者信任區塊打包者。
延時是這種"雙槽" 設計的缺點。合併後的區塊將有一個固定的 12 秒,所以如果我們在這裡不想引入任何新的假設,那麼我就需要一個 24 秒的完整區塊時間(兩個 12 秒的插槽)。每槽 8 秒(16 秒區塊時間)似乎是一個安全的妥協,不過研究正在進行中。
抗審查清單(crList)
不幸的是,PBS 增強了區塊打包者審查交易的能力。也許區塊打包者只是不喜歡你,所以他們忽略你的交易;也許他們的工作能力很強,以至於其它打包者都放棄工作了;也可能他們會對區塊漫天要價,只是因為真的很不喜歡你。

抗審查清單對以上這些權力進行檢查。具體的實現方式仍然是一個開放的設計空間,不過"混合 PBS "似乎是最受歡迎的,即出塊者指定一個它們在存儲池中看到的所有符合條件的交易列表,區塊打包者將強制包含它們(除非區塊已滿):
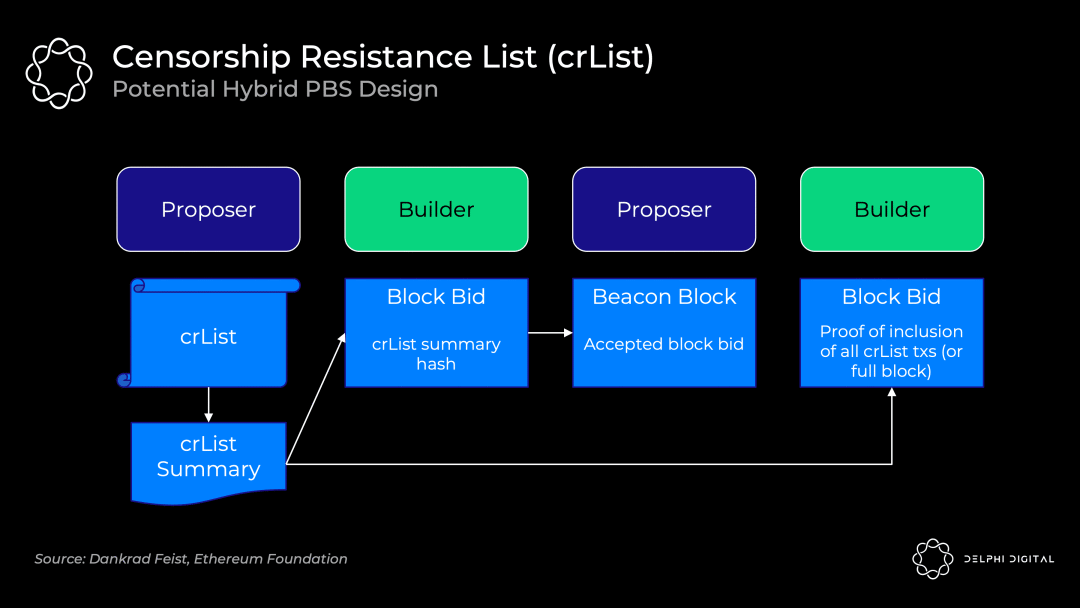
- 出塊者發布一個抗審查清單和包含所有符合條件的交易的抗審查清單摘要
- 區塊打包者創建一個被提議了的區塊體,然後提交投標,其中包括抗審查清單摘要的哈希,以證明他們已看到該提議區塊體
- 出塊者接受獲勝區塊打包者的出價和區塊頭(此時出塊者還沒有看到區塊體)
- 區塊打包者發布他們的區塊和一個可以證明他們已經包含了抗審查清單中所有交易或區塊已經滿了的證明,否則該區塊不會被分岔選擇規則接受
- 認證者檢查所發布的區塊體的有效性
這裡仍然有一些重要的問題需要理清楚,例如基於這種情況的主流經濟策略是出塊者提交一個空名單,這樣一來,只要誰出價最高誰就能獲勝,即使是審查創建者也能贏得競標。有一些想法可以解決這個問題和其它一些問題,但在這裡只是強調設計並不是一成不變的。
二維 KZG 方案
我們已經知道了 KZG 承諾是如何讓我們承諾數據並證明它是被正確地擴展的,然而我簡化了以太坊實際要做的事情:一個區塊將使用許多 KZG 承諾,因為無法在一個單一的 KZG 承諾中承諾所有數據。
我們已經有專用的區塊打包者,那麼為什麼不能直接讓它們創建一個巨大的 KZG 承諾呢?因為這需要一個強大的超級節點來進行重構。我們可以接受初始構建階段的超級節點需求,但我們需要避免重構時的假設。我們需要更低的資源實體處理重構,而將這些重構拆分成許多 KZG 承諾是使之可行的。重構甚至可能是相當常見的,或者說在該給定數據量的設計中,重構就是該設計中的基本情況假設。
為了使重構更容易,每個區塊將包括編碼到 m 個 KZG 承諾中的 m 個分片 blob 。雖然這樣做會導致大量的採樣,即你會在每個分片 blob 上執行數據可用性採樣,以知道它都是可用的(在 m*k 樣本中,k 是每個 blob 的樣本數)。
但以太坊將使用二維 KZG 方案,即再次使用 Reed-Solomon 編碼將 m 個承諾擴展到 2m 個承諾:

我們通過在和 0-255 同樣的多項式之上再添加額外的 KZG 承諾(這裡是 256-511)來使其成為一個二維方案。現在我們只需在上面的表格上中執行數據可用性抽樣,以確保所有跨分片數據可用。
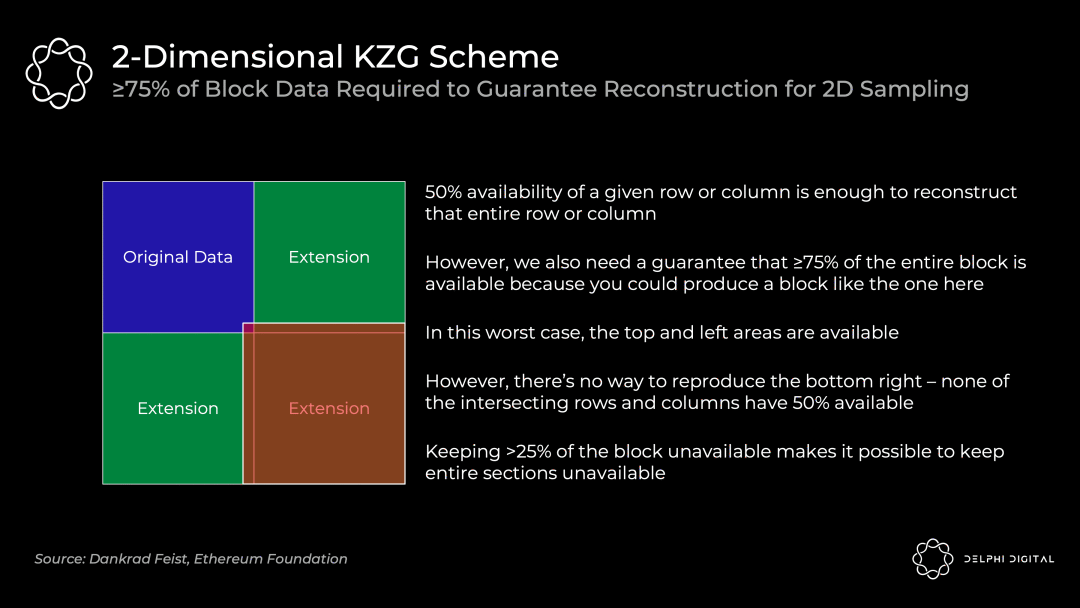
二維抽樣要求≥75% 的數據是可用的(不是之前的 50%),這意味著需要更多的固定抽樣。在前文中有提到,在一個簡單的一維方案中需要 30 個數據可用性抽樣的樣本,但在二維方案中將需要 75 個樣本才能確保重構一個可用區塊的概率相同。
分片 1.0(有一個一維 KZG 承諾方案)只需要 30 個樣本,但如果你想檢查所有 1920 個樣本的全部數據可用性,你需要對 64 個分片進行採樣,每個樣本是 512 B,所以這就需要。
(512 B x 64 個分片 x 30 個樣本) / 16 秒= 60 KB/s 帶寬
在現實中,驗證者是被輪換的,不會逐一檢查所有的分片。現在,與二維 KZG 承諾方案相結合的區塊使檢查全部數據可用性變得輕而易舉,只需要一個統一區塊的 75 個採樣樣本:
(512 B x 1 個區塊 x 75 個樣本) / 16 秒= 2.5 KB/s 寬帶
(因本文篇幅過長,後續詳見中、下篇)
免責聲明:作為區塊鏈信息平台,本站所發布文章僅代表作者及嘉賓個人觀點,與 Web3Caff 立場無關。本文內容僅用於信息分享,均不構成任何投資建議及要約,並請您遵守所在國家或地區的相關法律法規。