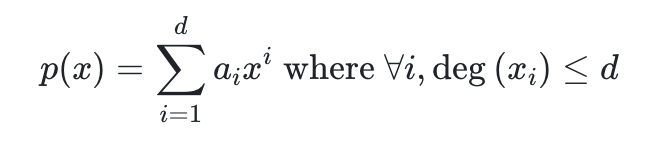在這篇文章中，我們描述了一些核心的數學和密碼學工具，以幫助你了解和評估密碼學證明系統。
原文：A Primer on Cryptographic Proof Systems (Jump Crypto)
作者： RAHUL MAGANTI, ANIRUDH SURESH
編譯： zCloak Network
原用標題（譯後）：密碼學證明系統入門
封面： Photo by Batyrkhan Shalgimbekov on Unsplash
引言
本入門文章旨在解釋可驗證計算領域的一些重要想法，特別是與構建密碼學證明系統（CPS：cryptographic proof systems）有關的一些關鍵工具。這些加密證明系統的一個關鍵優勢是，它們允許沒有大量資源的設備或實體來驗證或"檢查"一些擁有更多資源的大型實體的行為是否正確。
文中，我們首先介紹了一些數學工具，然後擴展解釋了一些核心的密碼學原語。我們希望這篇文章將會幫助到那些希望了解最近有關證明系統宣傳的人，特別是對那些希望了解使用零知識證明系統增強區塊鏈的隱私和可擴展性的人。
問題
我們有一些被稱為證明者（Prover）的實體和另一些被稱為驗證者（Verifier）的實體。證明者想向驗證者證明他知道某些計算的結果，驗證者需要有效地檢查證明者的聲明。我們稍後會更具體地定義"有效"的含義，現在讓我們把注意力集中在證明者和驗證者之間的交互概念上。這種結構可以是非常強大的！你可以讓位於 Chicago 地區的 iPhone 驗證 Los Alamos 地區的某台超級計算機的執行。
證明者發送一個信息，而驗證者回應以一個與證明者信息相應的答案。證明者再用根據他自己的上一個信息和驗證者反饋的信息來做出回應（信息），如此反复，直到驗證者接受或拒絕。
一些數學工具
這些是有關我們討論的證明系統的一些重要數學工具。
- 實數/複數：
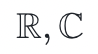
- p 階的有限域
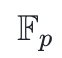，其中 p 是素數 - 群
- 我們用 (*) 表示群操作符（可以是標準的加法，乘法，或任何其他滿足下面討論的結合性、單位元和逆元三個條件的運算）。
群
群在密碼學中起著重要的作用，它可以使信息不被竊聽者察覺。
群是一個具有二元運算*、單位元和逆映射的集合。其中逆映射定義為對於這個群的所有成員，存在該群的另一個元素，使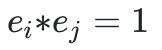
。群還必須滿足結合律：
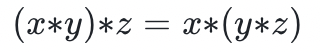
群的類型
- 交換群（Abelian group） 確保我們是否有兩個群元素 i 和 j ,
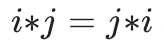
- 循環群（Cyclic group) 是一種特殊的交換群，其群元素可以由單個群元素生成（我們稱它為群生成元 g )。這意味著，如果我們從一個群元素 g 開始，並通過群操作符
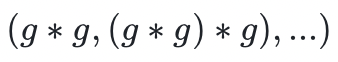對其重複應用 g ，那麼我們就可以抽取到群中的每一個元素。
在密碼學中，群實際上只是用來運行計算的對象。群之所以特別有用是因為：（1）它們可以幫助預測內存使用；（2）允許你抽取隨機數（你會發現從實數中抽取一個隨機元素非常困難——由於它是無限大的，所以抽取到任何實數的概率都是 0）。
群的力量：Diffie-Hellman 密鑰交換
群是強大的數學對象，讓我們看看群在密碼學中的一個重要用例。Diffie-Hellman 密鑰交換允許兩方，例如 Alice 和 Bob，彼此交換一些秘密 s，而不被對手竊聽而獲得這個秘密。
- Alice 和 Bob 公開商定一個生成元 g 和群
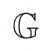
- Alice 隨機挑選一個私有數字 a ，計算出
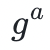並發送給 Bob - Bob 隨機選取一個私有數字 b ，計算出
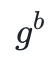並發送給 Alice - Alice 計算
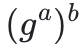
- Bob 計算
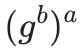
譯者註：原文寫作如此，但似應為
請注意，根據乘方規則，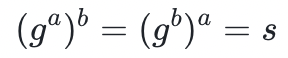
，即 Alice 和 Bob 都能計算出一個共享的秘密！現在假設一些對手 A 試圖在沒有獲得 a 或 b 的情況下也計算出秘密 s ，他們能做到嗎？讓我們通過一個簡單的群例子
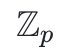來回答這個問題，在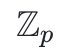中，整數模數 p 是一些非常大的素數。A 想要計算出
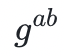，他必須找到一個
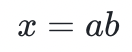，以便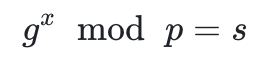
。這就是所謂的離散對數問題（Discrete-Logarithm Problem）。
對於較大的素數 p，要找到 x 這樣的解在計算上是不可行的。這是一個被普遍認可的難題，自希臘博學家 Eratosthenes（見 Eratosthenes 篩法）以來，素數因式分解就一直是一個困難的問題。事實上，2000 年來沒有人破解過這個系統！離散對數的難解性是現代密碼學的核心基礎，包括應用於像 RSA 這樣的公鑰密碼系統的發展。
譯者註：原文如此，但 RSA 公鑰密碼體系的安全性應是與大整數分解有關，和離散對數問題相關的公鑰密碼體制應為 ElGamal 加密方案。
這個例子引出了密碼系統中另一個常用的想法：計算 Diffie-Hellman 假設，即在給定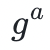和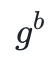的情況下，對手要計算
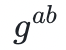在計算上是不可行的。實際上，除非某人同時知道 a 和 b，否則幾乎不可能知道秘密。
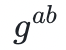橢圓曲線 (ECs：Elliptic curves)是現代密碼學的核心部分，它們並不是一個新概念，從比特幣開始它們就在區塊鏈中廣泛使用。橢圓曲線只是一種特殊類型的滿足 Diffie-Hellman 假設的群。
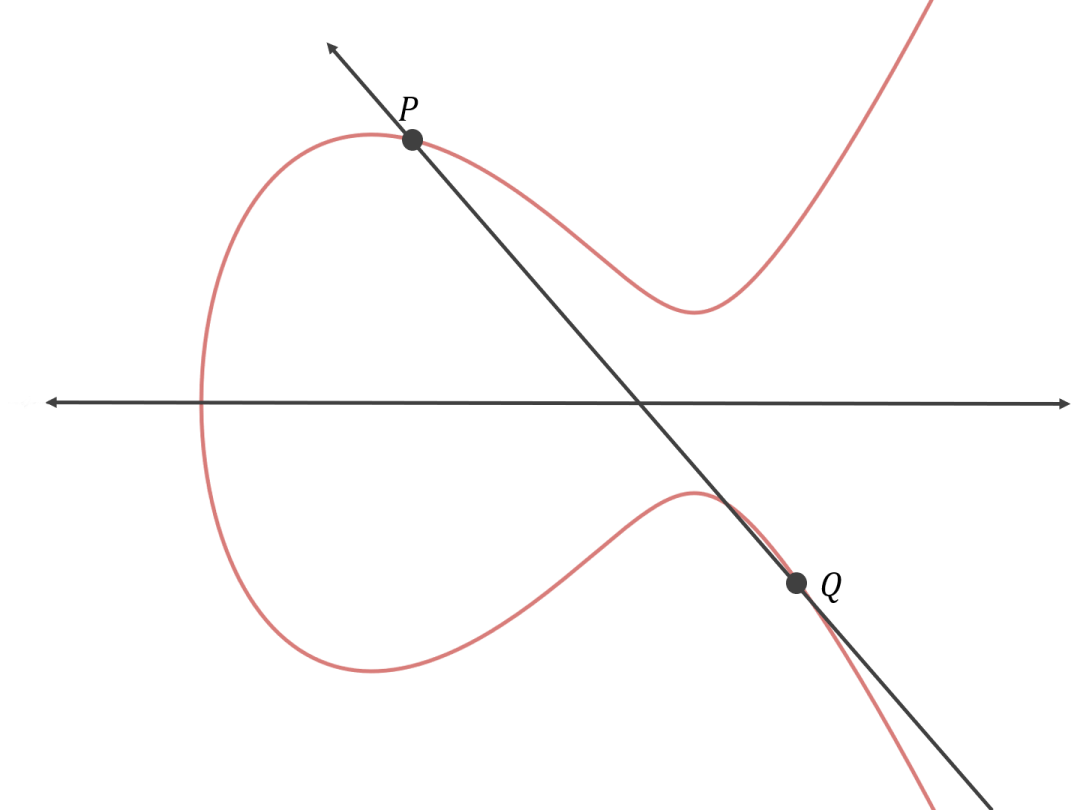
橢圓曲線背後的理論涉及很多數學，我們可以用文字總結一下橢圓曲線背後的直覺。一個橢圓曲線是一個點的集合，這些點通過以下操作構成一個群：如上圖所示，在橢圓曲線上給定兩個不同的點 P 和 Q ，連接這兩個點的線正好與橢圓曲線相交於另一個點 R ；我們將 R 穿過將曲線分成兩半的軸，得到一個也在曲線上的點 S ，我們定義
。
一個橢圓曲線密碼系統是通過選擇一個大小為 m（素數）的有限域、一個曲線方程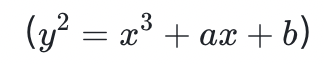
和曲線上的一個公共點 P 來定義的。私鑰是一個 t < m 的數字，而公鑰是通過* 運算符將 p 應用於自身 t 次，即通過
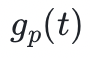將 p 應用於自身 t 次。在只知道某人公鑰的情況下，要計算他的私鑰 t 會非常困難，因為：
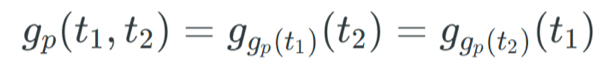
因此，分別擁有私鑰 t 1 和 t 2 的兩方 Alice 和 Bob 有可能共享一個秘密，而其他人在不知道 t 1 和 t 2 的情況下是無法計算出這個秘密的。這完全滿足了 Diffie-Hellman 密鑰交換的條件。
這意味著什麼？——我們可以使用相對較小的密鑰來實現與 RSA 等其它密碼系統類似的安全保證。
素域
域可以是實數、有理數或複數。有限域是一個僅包含有限數量元素的集合，我們為其定義了加、減、除和乘等運算，但如何實現這一點呢？如果你把一個域中的元素相加或相乘若干次，你應該得到一個此域中的數字。舉一個具體的例子：假設 1 是域
的一個元素，我們可以將 1 與其自己相加 n 次（n 是素數）。我們如何保證這個計算結果返回的元素仍然屬於這個域的成員元素？一種方法是簡單地在計算的最後加入一個餘數函數
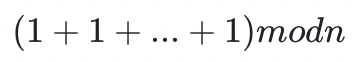
更常見的情況是，如果一個操作（加法/乘法）被應用於某個元素 e 上 m 次，其中 m > n ，你將總是得到一個屬於這個域的成員元素 e ′！更有數學經驗的讀者可能會注意到，任何域在本質上都是一個滿足某些規則的附加運算的群，但我們在這篇入門文章中不會深入探討這些細節。
多項式
多項式在密碼學和許多密碼學證明系統提供的安全保證中扮演著至關重要的角色。
定義：在某個有限域
上，總階為 d 的一元多項式 p 定義如下：
譯者註：原文如此，似應為
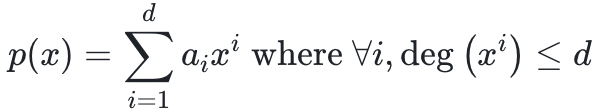
多項式在密碼學中有用的一個直觀原因是，它們能夠非常簡潔地表示大量的信息。想像以下創建一個數字表這樣具體的例子。在第一列中，你開始按順序寫下自然數（即從 1 開始的整數，這稱為求值域。現在，從第二列開始寫下實數軸上的隨機數字。如果我們在這些點上進行插值，我們就可以創建一個可以一次性表示所有這些信息的多項式！實際上，我們可以把多項式當作某個求值域上的大型真值表的連續表示。
Schwarz-Zippel引理
在這裡多項式可以派上用場。Schwarz-Zippel 引理是確保許多加密證明系統可靠性的核心工具。
定義：給出兩個不同的單變量多項式 p ，q 的階在某個有限域
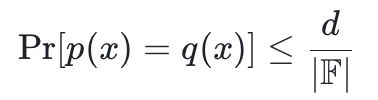
這意味著如果兩個低階多項式不相等，它們在域內的幾乎所有的點都不一致。通常加密證明系統會將一些計算（編寫是一些更高層級的抽象——比如 Solididity 代碼）轉換為多項式，然後我們可以利用這個引理來確保協議的可靠性。
一些密碼學工具
我們希望加密證明系統具有兩個主要屬性：（1）完備性；（2）可靠性。基於確定性的驗證者，完備性和可靠性定義如下:
- 完備性：給出一個驗證者總是能夠接受的真實聲明
- 可靠性：驗證者不應接受任何錯誤聲明。
現在允許驗證者拋一些硬幣（即使得驗證者非確定性）。
- 完備性：驗證者被真實聲明說服的概率（通常我們希望是 1）
- 可靠性：對於所有證明者（也包括惡意的），驗證者接受錯誤聲明的概率應該很低。
這裡的區別非常細微，但對密碼證明系統至關重要——隨機性允許我們構造可以高效運行的證明系統（通常這意味著驗證者可以在多項式時間內運行）。
Sumcheck 協議
Sumcheck 協議是交互式證明系統的基本構建模塊之一。在本質上，這個協議是定義在如下場景：一個證明者想要向一個驗證者證明它關於如下求和的知識
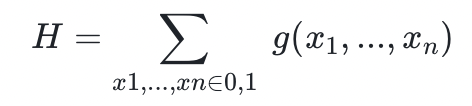
其中 g 是 n 個變量的多項式。我們假設驗證者可以預言訪問（即他們可以低成本地求值）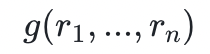
。證明者和驗證者希望相對有效地參與這一過程，而 Sumcheck 允許他們以迭代的方式進行。下面是對 Sumcheck 協議的一個直觀描述。
我們希望驗證者利用交互和隨機性，而不是對多項式求所有可能的值（指數時間問題）。通過將每個變量綁定到域中的某個隨機元素，我們可以有效地在協議的每一輪中 “剝離” 每個操作符。首先，證明者提供一個多項式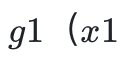
表示為：
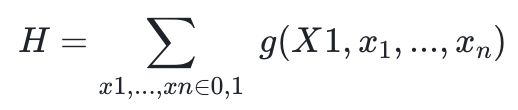
或者提供除第一個變量以外的其餘所有變量的總和（第一個變量是自由的）。我們可以看到 H 是 g 1 在 X 1 所有可能的值上的總和，事實上，驗證者檢查是否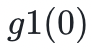
和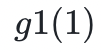
的總和確實等於 H。
如果這不是真的，那麼顯然證明者不知道這個和，但驗證者可以如此陳述。如果這是真的，驗證者不能確定證明者知道這個和——證明者可能只是幸運地挑選了一個在 X 1 所有值上的和恰好等於 H 的 g 1 ——但是證明者知道 H 的概率已經增加。
驗證者隨後對 X 1 隨機採樣一個值 r 1，然後把它發送給證明者，證明者現在的任務是發回一個表示所有變量的和（除第一個變量）的多項式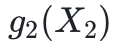
，其中，第一個變量被設為 r 1，第二個變量是固定的。我們可以看到這裡的迭代模式：驗證者將檢查從上次迭代中正確提供的 
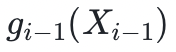是否等於本次迭代中提供的 
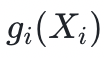對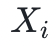
所有可能值的和。
如果在任何一點上證明者不能提供一個正確的多項式，它將被驗證者拒絕；每次它成功提供正確的下一個迭代時，它知道 H 的概率就會增加，而不只是幸運。
最後，如果證明者正確地提供了最後一次迭代（多項式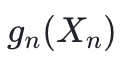
），驗證者就會得出結論：證明者俱有非常高的概率知道 H。
為什麼這很有用呢？
- 現在我們了解了
Sumcheck，讓我們把它當作一個黑箱算法，用來證明某些計算實際上是有效的。 - 使用
Sumcheck的高級方法是用布爾超立方體上的和來重寫你想設計協議裡的一些計算。通過將我們的問題還原為Sumcheck的實例，我們就可以非常輕鬆地應用它了！
GKR 協議
讓我們來看看 Sumcheck 的一個具體用例。GKR 協議是一個迷人的、聰明的協議，用於有效地驗證可被表達為低深度算術電路的計算。這是最早的嘗試之一，提出一個可以驗證一類非常普遍的計算的系統（不僅僅是布爾超立方上的和）。順便說一句，它使用了 Sumcheck 作為算法的支柱。
這裡有一個基本結構--我們有一些可以用不同層來表達的計算。直觀地說，我們可以讓驗證者只是重新運行電路的計算，並檢查驗證者的輸出是否與聲明的輸出一致。但這非常低效。相反，讓我們嘗試利用電路的結構來降低驗證者的時間複雜性。
基本的直觀判斷是這樣的：我們把對電路第 i 層的聲明還原為對第 i+1 層的聲明。我們按照這個過程進行歸納，把聲明一直還原到只是在一組隨機點上評估一個多項式，而不是評估整個電路。
算術電路到底是什麼
我們已經討論了一些數學對象，如對建立加密證明系統有用的多項式，但我們還沒有談及我們如何實際計算它們。算術電路是一種簡單明了的方式來表示評估多項式時涉及的計算。算術電路類似於計算機和電子產品中使用的邏輯電路。在電子芯片中，我們有一堆相連的門（AND，OR，NOT，XOR，等等）。我們給這些門一些輸入，並將某個門的輸出作為下個門的輸入。但是，我們用加法和乘法等算術運算取代了這些邏輯運算符。我們得到如下的東西：
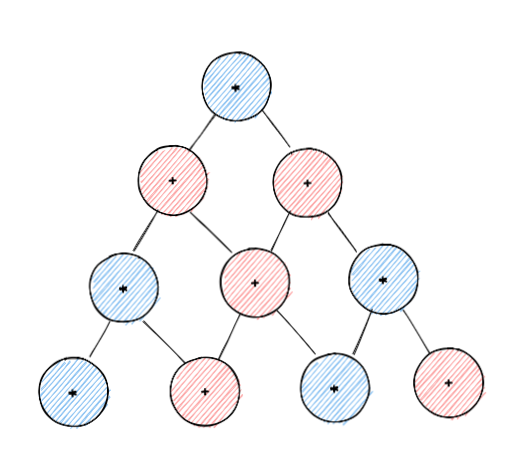
多項式承諾方案
多項式承諾方案（PCS：Polynomial Commitment Schemes）對加密證明系統的運作極為重要。在一個非常基礎的層面上，它確保證明者在與驗證者互動時不能作弊，也就是說，證明者不能根據驗證者正在抽取的隨機點來改變他之前的信息，我們把這個屬性稱為非自適性（non-adaptivity）。前文提及的 Sumcheck 協議說到，我們希望證明者在驗證者發送隨機點之前對多項式做出承諾（承諾方案是確保證明者行為誠實的一種有力方式）。我們將在後面的文章中看到，多項式承諾方案在確保加密證明系統的安全性方面起著關鍵作用。
如下是這個方案的工作原理：
- 證明者對一些參考字符串進行承諾
- 驗證者如何知道證明者確實承諾了這個多項式？
- 驗證者要求證明者在某個隨機點計算多項式
- 證明者在橢圓曲線上的某個點發回多項式的計算值
結語
在這篇文章中，我們描述了一些核心的數學和密碼學工具，以幫助你了解和評估密碼學證明系統。我們希望你能發現這篇文章既令人興奮又有助於解開一些通常很神秘的"月球數學"，這些 “月球數學” 涉及到構建你最喜歡的私有 L1、可擴展的 L2 或零知識驅動的應用程序。有了這個背景，希望你能更好地準備好去挖掘其它證明系統的一些內部工作原理。
免責聲明：作為區塊鏈信息平台，本站所發布文章僅代表作者及嘉賓個人觀點，與 Web3Caff 立場無關。本文內容僅用於信息分享，均不構成任何投資建議及要約，並請您遵守所在國家或地區的相關法律法規。
