STARK 提供了一種功能強大的方法,可用於以無信任的方式驗證在公共數據上執行的計算的正確性。
原文:Safe and Sound – A Deep Dive into STARK Security(Starknet)
封面:STARK

STARK 完整安全性的深度分析
TL; DR
- 非互動式 STARK 來源於互動式預言機證明(IOP),並在隨機預言機模型中編譯成非互動式證明。
- 這篇文章解釋了 ethSTARK 文檔的最新更新,其中對隨機預言機模型中 ethSTARK 協定的安全性進行了全面而具體的分析。
STARK 安全性詳解
STARK 證明系統(可擴展的透明知識論證)是一個強大的計算完整性工具:它允許以一種無信任的方式驗證在公共數據上執行的計算的正確性。 在這篇文章中,我們將深入探討 STARK 證明所提供的安全性,對其進行定義,並探索證明方案安全性的技術。
(詳情請閱讀 ethSTARK 文檔(1.2 版)第 6 節,以及 Block 等人就此主題所做的重要而全面的獨立工作)。
我們的安全分析要達到什麼目的? 我們希望防止對 STARK 系統的「成功攻擊」,這種攻擊是由虛假陳述和 STARK 驗證者接受的針對該(虛假)陳述的 STARK 證明引起的。 由於虛假陳述是很危險的,而且它們可能以各種規模和形式出現,因此我們希望能夠安全地防範所有虛假陳述。 任何虛假陳述,即使是微不足道的 1+1=3,只要與 STARK 驗證者接受的 STARK 證明相結合,就會被視為對系統的成功攻擊。(有密碼學背景的人可能有興趣知道,STARK 還滿足更強的安全概念,如知識可靠性,但為了簡單起見,這篇文章將重點討論更簡單的可靠性)。
我們如何正式定義 STARK 系統的安全性? 我們通過分析 “ 可靠性誤差” 來實現。 “ 卡考性誤差「大致衡量了攻擊者構建一次成功攻擊所需的預期」成本”(即為一個虛假陳述找到一個 STARK 證明,但該虛假陳述仍被 STARK 驗證者接受)。 從數學上講,可靠性誤差是一個函數 e(t),它的輸入是時間參數 “t”,代表攻擊者為發起攻擊所願意花費的計算時間,輸出則是攻擊者攻擊成功的概率(為虛假陳述找到令人信服的證明)。 隨著攻擊者願意花費的 “ 成本” t 的增加,其成功概率也會增加。
到目前為止,我們已經將 STARKs 的安全性定義為一個函數 e(t),這與你們在加密推特上討論安全性的方式不同。 在推特上,你可能會聽到這樣的說法:“ 該方案有 96 比特的安全性”。 這種說法如何轉化為我們對安全的定義? 對此沒有統一的答案,因為人們對「x 比特安全性」的理解略有不同:
嚴格解釋的話,對於在 1 和 2⁹⁶之間的任何 t,可靠性誤差為 e(t)≤ 2⁹⁶。 這意味著任何運行時間不超過 2⁹⁶的攻擊者成功的概率很小,小於 1/2⁹⁶,即小於十億分之一乘以十億分之一。
一種更寬鬆、或許也更常見的解釋是,96 比特的安全性意味著對於任意 t 都有,t/e(t)≥ 2⁹⁶的情況。 這意味著成功概率與運行時間成(反)線性關係。 例如,如果攻擊者的運行時間為 2⁸⁶,則其成功概率最多為 1/2 ¹⁰。
在本文中,我們將討論第二種方案。
從 IOP 到具有 96 比特安全性的 STARK
那麼,我們如何證明一個方案具有 96 比特的安全性呢? 要回答這個問題,我們需要瞭解 STARK 的高層結構。 STARK 由三個主要部分組成:IOP(互動式預言機證明)、默克爾樹和 Fiat-Shamir 哈希; 我們將重點討論的部分是 IOP。 一旦指定了這些元件,我們就可以將它們編譯成 STARK。 以下,我們將詳細介紹這些元件、它們是什麼以及如何將它們組合在一起。
我們要審查的第一個元件是 IOP:IOP 類似於標準的互動式證明,即證明者和驗證者進行多輪交互(我們僅限於公共幣協定,即驗證者只向證明者發送隨機挑戰)。 在 IOP 中,驗證者不會完全讀取證明者的資訊,而是從每條證明者資訊中抽取少量比特。 這就是後來編譯的 STARK 的簡潔性所在。
有了 IOP,如何從中構建 STARK? 證明者的資訊可能很長(實際上,它們比計算本身還要長)。 為了壓縮信息,我們使用默克爾樹。 默克爾樹是一棵二進位哈希樹,其中每個葉節點代表 IOP 中的一個查詢或一個答案。 樹根是整個信息的承諾。 當驗證者想要讀取資訊中的特定位置時,證明者會提供該位置的值和驗證路徑。 驗證者就可以使用該路徑來驗證該值是否正確。 IOP 驗證者只從證明者資訊中讀取少量位置資訊。 因此,使用默克爾樹可以實現簡潔的協定(通信量小)。
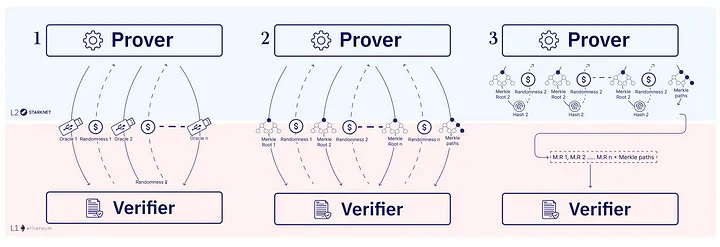
壓縮輪次
我們可以選擇互動式 STARK,但為了簡化生成 STARK 的過程,我們通常會選擇非互動式 STARK,這樣驗證者在構建 STARK 時就無需等待外部資訊。 事實上,這是目前所有 STARK 系統的部署方式,也是 ethSTARK 協定的構造方式。 非互動式 STARK 也是透明 SNARK 的一種特例(透明意味著無需可信設置即可實例化; 這也被稱為「Arthur Merlin 協定」或「公共硬幣 IOP」)。 為此,最後一步是應用 Fiat-Shamir 演算法將各輪壓縮為一條資訊,我們稱之為 STARK 證明。 Fiat-Shamir 轉換是將互動式協議轉換為非互動式協定的方法。 驗證者在 “ 與哈希函數對話「時模擬互動式協定」。 為了得出第 i 輪的隨機挑戰,驗證者對第 i 輪之前的部分副本進行散列,並將輸出解釋為下一個挑戰。
這就確保了驗證者在挑戰生成后無法更改自己的回答。 然而,作弊驗證者有了一些新的策略途徑,這是互動式 IOP 所沒有的。 驗證者可以通過修改最後一條驗證者資訊來重新生成驗證者的挑戰,這樣就會有新的記錄,從而產生新的挑戰。 事實證明,IOP 的標準可靠性概念不足以證明 Fiat-Shamir 轉換的安全性。
例如,一個有 96 輪的 IOP,並向驗證者添加如下 “hack”:如果驗證者隨機性的第一比特在 96 輪中每一輪都是 0,那麼驗證者就會接受(無需查看任何證明)。 我們可以看到,在驗證者中加入這一 hack 技術只會給 IOP 的可靠性誤差增加 1/2⁹⁶ 的項。 然而,經過 Fiat-Shamir 轉換後,攻擊者可以輕鬆修改驗證者資訊,確保每個哈希值都以 0 開頭,從而在很短的時間內破解系統。 請放心,這種可怕的情況只是一個理論上的例子,並不適用於已部署的 STARK。 那麼,讓我們來看看為什麼我們的 STARKs 始終是安全的? 簡而言之,我們將證明攻擊者最多運行 t 步,攻擊成功的概率為 e(t)≤ t / 2⁹⁶。 詳情如下。
IOP 和逐輪可靠性
STARK 的安全性取決於其底層 IOP。 但是,一個 IOP 具有 96 比特的安全性意味著什麼呢? 按照標準定義,IOP 的可靠性誤差為 1/2⁹⁶:這意味著任何攻擊者(無論運行時間長短)騙過驗證者的概率最多為 1/2⁹⁶。 然而,正如我們所討論的,IOP 可靠性只是三個部分中的一個,這不足以讓從所有三個步驟中編譯出來的 STARK 獲得 96 比特的安全性。 取而代之的是,假設 STARK 有 96 比特逐輪可靠性誤差(有時也使用一個被稱為狀態恢復可靠性的類似定義),那麼編譯后的 STARK 的安全性就得到了證明。
直觀地說,逐輪可靠性是指每一輪都有 96 比特的安全性,而不僅僅是整個協定。 更詳細地說,逐輪可靠性是指存在一個謂詞,它能獲取協定的部分記錄,並告訴我們這個記錄是否是 “ 欺騙性的”: “空記錄” 不是 “ 欺騙性的”,而完整記錄則是 “ 欺騙性的”,當且僅當驗證者接受它時。 最後,對於任何不是 “ 欺騙「驗證者的部分文字記錄,在下一輪中該文字記錄變成」欺騙性的” 的概率最多為 1/2⁹⁶。 如果存在這樣一個具有這些特性的謂詞,我們就說該協定具有 96 比特逐輪可靠性(該謂詞不要求可有效計算)。
在許多情況下,只分析 IOP 的可靠性,而不分析其逐輪可靠性。 誠然,我們很難想到 IOP 具有標準可靠性而不具有逐輪可靠性的例子(人為製造的例子除外)。 不過,在推導具體的安全邊界時,兩者之間的差異可能會出現,因為每個比特都很重要。 因此,要推導出嚴密而具體的邊界,就必須對 IOP 的逐輪可靠性進行嚴密分析。 這正是我們對 FRI 協議和作為 STARKs IOP 基礎的 ethSTARK IOP 所做的工作。 分析本身遠非小事,也超出了本篇文章的範圍。 利用新的分析方法,我們可以為我們的證明設置精確的參數。
逐輪可靠性確實為我們提供了所需的保證。 證明者可以多次重新生成挑戰,但我們知道,在任何一輪中,生成 “ 欺騙性” 記錄的概率都是 1/2⁹⁶。 因此,如果驗證者的時間為 t(以哈希調用次數來衡量),那麼它最多可以嘗試 t 次來獲得「欺騙性的」文字,這就將其成功概率限制
e(t) ≤ min*{t /2⁹⁶,1}* 。
添加所有錯誤項
最後,要使所有這一切成立,我們需要確保驗證者無法篡改默克爾樹。 我們可以證明,只要證明者在哈希函數中沒有發現碰撞,它就無法在默克爾樹中作弊。 攻擊者使用 t 次調用(隨機哈希函數)找到碰撞的概率至多為 min{t²/2s,1},其中 s 是哈希函數的輸出長度(這是 “ 生日悖論” 造成的)。 這就是為什麼我們要設置哈希函數的長度為所需安全性的兩倍。 因此,如果我們有一個輸出長度為 192 比特的哈希函數和一個逐輪可靠性為 96 比特的 IOP,我們就能得到一個編譯後的 STARK,其穩健性誤差為 e(t)= t /2⁹⁶ + min*{t² / 2¹⁹²,1}.。 特別是,由於我們用來定義安全性的函數 t/e(t)滿足不等式 t/e(t)≥ t/(t /2⁹⁶ + min{t² / 2¹⁹²,1}),* 而這個不等式的右邊在 t=2⁹⁶ 時達到最小值,對於這個 t 值,我們有 t/e(t)≥ 2⁹⁵,因此這種方案擁有 95 比特的安全性。
總結
總之,STARK 提供了一種功能強大的方法,可用於以無信任的方式驗證在公共數據上執行的計算的正確性。 STARK 的安全性通常用「可靠性誤差」來衡量,它表示攻擊者成功提供虛假陳述並用證明說服驗證者的概率。 要達到理想的安全等級(如 96 比特),底層 IOP 必須滿足逐輪可靠性,確保每一輪都能保持較高的安全等級。 我們分析了 SATRK 所依據的 IOP 的逐輪可靠性,從而得出了具體的安全界限。
免責聲明:作為區塊鏈資訊平臺,本站所發佈文章僅代表作者及嘉賓個人觀點,與 Web3Caff 立場無關。 文章內的資訊僅供參考,均不構成任何投資建議及要約,並請您遵守所在國家或地區的相關法律法規。













