本文主要研究橢圓曲線加密演算法中的扭曲曲線攻擊。
作者: Johan,慢霧安全團隊
據慢霧安全團隊情報,2023 年 3 月 13 日,Ethereum 鏈上的借貸專案 Euler Finance 遭到攻擊,攻擊者獲利約 2 億美元。
駭客在攻擊完 Euler 後,為了混淆視聽逃避追查,轉了 100 ETH 給盜取了 Ronin 6.25 億多美金的駭客拉撒路。 拉撒路順水推舟將計就計,隨即給 Euler 駭客發了一條鏈上加密消息 [1],並回禮了 2 枚 ETH:

消息內容是提示 Euler Exploiter 用 eth-ecies[2] 解密這條消息。
質疑
按道理說在公開的環境下,如果 Ronin Exploiter 只是想加密通訊,使用公鑰加密是最簡單的方案。
公鑰加密:
C = {rG, M + rQ} = {C1, C2}
私密金鑰解金:
M = M + r(dG) − d(rG) = C2 − d(C1)
其中密文 C,公鑰 Q,私鑰 d,隨機數 r,消息 M。 協議很簡單,加密過程不需要用到的私鑰,不存在私鑰洩露的路徑。
使用 eth-ecies 加密是因為方便還是另有所圖? 隨後很快就有人指出 eth-ecies 存在安全漏洞,Ronin Exploiter 是想竊取 Euler Exploiter 的私鑰。
是否真的如此? 且讓我們先分析一下 eth-ecies 存在的是怎麼樣的一個漏洞。
扭曲攻擊漏洞
經過分析,我們發現 eth-ecies 使用了 “elliptic”: “^6.4.0”,這是個 Javascript 橢圓曲線庫,這個版本的庫存在多個安全漏洞,其中一個就是扭曲曲線攻擊漏洞(twist attacks),這個漏洞的成因是在計算 ECDH 共用密鑰時沒有驗證對方的公鑰是否在曲線上,攻擊者可通過構造小子群曲線上的公鑰, 誘導受害者計算共用金鑰,從而破解出受害者私鑰。

但是这个漏洞的利用难度是很高的,需要有非常契合的场景才能发起攻击,Ronin Exploiter 是否有机会发起扭曲攻击呢?
ECDH 算法风险
ECDH 算法是基于椭圆曲线加密的密钥交换算法。它与传统的 Diffie-Hellman (DH) 算法类似,但是使⽤的是椭圆曲线上的数学运算来实现密钥交换,从⽽提供更⾼的安全性。
下⾯是 ECDH 算法的步骤:
- ⽣成椭圆曲线:在密钥交换之前,通信双⽅需要选择⼀个椭圆曲线,该曲线必须满足⼀些数学特性,例如离散对数问题。
- ⽣成私钥和公钥:每个通信⽅都需要⽣成⼀对私钥和公钥。私钥是⼀个随机数,用于计算公钥。公钥是⼀个点,它在椭圆曲线上,并由私钥计算得出。
- 交换公钥:通信双方将自己的公钥发送给对方。
- 计算共享密钥:通信双方使用对方发送的公钥和自己的私钥计算出⼀个共享密钥。这个共享密钥可以⽤于加密通信中的数据,保证通信的机密性。
为了⽅便描述下⽂ Alice 和 Bob 分别代表上⾯双方,G 为基点,假设:
Alice 的私钥是 a,则 Alice 公钥是 A = aG;
Bob 的私钥中 b,则 Bob 公钥是 B = bG。
核⼼知识点在共享密钥计算⽅法,根据群的乘法交换律,他们只要获取到对⽅的公钥就可以计算出共享密钥:
S = aB = a(bG) = b(aG) = bA
如果 Alice 想要刺探 Bob 的私钥,她可以选择⼀个阶数 q ⾮常⼩(点的数量⾮常少)的曲线点 H(这个点不是对应任何特定私钥的公钥,但是 Bob 并不知道),由于群是循环群,Bob 在计算 S′ = bH 时,他得到的 S′ 将在这些少量点群以内。Alice 不知道 Bob 的私钥 b,但可以通过穷举得到满⾜ S′ = xH 的 x,此时 b ≡ x mod q 。显然 x 很⼩,最⼤为 q。
仅知道⼀个模余是不够的,要知道私钥是⼀个很⼤的数,最⼤可以达到 图片,⼀个模余在这个范围可以推出⾮常多的解,所以需要给 Bob 多个这类扭曲的点 H 让 Bob 计算,这样就可以就可以通过计算推出唯⼀解。
需要多少个扭曲点呢?这取决于每⼀次选择的阶数 q,需要阶数相乘能超过私钥的最⼤值,即满⾜:

如果我每次选择的 q ⼤⼀点,那么需要交互的次数 n 就可以少⼀点,但 q 越⼤意味着穷举的难度越⼤,所以这⾥需要根据 Alice 的运算性能做⼀个取舍。
事件结论
上⾯我们分析了 ECDH 算法的⻛险和攻击原理,我们再回来看 eth-ecies 这个库,实际上它使用的只是⼀个类似 ECDH 的算法,它在构造共享私钥时使⽤的是临时密钥,根本不需要用到加密方的私钥,所以并不会对加密方构成风险。
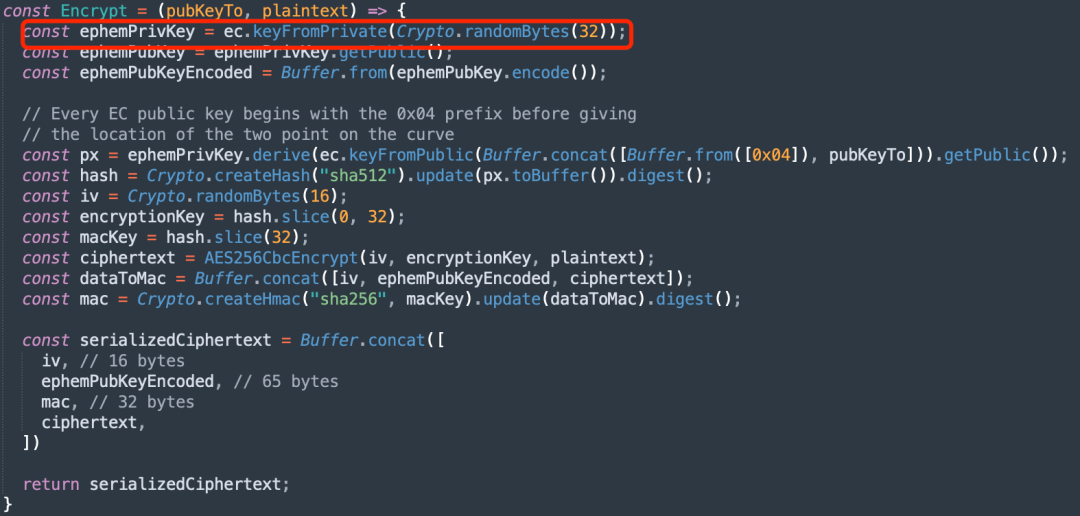
那么有没有可能 Ronin Exploiter 是想利⽤社会⼯程学引导 Euler Exploiter 使⽤其它有问题的⼯具呢?⽐如我们熟知的 PGP 加密协议?
巧的很,我们很快就发现被⼴泛使⽤的开源库 openpgpjs[3] 最新版本 v5.7.0 还在使⽤了低版本的 “@openpgp/elliptic”: “^6.5.1” ,更巧的是,它⽀持基于 Curve25519 的 ECDH 协议,故事本应该进⼊⾼潮,但经过分析发现,openpgpjs 的 ECDH 协议在实现时,和 Ecies 协议⼀样引⼊了临时密钥,即使加密⽅导⼊了私钥,也仅仅⽤于消息签名,⽽不会⽤于构造共享密钥。

故事结束了,我觉得 Ronin Exploiter 使⽤低版本 elliptic 存在的漏洞去隐秘的窃取 Euler Exploiter 私钥的可能性不⼤,⾄于那条链上消息,可能真的是为了共商⼤计,更进⼀步的图谋不轨需要更加⾼超的社会⼯程学⼿段了,但 Euler Exploiter 已经警觉。
意犹未尽
上面提到了扭曲攻击的原理,实际⼯程实现上仍然有⼏个问题需要解决:
- 如何构造扭曲的点?
- 当 Bob ⽤共享密钥 S’ 加密消息时,它并不会把 S’ 传输给 Alice,因为根据协议 Bob 认为 Alice 是已经知道这个密钥的,那么 Alice 如何获取 S’ 呢?
- ⼤恶魔 Alice 最终获取到⼀系列共享密钥 图片,她可以⽤什么⽅法恢复出 Bob 的私钥?
这⾥以 Curve25519 曲线为例,它的曲线方程是:

我们随意改变其中的⼀个参数,得到⼀条新的曲线,比如:

使⽤ sagemath 数学软件来表示 [4]:
p = 2**255-19
E = EllipticCurve(GF(p), [0,48666,0,1,0])然后我们计算它的阶数,并对这个阶数进⾏因式分解:
Grp = E.abelian_group()
G = Grp.gens()[0]
Gorder = G.order()
print( "{0} = {1}".format(Gorder, factor(Gorder)) )计算结果:
...= 2 * 3049 * 14821 * 19442993 * 32947377140686418620740736789682514948650410565397852612808537选择 19442993 这个⼤⼩适中的数,⽤中国剩余定理创建⼀个含有 19442993 个元素的⼦群:
x = crt([1,0], [19442993, Gorder//19442993])
P1 = x * G
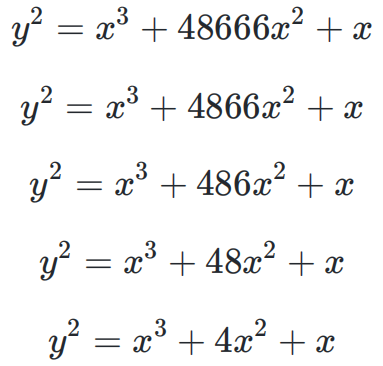
最终得到的结果可表示为:

使⽤中国剩余定理即可计算出私钥 b:
x = crt([ x1, x2, x3, x4, x5, x6, x7, x8, x9], [ 19442993, 3645143, 184879577, 5110460161, 15272631587, 208137522259, 64927105657, 60824497, 213156431])
print(x == b)
print(hex(x))總結
本文我們通過一個不同常理的對話開始研究了橢圓曲線加密演算法中的扭曲曲線攻擊,分析了漏洞的存在的原因,雖然漏洞利用場景有限,但不失為一個很有價值的漏洞,希望能對大家的學習研究有所啟發。
最後,感謝領先的一站式數字資產自託管服務商 Safeheron 提供的專業技術建議。
參考資料:[1].https://etherscan.io/tx/0xcf0b3487dc443f1ef92b4fe27ff7f89e07588cdc0e2b37d50adb8158c697cea6
[2]. https://github.com/LimelabsTech/eth-ecies
[3]. GitHub – openpgpjs/openpgpjs: OpenPGP implementation for JavaScript
[4]. Elliptic curve constructor – Elliptic curves
免責聲明:作為區塊鏈資訊平臺,本站所發佈文章僅代表作者及嘉賓個人觀點,與 Web3Caff 立場無關。 文章內的資訊僅供參考,均不構成任何投資建議及要約,並請您遵守所在國家或地區的相關法律法規。













