Safeheron 深層剖析 Ed25519 私鑰提取攻擊的來龍去脈。
作者: Max @ Safeheron Team
最近大家開始討論 Ed25519 簽名算法庫的安全問題。一言蔽之,由於一些算法庫設計上的不周,以及用戶對算法庫接口的錯誤使用,可能導致這樣的風險:攻擊者通過分析同一消息的兩次不同簽名結果,提取出用戶私鑰。
為了向大家解釋一下這個問題的來龍去脈。本文會按照如下篇章來深入和全面的介紹:
- 為什麼使用 Ed25519 簽名?
- 一圖掌握 Ed25519 簽名原理
- Ed25519 簽名的數學表述
- 算法工程實現與私鑰提取攻擊
- 攻擊影響範圍和解決辦法
- 關於攻擊的進一步思考
為什麼使用 Ed25519 簽名?
Ed25519 是美籍德裔密碼學家 Daniel J. Bernstein 等人基於 25519 系列橢圓曲線所設計的橢圓曲線簽名算法。其中,25519 系列橢圓曲線也是由 Daniel J. Bernstein 本人首次在 2005 年獨立提出的。Ed25519 算法具有以下優勢:
更開放的設計
相比 NIST 系列標準中的橢圓曲線而言,25519 系列橢圓曲線的各參數的選擇完全開放透明,無任何可疑之處;
更高的安全性
25519 系列橢圓曲線經過特別設計,將出錯的概率降到了最低,從實踐上來說更加安全。比如,任何一個 32 位隨機數都是一個合法的 X25519 公鑰,從而避免了惡意數值攻擊的可能;
更快的計算速度
25519 系列曲線是目前計算速度最快的橢圓曲線。因為這些原因,越來越多的區塊鏈採用了 Ed25519 作為其簽名算法。
一圖掌握 Ed25519 的簽名原理

如上所示,一張圖就描述清楚了 Ed25519 的原理,幾乎囊括了所有的算法細節。如果讀者需要了解 Ed25519 算法,讀懂上面這張圖即可。這裡我們不會糾結於算法的所有細節。從感官上來說,Ed25519 簽名算法的設計看起來要比更加常見的 ECDSA 簽名算法要復雜一些,兩者之間差異巨大。
Ed25519 簽名的數學表述
我們會順帶介紹另一種跟 Ed25519 有親戚關係的算法。讀者如果比較了解 Schnorr 簽名算法,就會在 Ed25519 簽名算法中發現一種熟悉感。Ed25519 算法其實是 Schnorr 算法的一種變型,主要差別有兩個:
- 前者多次使用了確定性隨機數,甚至為此調整了私鑰設計;
- 前者將橢圓曲線從常見的 Short 橢圓曲線 Secp256k1/Secp256r1 等更換成扭曲愛德華橢圓曲線 Ed25519。
讓我們回歸到 Schnorr 算法的架構下,描述一下 Ed25519 的數學邏輯。通過概括上圖,Ed25519 簽名算法可以定義為:

算法工程實現與私鑰提取攻擊
Ed25519 簽名的變型實現
現實當中,很多算法庫在實現 Ed25519 簽名算法時,並不會嚴格按照上圖來實現。出於效率和使用方便考慮,公鑰 通常不會重新計算,它會被暫存起來。在簽名的時候,公鑰 作為已有值,直接參與簽名計算,如下所示。

錢包架構
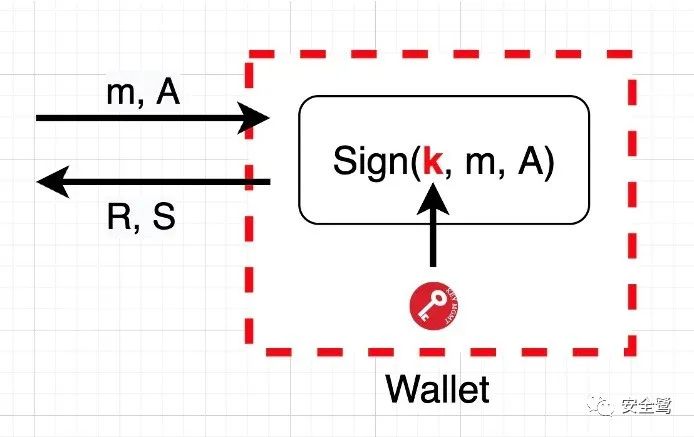
如上圖所示,描述一種通用的錢包架構,包括移動端錢包、硬件錢包、雲錢包(運行在雲端服務器上)等多種場景。在錢包架構中,私鑰通常被保存在安全的場合,無法被外界直接訪問,但可以參與簽名計算。
私鑰提取攻擊
如何發起攻擊呢?只要發起兩次簽名,每次簽名時使用不同公鑰(比如分別使用 和)即可。

需要強調的是,我們不需要完全提取出私鑰 , 只要能提取出 ,就能對任意消息進行簽名。因此,從數字資產安全的角度來說,只要能提取出 , 就等同於錢包私鑰被徹底獲取了,獲取了私鑰即獲取了資產。
攻擊影響範圍和解決辦法
不管是哪種錢包,移動端錢包、雲錢包、硬件錢包,只要是按照這種方式設計 Ed25519 簽名算法,即提供形如 的接口,且沒有對公鑰 進行驗證,就可能遭受這種攻擊。
補充一句,這種攻擊方法對 Schnorr 依然有效。
解決辦法也很簡單,分兩種處理辦法:
- 不要提供形如 的接口,只提供形如 的接口。通過私鑰 來計算 ,避免非法輸入;
- 如果必須提供形如 的接口,一定要驗證 ,即保證輸入公鑰是合法且唯一的。
儘管這個攻擊方式是切實有效的,大家也不需要過分擔憂它帶來的威脅。大多數實際場景中, 接口的調用方就是用戶自己,而不是第三方(潛在的攻擊方),輸入公鑰 也是合法的,因此不用擔心遭受私鑰提取攻擊。如果 接口的調用方為第三方,就需要謹慎預防此類攻擊。
關於攻擊的進一步思考
這種攻擊背後的思想到底是什麼呢?大家可以發現,Ed25519 和 Schnorr 算法中多次使用了確定性隨機數(Deterministic Random Number),這也許能解釋背後攻擊的根源。並不是說使用確定性隨機數就是錯的。恰恰相反,當一個簽名系統的各個參數都是確定性的時候,系統可以是安全的,甚至相對於隨機簽名系統而言,具有某些更加安全的特性,比如針對相同的消息始終產生相同的簽名。但是,當一部分確定性被打破(通常是由於工程實現和使用的考慮不周)的時候,噩夢就開始了。剩餘的確定性非但不能保證安全,反而可以被攻擊者利用起來,通過重複簽名,消去確定性不變量,實現對整個系統的攻擊。對 Ed25519 簽名算法和 Schnorr 簽名算法的攻擊,就能部分佐證這種思想。
從以上思想出發,預防這種攻擊還有一種全新的方案,那就是,用 “真” 隨機數完全取代確定性隨機數,通過消除確定性來避免此種依賴於重複簽名的私鑰提取攻擊。這種方法的具體應用,限於篇幅,以後有機會我給大家介紹。
參考文獻
[1] High-speed high-security signatures . Daniel J. Bernstein. [2] Edwards-Curve Digital Signature Algorithm (EdDSA) Josefsson, S. [3] ed25519-unsafe-libs免責聲明:作為區塊鏈信息平台,本站所發布文章僅代表作者及嘉賓個人觀點,與 Web3Caff 立場無關。本文內容僅用於信息分享,均不構成任何投資建議及要約,並請您遵守所在國家或地區的相關法律法規。













