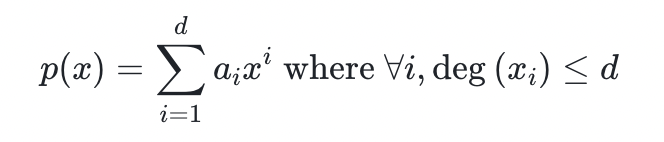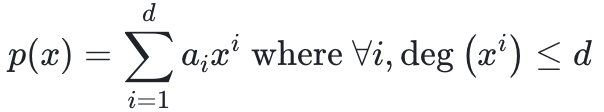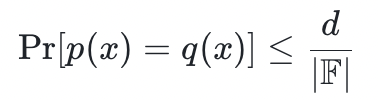在这篇文章中,我们描述了一些核心的数学和密码学工具,以帮助你了解和评估密码学证明系统。
原文:A Primer on Cryptographic Proof Systems (Jump Crypto)
作者:RAHUL MAGANTI, ANIRUDH SURESH
编译:zCloak Network
原用标题(译后):密码学证明系统入门
封面:Photo by Batyrkhan Shalgimbekov on Unsplash
引言
本入门文章旨在解释可验证计算领域的一些重要想法,特别是与构建密码学证明系统(CPS:cryptographic proof systems)有关的一些关键工具。这些加密证明系统的一个关键优势是,它们允许没有大量资源的设备或实体来验证或 "检查 "一些拥有更多资源的大型实体的行为是否正确。
文中,我们首先介绍了一些数学工具,然后扩展解释了一些核心的密码学原语。我们希望这篇文章将会帮助到那些希望了解最近有关证明系统宣传的人,特别是对那些希望了解使用零知识证明系统增强区块链的隐私和可扩展性的人。
问题
我们有一些被称为证明者(Prover)的实体和另一些被称为验证者(Verifier)的实体。证明者想向验证者证明他知道某些计算的结果,验证者需要有效地检查证明者的声明。我们稍后会更具体地定义 "有效 "的含义,现在让我们把注意力集中在证明者和验证者之间的交互概念上。这种结构可以是非常强大的!你可以让位于 Chicago 地区的 iPhone 验证 Los Alamos 地区的某台超级计算机的执行。
证明者发送一个信息,而验证者回应以一个与证明者信息相应的答案。证明者再用根据他自己的上一个信息和验证者反馈的信息来做出回应(信息),如此反复,直到验证者接受或拒绝。

一些数学工具
这些是有关我们讨论的证明系统的一些重要数学工具。
- 实数/复数:

- p 阶的有限域
 ,其中 p 是素数
,其中 p 是素数 - 群

- 我们用 (*) 表示群操作符(可以是标准的加法,乘法,或任何其他满足下面讨论的结合性、单位元和逆元三个条件的运算)。
群
群在密码学中起着重要的作用,它可以使信息不被窃听者察觉。
群是一个具有二元运算 *、单位元和逆映射的集合。其中逆映射定义为对于这个群的所有成员,存在该群的另一个元素,使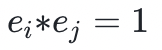 。群还必须满足结合律:
。群还必须满足结合律:
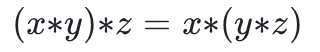
群的类型
- 交换群(Abelian group) 确保我们是否有两个群元素 i 和 j ,

- 循环群(Cyclic group) 是一种特殊的交换群,其群元素可以由单个群元素生成(我们称它为群生成元 g )。这意味着,如果我们从一个群元素 g 开始,并通过群操作符
 对其重复应用 g ,那么我们就可以抽取到群中的每一个元素。
对其重复应用 g ,那么我们就可以抽取到群中的每一个元素。
在密码学中,群实际上只是用来运行计算的对象。群之所以特别有用是因为:(1)它们可以帮助预测内存使用;(2)允许你抽取随机数(你会发现从实数中抽取一个随机元素非常困难——由于它是无限大的,所以抽取到任何实数的概率都是 0)。
群的力量:Diffie-Hellman 密钥交换
群是强大的数学对象,让我们看看群在密码学中的一个重要用例。Diffie-Hellman 密钥交换允许两方,例如 Alice 和 Bob,彼此交换一些秘密 s ,而不被对手窃听而获得这个秘密。
- Alice 和 Bob 公开商定一个生成元 g 和群

- Alice 随机挑选一个私有数字 a ,计算出
 并发送给 Bob
并发送给 Bob - Bob 随机选取一个私有数字 b ,计算出
 并发送给 Alice
并发送给 Alice - Alice 计算

- Bob 计算

译者注:原文写作如此,但似应为
和
请注意,根据乘方规则,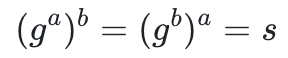 ,即 Alice 和 Bob 都能计算出一个共享的秘密!现在假设一些对手 A 试图在没有获得 a 或 b 的情况下也计算出秘密 s ,他们能做到吗?让我们通过一个简单的群例子
,即 Alice 和 Bob 都能计算出一个共享的秘密!现在假设一些对手 A 试图在没有获得 a 或 b 的情况下也计算出秘密 s ,他们能做到吗?让我们通过一个简单的群例子 来回答这个问题,在
来回答这个问题,在 中,整数模数 p 是一些非常大的素数。A 想要计算出
中,整数模数 p 是一些非常大的素数。A 想要计算出 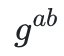 ,他必须找到一个
,他必须找到一个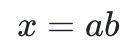 ,以便
,以便 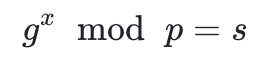 。这就是所谓的离散对数问题(Discrete-Logarithm Problem)。
。这就是所谓的离散对数问题(Discrete-Logarithm Problem)。
对于较大的素数 p ,要找到 x 这样的解在计算上是不可行的。这是一个被普遍认可的难题,自希腊博学家 Eratosthenes(见 Eratosthenes 筛法)以来,素数因式分解就一直是一个困难的问题。事实上,2000 年来没有人破解过这个系统!离散对数的难解性是现代密码学的核心基础,包括应用于像 RSA 这样的公钥密码系统的发展。
译者注:原文如此,但 RSA 公钥密码体系的安全性应是与大整数分解有关,和离散对数问题相关的公钥密码体制应为 ElGamal 加密方案。

这个例子引出了密码系统中另一个常用的想法 :计算 Diffie-Hellman 假设,即在给定 和
和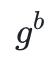 的情况下,对手要计算
的情况下,对手要计算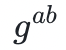 在计算上是不可行的。实际上,除非某人同时知道 a 和 b,否则几乎不可能知道秘密
在计算上是不可行的。实际上,除非某人同时知道 a 和 b,否则几乎不可能知道秘密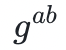 。
。
椭圆曲线 (ECs:Elliptic curves) 是现代密码学的核心部分,它们并不是一个新概念,从比特币开始它们就在区块链中广泛使用。椭圆曲线只是一种特殊类型的满足 Diffie-Hellman 假设的群。
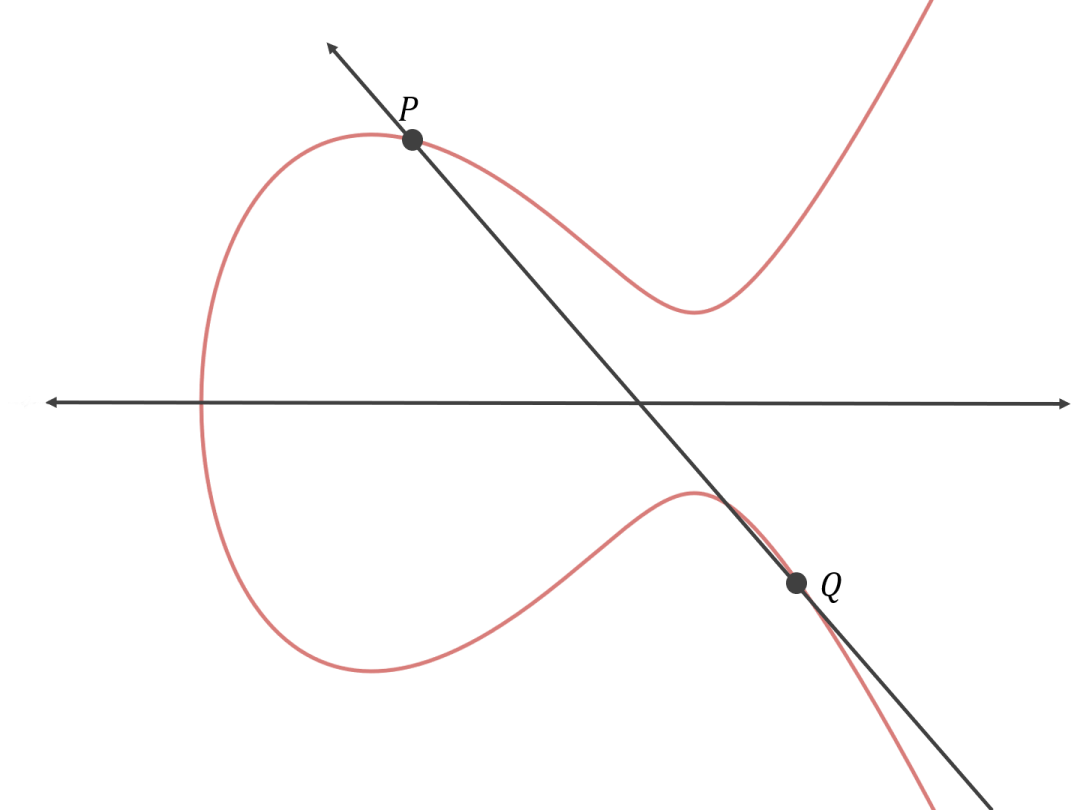
椭圆曲线背后的理论涉及很多数学,我们可以用文字总结一下椭圆曲线背后的直觉 。一个椭圆曲线是一个点的集合,这些点通过以下操作构成一个群:如上图所示,在椭圆曲线上给定两个不同的点 P 和 Q ,连接这两个点的线正好与椭圆曲线相交于另一个点 R ;我们将 R 穿过将曲线分成两半的轴,得到一个也在曲线上的点 S ,我们定义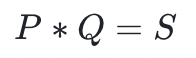 。
。
一个椭圆曲线密码系统是通过选择一个大小为 m(素数)的有限域、一个曲线方程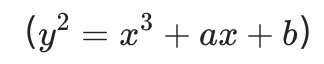 和曲线上的一个公共点 P 来定义的 。私钥是一个 t < m 的数字,而公钥是通过 * 运算符将 p 应用于自身 t 次,即通过
和曲线上的一个公共点 P 来定义的 。私钥是一个 t < m 的数字,而公钥是通过 * 运算符将 p 应用于自身 t 次,即通过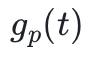 将 p 应用于自身 t 次。在只知道某人公钥的情况下,要计算他的私钥 t 会非常困难,因为:
将 p 应用于自身 t 次。在只知道某人公钥的情况下,要计算他的私钥 t 会非常困难,因为:
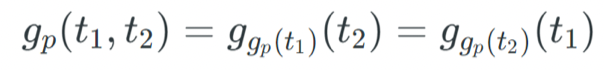
因此,分别拥有私钥 t1 和 t2 的两方 Alice 和 Bob 有可能共享一个秘密,而其他人在不知道 t1 和 t2 的情况下是无法计算出这个秘密的。这完全满足了 Diffie-Hellman 密钥交换的条件。
这意味着什么?——我们可以使用相对较小的密钥来实现与 RSA 等其它密码系统类似的安全保证。
素域
域可以是实数、有理数或复数。有限域是一个仅包含有限数量元素的集合,我们为其定义了加、减、除和乘等运算,但如何实现这一点呢?如果你把一个域中的元素相加或相乘若干次,你应该得到一个此域中的数字。举一个具体的例子:假设 1 是域 的一个元素,我们可以将 1 与其自己相加 n 次(n 是素数)。我们如何保证这个计算结果返回的元素仍然属于这个域的成员元素?一种方法是简单地在计算的最后加入一个余数函数
的一个元素,我们可以将 1 与其自己相加 n 次(n 是素数)。我们如何保证这个计算结果返回的元素仍然属于这个域的成员元素?一种方法是简单地在计算的最后加入一个余数函数
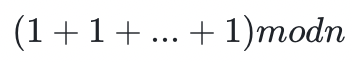
更常见的情况是,如果一个操作(加法/乘法)被应用于某个元素 e 上 m 次,其中 m > n ,你将总是得到一个属于这个域的成员元素 e′!更有数学经验的读者可能会注意到,任何域在本质上都是一个满足某些规则的附加运算的群,但我们在这篇入门文章中不会深入探讨这些细节。
多项式
多项式在密码学和许多密码学证明系统提供的安全保证中扮演着至关重要的角色。
定义:在某个有限域
上,总阶为 d 的一元多项式 p 定义如下:
译者注:原文如此,似应为
多项式在密码学中有用的一个直观原因是,它们能够非常简洁地表示大量的信息。想象以下创建一个数字表这样具体的例子。在第一列中,你开始按顺序写下自然数(即从 1 开始的整数,这称为求值域。现在,从第二列开始写下实数轴上的随机数字。如果我们在这些点上进行插值,我们就可以创建一个可以一次性表示所有这些信息的多项式!实际上,我们可以把多项式当作某个求值域上的大型真值表的连续表示。
Schwarz-Zippel 引理
在这里多项式可以派上用场。Schwarz-Zippel 引理是确保许多加密证明系统可靠性的核心工具。
定义:给出两个不同的单变量多项式 p ,q 的阶在某个有限域
上小于等于 d。
这意味着如果两个低阶多项式不相等,它们在域内的几乎所有的点都不一致。通常加密证明系统会将一些计算(编写是一些更高层级的抽象——比如 Solididity 代码)转换为多项式,然后我们可以利用这个引理来确保协议的可靠性。
一些密码学工具
我们希望加密证明系统具有两个主要属性:(1)完备性;(2)可靠性。基于确定性的验证者,完备性和可靠性定义如下:
- 完备性:给出一个验证者总是能够接受的真实声明
- 可靠性:验证者不应接受任何错误声明。
现在允许验证者抛一些硬币(即使得验证者非确定性)。
- 完备性:验证者被真实声明说服的概率(通常我们希望是 1)
- 可靠性:对于所有证明者(也包括恶意的),验证者接受错误声明的概率应该很低。
这里的区别非常细微,但对密码证明系统至关重要——随机性允许我们构造可以高效运行的证明系统(通常这意味着验证者可以在多项式时间内运行)。
Sumcheck 协议
Sumcheck 协议是交互式证明系统的基本构建模块之一。在本质上,这个协议是定义在如下场景:一个证明者想要向一个验证者证明它关于如下求和的知识
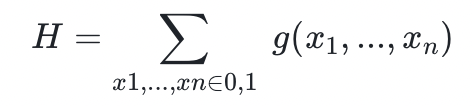
其中 g 是 n 个变量的多项式。我们假设验证者可以预言访问(即他们可以低成本地求值)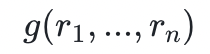 。证明者和验证者希望相对有效地参与这一过程,而
。证明者和验证者希望相对有效地参与这一过程,而 Sumcheck 允许他们以迭代的方式进行。下面是对 Sumcheck 协议的一个直观描述 。
我们希望验证者利用交互和随机性,而不是对多项式求所有可能的值(指数时间问题)。通过将每个变量绑定到域中的某个随机元素,我们可以有效地在协议的每一轮中 “剥离” 每个操作符。首先,证明者提供一个多项式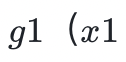 表示为:
表示为:

或者提供除第一个变量以外的其余所有变量的总和(第一个变量是自由的)。我们可以看到 H 是 g1 在 X1 所有可能的值上的总和,事实上,验证者检查是否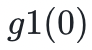 和
和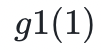 的总和确实等于 H 。
的总和确实等于 H 。
如果这不是真的,那么显然证明者不知道这个和,但验证者可以如此陈述。如果这是真的,验证者不能确定证明者知道这个和——证明者可能只是幸运地挑选了一个在 X1 所有值上的和恰好等于 H 的 g1 ——但是证明者知道 H 的概率已经增加。
验证者随后对 X1 随机采样一个值 r1,然后把它发送给证明者,证明者现在的任务是发回一个表示所有变量的和(除第一个变量)的多项式 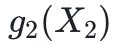 ,其中,第一个变量被设为 r1,第二个变量是固定的。我们可以看到这里的迭代模式:验证者将检查从上次迭代中正确提供的
,其中,第一个变量被设为 r1,第二个变量是固定的。我们可以看到这里的迭代模式:验证者将检查从上次迭代中正确提供的 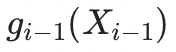 是否等于本次迭代中提供的
是否等于本次迭代中提供的 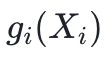 对
对 所有可能值的和。
所有可能值的和。
如果在任何一点上证明者不能提供一个正确的多项式,它将被验证者拒绝;每次它成功提供正确的下一个迭代时,它知道 H 的概率就会增加,而不只是幸运。
最后,如果证明者正确地提供了最后一次迭代(多项式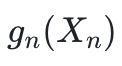 ),验证者就会得出结论:证明者具有非常高的概率知道 H 。
),验证者就会得出结论:证明者具有非常高的概率知道 H 。
为什么这很有用呢?
- 现在我们了解了
Sumcheck,让我们把它当作一个黑箱算法,用来证明某些计算实际上是有效的。 - 使用
Sumcheck的高级方法是用布尔超立方体上的和来重写你想设计协议里的一些计算。通过将我们的问题还原为Sumcheck的实例,我们就可以非常轻松地应用它了!
GKR 协议
让我们来看看 Sumcheck 的一个具体用例。GKR 协议是一个迷人的、聪明的协议,用于有效地验证可被表达为低深度算术电路的计算。这是最早的尝试之一,提出一个可以验证一类非常普遍的计算的系统(不仅仅是布尔超立方上的和)。顺便说一句,它使用了 Sumcheck 作为算法的支柱。
这里有一个基本结构--我们有一些可以用不同层来表达的计算。直观地说,我们可以让验证者只是重新运行电路的计算,并检查验证者的输出是否与声明的输出一致。但这非常低效。相反,让我们尝试利用电路的结构来降低验证者的时间复杂性。
基本的直观判断是这样的:我们把对电路第 i 层的声明还原为对第 i+1 层的声明 。我们按照这个过程进行归纳,把声明一直还原到只是在一组随机点上评估一个多项式,而不是评估整个电路。
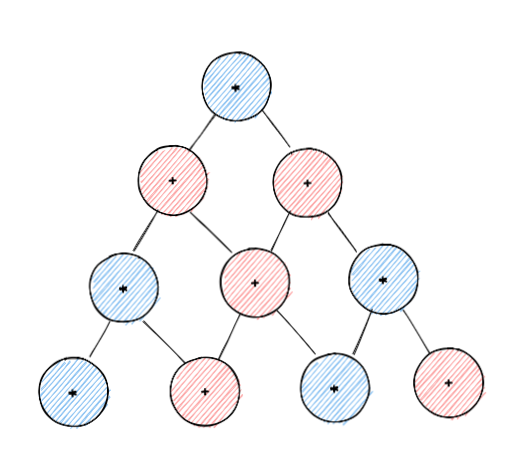
算术电路到底是什么
我们已经讨论了一些数学对象,如对建立加密证明系统有用的多项式,但我们还没有谈及我们如何实际计算它们。算术电路是一种简单明了的方式来表示评估多项式时涉及的计算。算术电路类似于计算机和电子产品中使用的逻辑电路。在电子芯片中,我们有一堆相连的门(AND,OR,NOT,XOR,等等)。我们给这些门一些输入,并将某个门的输出作为下个门的输入。但是,我们用加法和乘法等算术运算取代了这些逻辑运算符。我们得到如下的东西:
多项式承诺方案
多项式承诺方案(PCS:Polynomial Commitment Schemes)对加密证明系统的运作极为重要。在一个非常基础的层面上,它确保证明者在与验证者互动时不能作弊,也就是说,证明者不能根据验证者正在抽取的随机点来改变他之前的信息,我们把这个属性称为非自适性(non-adaptivity)。前文提及的 Sumcheck 协议说到,我们希望证明者在验证者发送随机点之前对多项式做出承诺(承诺方案是确保证明者行为诚实的一种有力方式)。我们将在后面的文章中看到,多项式承诺方案在确保加密证明系统的安全性方面起着关键作用。
如下是这个方案的工作原理:
- 证明者对一些参考字符串进行承诺
- 验证者如何知道证明者确实承诺了这个多项式?
- 验证者要求证明者在某个随机点计算多项式
- 证明者在椭圆曲线上的某个点发回多项式的计算值
结语
在这篇文章中,我们描述了一些核心的数学和密码学工具,以帮助你了解和评估密码学证明系统。我们希望你能发现这篇文章既令人兴奋又有助于解开一些通常很神秘的 "月球数学",这些 “月球数学” 涉及到构建你最喜欢的私有 L1、可扩展的 L2 或零知识驱动的应用程序。有了这个背景,希望你能更好地准备好去挖掘其它证明系统的一些内部工作原理。
免责声明:作为区块链信息平台,本站所发布文章仅代表作者及嘉宾个人观点,与 Web3Caff 立场无关。本文内容仅用于信息分享,均不构成任何投资建议及要约,并请您遵守所在国家或地区的相关法律法规。


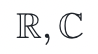
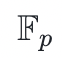 ,其中 p 是素数
,其中 p 是素数
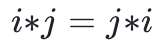
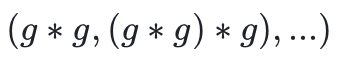 对其重复应用 g ,那么我们就可以抽取到群中的每一个元素。
对其重复应用 g ,那么我们就可以抽取到群中的每一个元素。
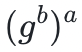
 上,总阶为 d 的一元多项式 p 定义如下:
上,总阶为 d 的一元多项式 p 定义如下: