何為大整數分解? 如何實踐大整數分解演算法?
封面:Photo by Shubham Dhage on Unsplash
大整數分解
1977 年,基於大整數分解難題的密碼體系 RSA 誕生,命名自 Ron Rivest、Adi Shamir 和 Leonard Adleman 三位提出者姓氏的首字母。 RSA 演算法在公鑰密碼學上作出重要貢獻並對全世界產生重要影響,三位提出者於 2002 年獲該年度圖靈獎。 整數分解問題是當今幾乎所有公鑰密碼安全性領域中最重要的課題之一。
RSA 演算法的安全性依賴於大整數分解難題,即
將一個大整數分解成若干大素因數的乘積。

針對小因數的幾種典型的大整數分解演算法有:
- Pollard's rho 演算法
- Pollard's p-1 演算法
- ECM 演算法(Lenstra elliptic curve factorization/elliptic-curve factorization method)
此次我們將介紹 Pollard's p-1 演算法、ECM 演算法與 ECM 演算法的一個具體實踐 —— GMP-ECM。
Pollard's p-1 演算法


ECM 演算法

對於這個方法的改進,ECM 方法在 Pollard's p-1 的基礎上引入了隨機的橢圓曲線,將原本的乘法群轉換為橢圓曲線的點構成的群。 橢圓曲線方法是一種基於數論的演算法,利用橢圓曲線上的點的性質和運算規則,尋找滿足一定條件的因數。
演算法概述

一種 ECM 實現 —— GMP-ECM
GMP-ECM 的實現基於原有的 ECM 方法進行了優化。

Stage 1
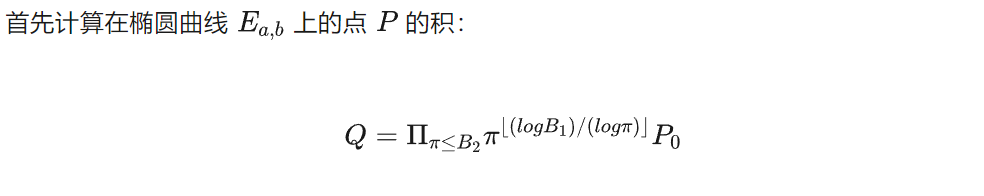
在 Stage 1 的計算中,GMP-ECM 優化了橢圓曲線的選取與計算。
随机的椭圆曲线生成

椭圆曲线运算
在 GMP-ECM 中使用 Montgomery’s 形式的椭圆曲线,在求点的乘法或加法过程遵循如下规则:

Stage 2

Stage 2 的主要思想為中間相遇(meet-in-the-middle)策略:

演算法複雜度

示例
N=0xA2862FB145AC7CE580E0BFF3CEFF42646050F8C611D36A3026E6EFB433B5CDD9EEFBA893E3F25C23A4951BA20992680162934CBDB6876CC791738C140C6EA6EC82938F7E18C5F0760367CF20883DCAB1D6885E222BBC7A1B5D434FD9FC148E387FA9AD69CE708FDDDE3E963F9AB2AF2046A37D7DBA21BC92E6F2A631C3E7770C77C95FAD6F1DC60D9F0645AEF2CC5D03D2151E35443FE0F90F1E2EAE58489C4450C8281EDCC58DDB409C306797C616954ACABCE4881E40ABDD2689A9F7596F29CD5CB42C752DA9306E7DB87CAC8957E3CA165421CF9E1B7220759A10588B386E33FD8E762E92C9F79D50150EF5FCA5F411DE23B8DFFE47A95D48ADDCF4797565呼叫解析工具(https://github.com/Safeheron/integer-factorization)使用 GMP-ECM 方法分解:
ecm -c 2 25e4 1.3e8 -mpzmod threads: 2 mod: 1A2862FB145AC7CE580E0BFF3CEFF42646050F8C611D36A3026E6EFB433B5CDD9EEFBA893E3F25C23A4951BA20992680162934CBDB6876CC791738C140C6EA6EC82938F7E18C5F0760367CF20883DCAB1D6885E222BBC7A1B5D434FD9FC148E387FA9AD69CE708FDDDE3E963F9AB2AF2046A37D7DBA21BC92E6F2A631C3E7770C77C95FAD6F1DC60D9F0645AEF2CC5D03D2151E35443FE0F90F1E2EAE58489C4450C8281EDCC58DDB409C306797C616954ACABCE4881E40ABDD2689A9F7596F29CD5CB42C752DA9306E7DB87CAC8957E3CA165421CF9E1B7220759A10588B386E33FD8E762E92C9F79D50150EF5FCA5F411DE23B8DFFE47A95D48ADDCF4797565********** Factor found in step 2: 1021791499165844943393503 21 52761ms成功找到素因數 1021791499165844943393503。
免責聲明:作為區塊鏈資訊平臺,本站所發佈文章僅代表作者及嘉賓個人觀點,與 Web3Caff 立場無關。 本文內容僅用於資訊分享,均不構成任何投資建議及要約,並請您遵守所在國家或地區的相關法律法規。













