ECDSA 門限簽名典型算法介紹

沒有最好的，只有最合適的

作者： Cobo 密碼學團隊，Cobo Global

原用標題： Cobo 密碼知識講堂｜第三講：ECDSA 門限簽名典型算法介紹

封面： Photo by  Batyrkhan Shalgimbekov  on  Unsplash

隨著香港開始允許散戶交易數字資產，數字資產也在逐步走進每個人的生活，數字資產、數字簽名等新概念層出不窮。Cobo 密碼知識講堂計劃推出以 “門限簽名” 為主題的系列科普文章，旨在以深入淺出的方式，帶領讀者了解數字簽名中門限簽名的技術本質和應用原理。該系列科普文章每一篇內容相互獨立又互相補充，涵蓋門限簽名的概念及典型應用、ECDSA 門限簽名的設計及發展現狀、Schnorr 門限簽名的設計及發展現狀、基於門限簽名的賬戶體系構建，以及層級化門限簽名設計等多個該領域的熱點和難點問題，力求通過對技術研究的深層次剖析和解讀，讓讀者對門限簽名領域有更加深刻的理解。

《Cobo 密碼知識講堂｜第一講：門限簽名的概念與應用》

《Cobo 密碼知識講堂｜第二講：ECDSA 算法及其門限化設計介紹》

本講概述：本期課程介紹 ECDSA 門限簽名，首先對當前已有的 ECDSA 門限簽名算法的技術路線進行歸納和總結，繪製其技術發展的 “科技樹”；隨後，針對 ECDSA 門限簽名算法實現的不同技術途徑，進行針對性的介紹，闡述其設計原理、核心組件和技術迭代過程；最後，結合學術研究基礎和產業界業務經驗，給出 ECDSA 門限簽名算法使用的相關建議，以供參考

Part 1：ECDSA 門限簽名 “科技樹”

隨著比特幣等加密數字貨幣的迅速發展，ECDSA 門限簽名算法已經得到學術界和產業界的重點關注，充分的科研資源投入使得近些年來湧現出大量研究成果。這些科研成果的設計目標是一致的，即具備高安全性、低計算與通信複雜度和計算過程可審計的 ECDSA 門限簽名算法。然而它們的設計重點、技術途徑、使用的密碼學技術各不相同，既存在一定程度的 “技術繼承”，也具備 “技術獨立” 的特徵。在充分研究的基礎上，我們對 ECDSA 門限簽名算法的 “科技樹” 進行梳理，澄清不同研究成果之間的技術關聯關係和繼承關係，具體見圖 1。

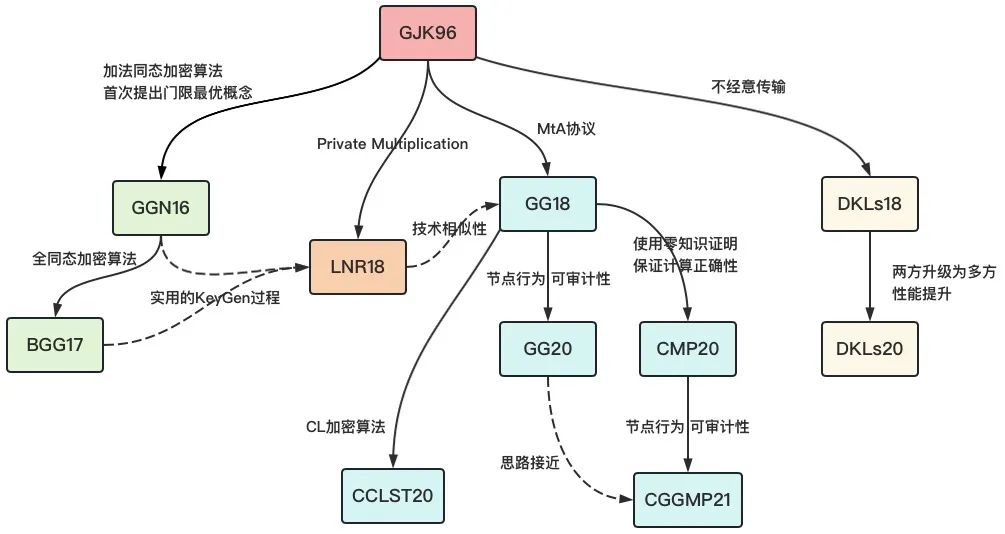
整體而言，GJK96 是第一個 ECDSA 門限簽名方案，其設計思路也非常直觀樸素，而且並未滿足門限最優的性質。以 GJK96 為基礎，圍繞門限最優、高效性、可審計性等設計目標，出現了一系列的技術方案。以實現門限最優的技術途徑為基本分類維度，這些方案大致可以分為四個技術體系：基於分佈式同態加密、基於 MtA 協議、基於 Private Multiplication 協議和基於不經意傳輸。在下一部分，我們對這四個技術體系的代表性方案進行詳細介紹。

Part 2：典型 ECDSA 門限簽名算法介紹 GJK96：ECDSA 門限簽名方案的先驅

在 GJK96 中，私鑰 和簽名隨機數 是以秘密碎片的形式存在於 個節點，每個節點 保存碎片 和 。而簽名過程中 的碎片是直接將 和 相乘得到，導致秘密分享多項式的次數由 提升為（見圖 2），從而不具備門限最優的性質，即恢復私鑰僅需 個節點參與，但是完成門限簽名則需 個節點。GJK96 作為首個 ECDSA 門限簽名方案，扮演了 “吃螃蟹” 的角色，具有先驅意義。然而由於其非門限最優的缺陷，使得在實際賬戶管理中需要部署比安全門限（即）更多的服務器，在提高了運營成本的同時，也增加了賬戶安全風險，並不適用於當前場景需求。

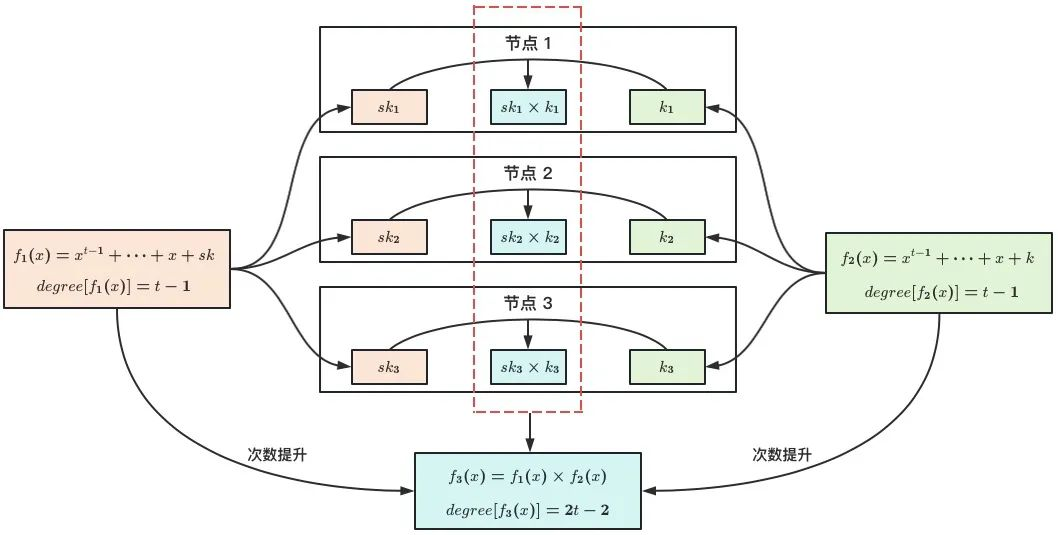
GGN16 / BGG17：基於分佈式同態加密的 ECDSA 門限簽名方案

GGN16 首次提出了 “門限最優（Threshold Optimality）” 的概念，並設計了首個 ECDSA 門限最優簽名算法。其設計思路（見圖 3）在於將計算簽名所需要的參數通過加法同態加密算法進行加密，簽名過程是在密態下進行並最終生成簽名的密文，最後所有節點合作解密得到簽名的明文數據。而其中的關鍵步驟，在於所有節點通過可信第三方或者公共可驗證算法生成一套加法同態加密算法參數，加密公鑰公共可知，解密私鑰則以碎片的形式分佈在各節點。BGG17 與 GGN16 的設計思路類似，其改進在於將加密算法由加法同態加密算法替換為一階同態加密算法，使得對加密後的參數進行任意次加法以及深度為 1 的乘法運算均能保證同態性，從而降低節點交互的次數，由 6 輪降低為 4 輪。

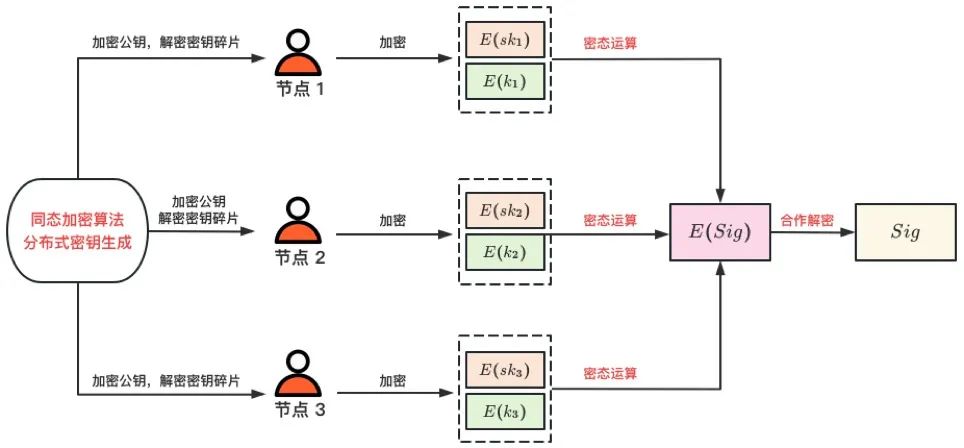
基於分佈式同態加密的 ECDSA 門限簽名方案雖然實現了門限最優的性質，但是也存在非常致命的問題，即可實現性/實用性未知，因為節點個數超過 2 時，如何分佈式生成一個同態加密算法（如 Paillier Encryption）的密鑰，是一個不確定的問題。

GG18 / GG20 / CCLST20 / CMP20 / CGGMP21：基於 MtA 協議的 ECDSA 門限簽名方案

基於 MtA 協議的 ECDSA 門限簽名是當前非常主流的一種實現方式，已經大範圍地被應用到實際的業務場景中。該方案的核心在於基於 MtA 協議（Multiplication to Addition）實現了 的計算過程，同時沒有引起秘密分享多項式次數的升高，滿足了門限最優的性質。MtA 協議基於 Paillier 同態加密算法實現，協議輸入是乘法秘密碎片 和 ，滿足 ，協議輸出是加法秘密碎片 α 和 β ，滿足 αβ ，具體運行流程見圖 4。

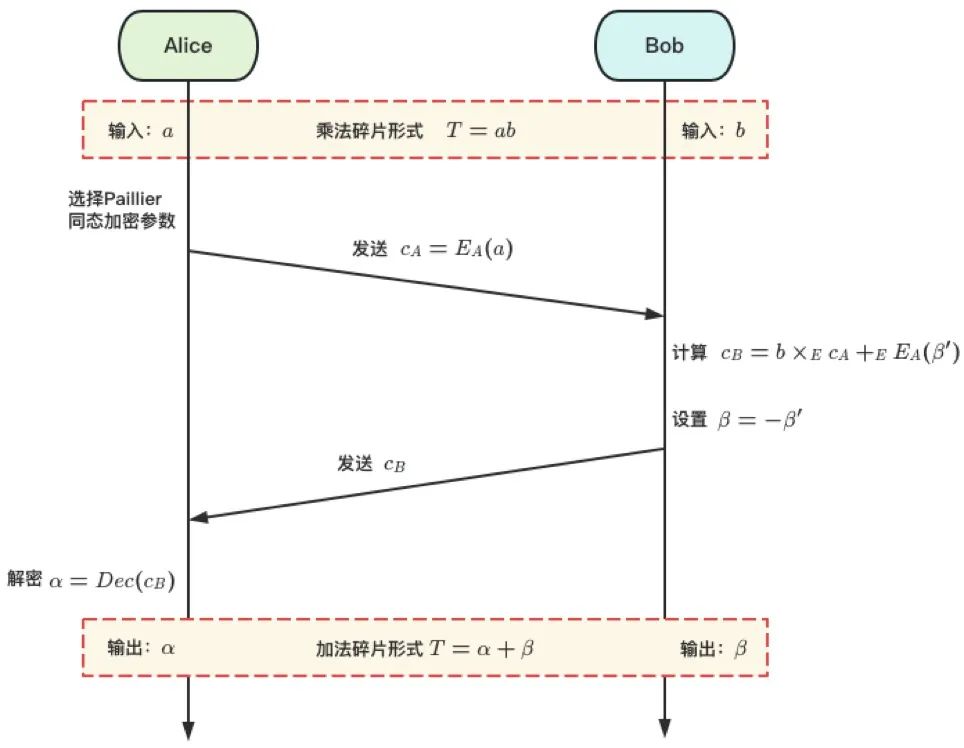
GG18 是首個基於 MtA 協議實現的 ECDSA 門限簽名方案。GG20 是對 GG18 的改進，一方面實現了可驗證終止性（Identifiable Abort），另一方面將簽名的過程拆分為預處理階段（Preprocess Stage）和在線階段（Online Stage），線上僅需一輪交互即可完成簽名。CCLST20 是將 GG18 中使用的 Paillier 同態加密算法替換位 CL 同態加密算法，從而避免了由 Paillier 模數和 ECDSA 模數不一致導致的、需要引入大量零知識證明完成範圍證明的計算負荷。CMP20 則是將關注點放在計算過程的安全性保障上，通過在各個步驟引入對應的零知識證明，從而保證簽名過程的安全性，避免了由於簽名失敗而導致的敏感信息洩漏風險，是對 GG18 中籤名結果正確性驗證方法（即步驟 5A-5E）的有效提升。CGGMP21 是對 CMP20 的提升類似於 GG20 對 GG18 的提升，即增加了節點行為的審計性，給出兩個不同的解決方案，即一個方案是 4 輪交互和 的計算複雜度，另一個方案是 7 輪交互和 的計算複雜度。

LNR18：基於 Private Multiplication 協議實現的 ECDSA 門限簽名方案

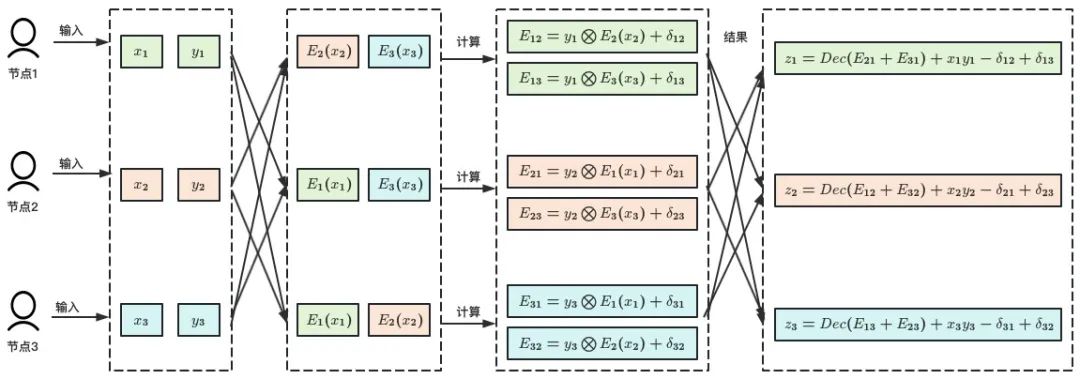
LNR18 和 GG18 有很深的淵源，二者都是在 CCS18 上同期發表的論文，因此技術途徑具備非常強的相似性，但是側重點又不同。LNR18 的設計出發點在於對 GGN16 和 BGG17 的 KeyGen 階段實用性的質疑，即分佈式生成一個同態加密算法密鑰是困難的。基於這一認識，LNR18 設計了一個 “雙層” 協議，上層是將 Paillier 同態加密算法替換為 ElGamal 算法，由於 ElGamal 算法非常強的線性特徵，因此其分佈式密鑰生成實現簡單。但是需要強調的是，協議中對 ElGamal 算法的使用是在指數上執行（ElGamal in-the-exponent），因此並不會直接解密得到明文，而是得到明文的橢圓曲線倍點，從而完成計算過程正確性的驗證，類似於 GG18 的 5A-5E 過程。下層則是協議的核心，基於 Private Multiplication 協議完成簽名的實際計算過程。Private Multiplication 協議的工作流程見圖 5，其基本設計思路與 MtA 協議類似，都依賴於同態加密算法實現，但是對擾動項的處理方式不同，Private Multiplication 協議是在形成最終輸出前統一消除，而 MtA 協議則是在兩兩交互過程中消除。

DKLs18 / DKLs20：基於不經意傳輸實現的 ECDSA 門限簽名方案

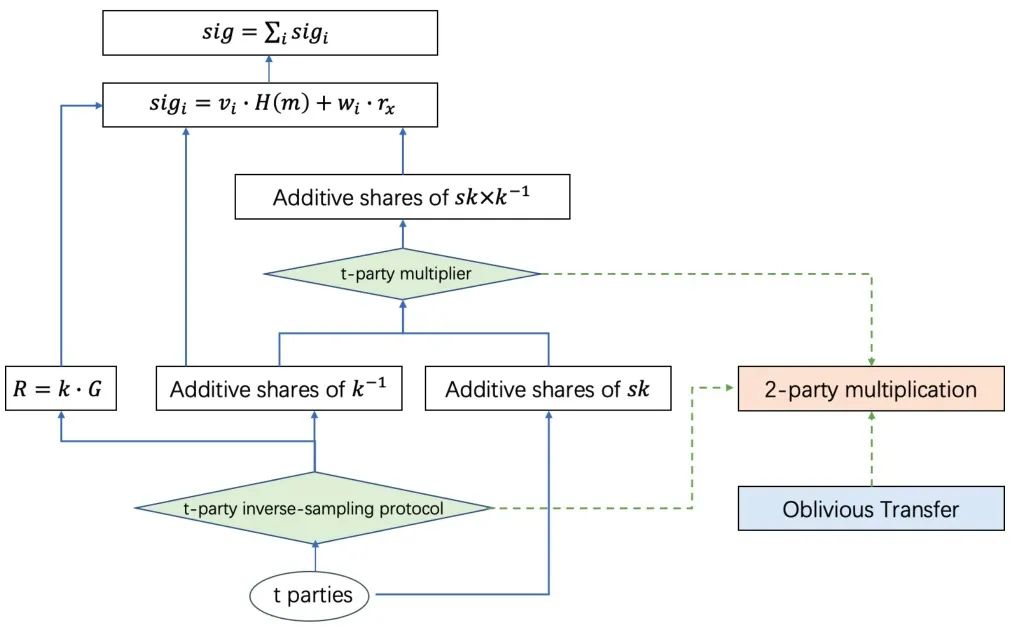
DKLs18 和 DKLs20 是基於相關不經意傳輸（Correlated Oblivious Transfer，簡稱 COT）實現的 ECDSA 門限簽名方案，與之前的技術途徑存在比較明顯的差異，當然這不代表其底層的密碼學技術不同，因為 COT 的實現也是依賴同態加密。DKLs18 是針對兩方的 ECDSA 門限簽名方案，而 DKLs20 在其基礎上了改進，擴展為多方的 ECDSA 門限簽名方案，同時對通信和計算過程進行了優化，實現 40% 性能提升。DKLs20 的協議流程見圖 6，核心組件為 2-Party Multiplication，其功能類似於 MtA 協議，是基於 COT 實現。基於 2-Party Multiplication，實現了 t-party Inverse-sampling 協議和 2-party Multiplier 協議，分別完成求逆運算和乘法運算，最終實現完整的簽名過程。

Part 3：ECDSA 門限簽名算法使用攻略

本文內容共涉及到 11 種 ECDSA 門限簽名算法，還有很多其他算法沒有體現，此外隨著學術界的持續研究，可以預見未來會有更多的門限簽名算法出現。那麼究竟該選擇哪個 ECDSA 門限簽名算法作為數字資產多方管理的解決方案？是一個值得思考的問題。基於學術研究基礎和產業界業務經驗，本文給出如下建議供參考。

沒有最好的，只有最合適的

不同的 ECDSA 門限簽名算法在設計之初，就有不同的側重點，或是側重效率的提升（如優化通信輪數），或是側重安全證明（如降低安全假設），或是側重節點行為可審計性（如增加額外可驗證數據）。無論是哪個側重點，都是在不同性質之間做 Tradeoff。因此，選擇 ECDSA 門限簽名算法的核心，還是要把握自身需求，選擇最適配的算法，而非唯新論、唯複雜論。Cobo 對 ECDSA 門限簽名算法的選擇，是以整個領域的研究成果為基礎，結合實際業務和客戶的需求，綜合考慮安全和性能，最終選擇最合適的方案。

保持對技術的敬畏之心

ECDSA 簽名算法本身是 Threshold Unfriendly 的，因此其門限化的設計比其他簽名算法（如 Schnorr、BLS）要復雜很多。具體體現在兩個方面：一個是使用到的密碼學技術複雜，如同態加密、零知識證明、不經意傳輸等；另一個是攻擊模型複雜，複雜的算法帶來的是複雜的攻擊手段，因此需要謹慎設計，避免安全漏洞。目前大部分的算法都提供了形式化證明，可以理解為可證明安全的，如此精細的算法，不存在任何冗餘的操作和組件。之前就出現過類似的案例 ，即工程實現的時候遺漏了論文中關於 Paillier 加密算法的公共參數 N 的零知識證明，最終導致在簽名交互過程中誠實節點私鑰碎片洩漏的風險。因此在實際使用 ECDSA 門限簽名算法時候，要保持對技術的敬畏之心，嚴格按照協議標準實現，避免出現安全風險。

參考文獻

1. Gennaro R, Jarecki S, Krawczyk H, et al. Robust threshold DSS signatures[C]//International Conference on the Theory and Applications of Cryptographic Techniques. Springer, Berlin, Heidelberg, 1996: 354-371.
2. Gennaro R, Goldfeder S, Narayanan A. Threshold-optimal DSA/ECDSA signatures and an application to Bitcoin wallet security[C]//International Conference on Applied Cryptography and Network Security. Springer, Cham, 2016: 156-174.
3. Boneh D, Gennaro R, Goldfeder S. Using level-1 homomorphic encryption to improve threshold DSA signatures for bitcoin wallet security[C]//International Conference on Cryptology and Information Security in Latin America. Springer, Cham, 2017: 352-377.
4. Gennaro R, Goldfeder S. Fast multiparty threshold ECDSA with fast trustless setup[C]//Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security. ACM, New York, NY, 2018: 1179-1194.
5. Gennaro R, Goldfeder S. One Round Threshold ECDSA with Identifiable Abort[J]. IACR Cryptol. ePrint Arch., 2020, 2020: 540.
6. Castagnos, G., Catalano, D., Laguillaumie, F., Savasta, F., Tucker, I. Bandwidth-Efficient Threshold EC-DSA[C]//Public-Key Cryptography – PKC 2020. Lecture Notes in Computer Science(), vol 12111. 
7. R. Canetti, N. Makriyannis, and U. Peled. Uc non-interactive, proactive, threshold ecdsa[J]. IACR Cryptol. ePrint Arch., 2020, 2020: 492.
8. Canetti R , Gennaro R , Goldfeder S , et al.UC Non-Interactive, Proactive, Threshold ECDSA with Identifiable Aborts[C]//2020 ACM SIGSAC Conference on Computer and Communications Security.
9. Y. Lindell and A. Nof. Fast secure multiparty ECDSA with practical dis- tributed key generation and applications to cryptocurrency custody[C]//ACM CCS 2018, pages 1837–1854.
10. J. Doerner, Y. Kondi, E. Lee, and a. shelat. Secure two-party threshold ECDSA from ECDSA assumptions[C]//In 2018 IEEE Symposium on Security and Privacy, pages 980–997. 
11. J. Doerner, Y. Kondi, E. Lee, and a. shelat. Threshold ECDSA from ECDSA assumptions: The multiparty case[C]//In 2019 IEEE Symposium on Security and Privacy, pages 1051–1066.
12. BitGo Wallet Zero Proof Vulnerability: Technical Report.[EB/OL]. (2023-03-17) [2023-06-10].https://www.fireblocks.com/blog/bitgo-wallet-zero-proof-vulnerability/

免責聲明：作為區塊鏈信息平台，本站所發布文章僅代表作者及嘉賓個人觀點，與 Web3Caff 立場無關。文章內的信息僅供參考，均不構成任何投資建議及要約，並請您遵守所在國家或地區的相關法律法規。