本文將介紹基於橢圓曲線的數字簽名算法 Ed25519 的實現原理與可延展性問題。
作者:阿為
Ed25519 是一個基於橢圓曲線的數字簽名算法,它高效,安全且應用廣泛。TLS 1.3, SSH, Tor, ZCash, WhatsApp 和 Signal 中都使用了它。本文主要講解以下幾點:
1. 介紹一點群論知識,目的是讓大家對 Ed25519 和其可延展性問題的原理有一種直覺。若想深入理解,還需參考其他資料;
2. 針對 rust 庫 ed25519-dalek 的 1.0.1 版本講解 ed25519 的實現;
3. 針對該庫的延展性問題做出解釋。
數學要點回顧
群的定義與性質
群論是抽象代數研究的內容,但抽象代數的一些思想是程序員非常熟悉的。面向對像中的繼承就是一個很好的例子,我們都知道子類繼承了父類後,就能使用父類中定義的方法。可以將抽象代數理解為對一個抽象的數據結構定義了一些性質,由這些性質推導出來的定理對於所有的子類都成立。
沿用剛剛的比喻,來看看群(group)這個數據結構是如何定義的。
一個群由一個操作(任何的二元操作用 o 記)和一些元素構成,同時滿足如下性質:


拉格朗日定理
現在介紹一個非常有意思的定理,這個定理的推導在文末引用的視頻中。
“群的階能被子群的階整除。”
為什麼說這個定理有意思呢,不僅僅因為它的證明過程串起了剛剛介紹的許多知識,還因為下面的結論:

Ed25519 的實現
現在我們來講 Ed25519,它是 EdDSA 算法的其中一種。EdDSA 有 11 個參數(https://datatracker.ietf.org/doc/html/rfc8032#autoid-3),這些參數的具體選擇對於算法的安全和性能有很大的影響。Ed25519 的具體選擇請參看鏈接(https://datatracker.ietf.org/doc/html/rfc8032#autoid-9)。
另外,值得一提的是這套算法用到了一個叫 Curve25519(https://datatracker.ietf.org/doc/html/rfc7748#autoid-5)的橢圓曲線。對於橢圓曲線,我們只需知道,它上邊有很多很多點,這些點相加能得到新的點,新的點還是在曲線上。這些點和這個加法能形成一個群。注意這裡的橢圓曲線加法(https://www.wikiwand.com/en/Elliptic_curve_point_multiplication)是有特殊定義的。


這是個交互式的算法,但是沒關係,有一個技巧叫做 the Fiat – Shamir heuristic(https://link.springer.com/chapter/10.1007%2F3-540-47721-7_12),它可以把任意的交互式算法轉化成非交互式的算法。最終我們會用非交互式算法。
數字簽名算法都會給我們如下 API:
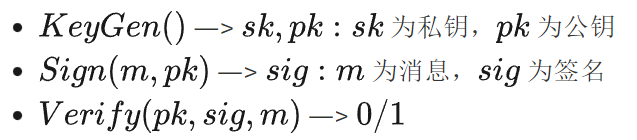
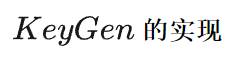
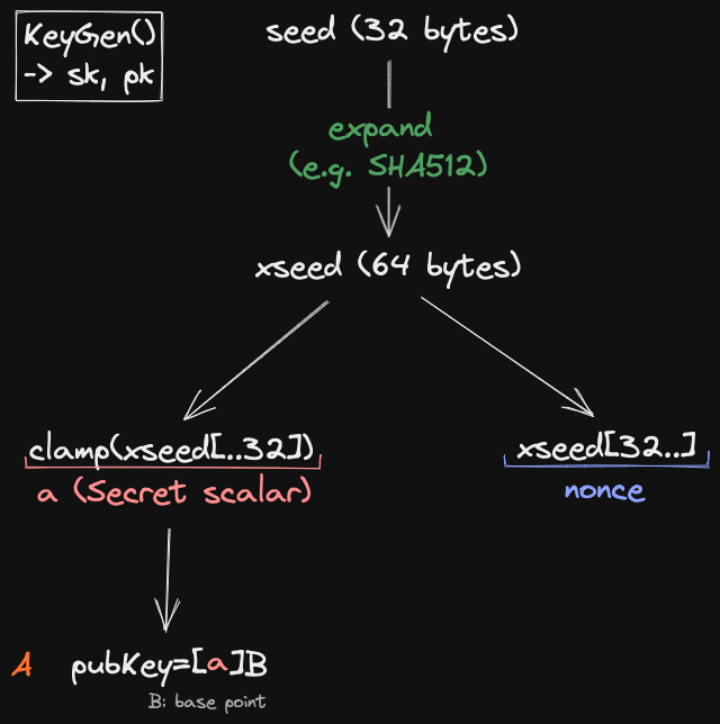
輸出一個私鑰和一個公鑰:
1. 隨機生成一個 seed(https://github.com/dalek-cryptography/ed25519-dalek/blob/97c22f2d07b3c260726b90c55cd45f34ec34a037/src/secret.rs#L167-L176),這個 seed 有 32 個字節。我們使用了一個系統自帶的密碼學安全的隨機數生成元。
pub fn generate<T>(csprng: &mut T) -> SecretKeywhere T: CryptoRng + RngCore,{ let mut sk: SecretKey = SecretKey([0u8; 32]);
csprng.fill_bytes(&mut sk.0);
sk}2. 把剛剛的 seed 擴展成 64 個字節(https://github.com/dalek-cryptography/ed25519-dalek/blob/97c22f2d07b3c260726b90c55cd45f34ec34a037/src/secret.rs#L265-L282),也就是圖中的 xseed。xseed 的低 32 字節就是我們的私鑰(aka a)。高 32 字節被稱為 nonce,後面會被用在 中,其作用類似 domain sperator。
pub struct ExpandedSecretKey { // xseed pub(crate) key: Scalar, // a pub(crate) nonce: [u8; 32], // nonce}
fn from(secret_key: &'a SecretKey) -> ExpandedSecretKey { let mut h: Sha512 = Sha512::default(); let mut hash: [u8; 64] = [0u8; 64]; let mut lower: [u8; 32] = [0u8; 32]; let mut upper: [u8; 32] = [0u8; 32];
h.update(secret_key.as_bytes()); hash.copy_from_slice(h.finalize().as_slice());
lower.copy_from_slice(&hash[00..32]); upper.copy_from_slice(&hash[32..64]);
// 这一步是 clamp lower[0] &= 248; lower[31] &= 63; lower[31] |= 64;
ExpandedSecretKey{ key: Scalar::from_bits(lower), nonce: upper, }}3. 用私鑰生成公鑰(https://github.com/dalek-cryptography/ed25519-dalek/blob/97c22f2d07b3c260726b90c55cd45f34ec34a037/src/public.rs#L54-L68)。公鑰是橢圓曲線上的一個點。具體來說,我們利用橢圓曲線的基點 來做橢圓曲線乘法,就得到公鑰。乘法中的標量則是通過對私鑰 做一次哈希得到。
pub struct PublicKey(pub(crate) CompressedEdwardsY, pub(crate) EdwardsPoint);
impl<'a> From<&'a SecretKey> for PublicKey { /// Derive this public key from its corresponding `SecretKey`. fn from(secret_key: &SecretKey) -> PublicKey { let mut h: Sha512 = Sha512::new(); let mut hash: [u8; 64] = [0u8; 64]; let mut digest: [u8; 32] = [0u8; 32];
h.update(secret_key.as_bytes()); hash.copy_from_slice(h.finalize().as_slice());
digest.copy_from_slice(&hash[..32]) PublicKey::mangle_scalar_bits_and_multiply_by_basepoint_to_produce_public_key(&mut digest) }}
fn mangle_scalar_bits_and_multiply_by_basepoint_to_produce_public_key( bits: &mut [u8; 32],) -> PublicKey { bits[0] &= 248; bits[31] &= 127; bits[31] |= 64;
let point = &Scalar::from_bits(*bits) * &constants::ED25519_BASEPOINT_TABLE; let compressed = point.compress();
PublicKey(compressed, point)}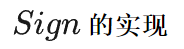

這裡可以提一下之前說的 Fiat Shamir 技巧,其實只需要把所有 Verifier 提供的隨機數替換成一個哈希函數的結果即可。具體請看代碼註釋。
pub fn sign(&self, message: &[u8], public_key: &PublicKey) -> ed25519::Signature { let mut h: Sha512 = Sha512::new(); let R: CompressedEdwardsY; let r: Scalar; let s: Scalar; let k: Scalar;
h.update(&self.nonce); h.update(&message);
r = Scalar::from_hash(h); // r 在我们交互式算法中是一个随机数,但是这里我们用了哈希。 R = (&r * &constants::ED25519_BASEPOINT_TABLE).compress(); // R = [r]B
h = Sha512::new(); h.update(R.as_bytes()); h.update(public_key.as_bytes()); h.update(&message);
k = Scalar::from_hash(h); // h = Sha512(R || A || M) s = &(&k * &self.key) + &r; // s = r + h * a,h 原本是随机数
InternalSignature { R, s }.into()}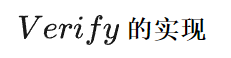

impl Verifier<ed25519::Signature> for PublicKey { #[allow(non_snake_case)] fn verify( &self, message: &[u8], signature: &ed25519::Signature ) -> Result<(), SignatureError> { let signature = InternalSignature::try_from(signature)?;
let mut h: Sha512 = Sha512::new(); let R: EdwardsPoint; let k: Scalar; let minus_A: EdwardsPoint = -self.1;
h.update(signature.R.as_bytes()); h.update(self.as_bytes()); h.update(&message);
k = Scalar::from_hash(h); // h 的计算和 sign 中一样,h=Sha512(R||A||M) R = EdwardsPoint::vartime_double_scalar_mul_basepoint(&k, &(minus_A), &signature.s); // R’ = [s]B - [h]A
if R.compress() == signature.R { // 如果 R’==R,那么验证结果为真。 Ok(()) } else { Err(InternalError::VerifyError.into()) } }}代碼地址(https://github.com/dalek-cryptography/ed25519-dalek/blob/97c22f2d07b3c260726b90c55cd45f34ec34a037/src/public.rs#L322-L355)
可延展性問題
密碼學算法的實現和使用都有非常多要注意的地方。當我們說一個數字簽名算法是安全的,一般指的是即使在攻擊者能夠獲得任意消息的簽名(Chosen Message Attack)的情況下,攻擊者仍然不能偽造簽名。Ed25519 滿足這個性質,但不代表 Ed25519 是絕對安全的。在原始的論文中也提到,可延展性問題是可以接受的,且原始的算法就有這個問題。

這樣,新構造的簽名和舊的簽名就都能被驗證成功了。延展性問題告訴我們簽名並不是相對 message 和公鑰確定,當簽名算法存在延展性問題且代碼中假設簽名是確定的情況下,就很有可能存在漏洞。


致謝
感謝領先的⼀站式數字資產⾃託管服務商 Safeheron 提供的專業技術建議。
References
[1]. https://ed25519.cr.yp.to/ed25519-20110926.pdf [2]. https://datatracker.ietf.org/doc/html/rfc8032 [3]. https://github.com/dalek-cryptography/curve25519-dalek [4]. https://github.com/dalek-cryptography/ed25519-dalek [5]. Researchers Use Group Theory to Speed Up Algorithms — Introduction to Groups免責聲明:作為區塊鏈信息平台,本站所發布文章僅代表作者及嘉賓個人觀點,與 Web3Caff 立場無關。本文內容僅用於信息分享,均不構成任何投資建議及要約,並請您遵守所在國家或地區的相關法律法規。