基本的隱身地址今天可以相當快地實施,並且可以顯著提高以太坊上的實際用戶隱私。
原文: An incomplete guide to stealth addresses
作者: Vitalik Buterin
編譯: Kyle,DeFi 之道
封面: Photo by Maria Teneva on Unsplash
特別感謝 Ben DiFrancesco、Matt Solomon、Toni Wahrstätter 和 Antonio Sanso 的反饋和審閱
以太坊生態系統中剩下的最大挑戰之一是隱私。默認情況下,進入公共區塊鏈的任何內容都是公開的。越來越多地,這不僅意味著金錢和金融交易,還意味著 ENS 域名、POAP、NFT、靈魂綁定代幣等等。在實踐中,使用整套以太坊應用程序涉及將你生活的重要部分公開給任何人查看和分析。
如何改善這種狀況已經成為一個重要的問題,這一點已得到廣泛認可。然而,到目前為止,關於改善隱私的討論主要圍繞一個特定的用例:ETH 和主流 ERC20 代幣的隱私保護轉移(通常是自我轉移)。這篇文章將描述一種不同類別的工具的機制和用例,這些工具可以在許多其他情況下改善以太坊的隱私狀態:隱身地址。
什麼是隱身地址系統?
假設 Alice 想給 Bob 一個資產。這可能是一定數量的加密貨幣(例如 1 ETH、500 RAI),也可能是一個 NFT。當 Bob 收到資產時,他不想讓全世界都知道是他得到的。想要隱藏一筆轉賬發生的事實是不可能的,特別是如果它是一個鏈上只有一個副本的 NFT,但隱藏誰是接收者可能更可行。Alice 和 Bob 也很懶惰:他們想要一個支付流程與今天完全相同的系統。Bob 向 Alice(或在 ENS 上註冊)發送某種 “地址” 編碼,編碼某人如何向他付款,僅此信息就足以讓 Alice(或其他任何人)向他發送資產。
請注意,這與 Tornado Cash 等工具提供的隱私不同。Tornado Cash 可以隱藏 ETH 或主要的 ERC20 代幣等主流可替代資產的轉賬(儘管它最容易用於私下發送給自己),但它在為不知名的 ERC20 轉賬添加隱私方面非常薄弱,並且它無法為 NFT 轉賬添加隱私。

使用加密貨幣進行支付的普通工作流程。我們想增加隱私(沒有人能知道是 Bob 收到了資產),但保持工作流程不變。
隱身地址提供了這樣的方案。隱身地址是可以由 Alice 或 Bob 生成的地址,但只能由 Bob 控制。Bob 生成並保密一個支出密鑰,並使用該密鑰生成一個隱形元地址。他將這個元地址傳遞給 Alice(或在 ENS 上註冊)。Alice 可以對該元地址執行計算以生成屬於 Bob 的隱形地址。然後她可以將她想發送的任何資產發送到這個地址,Bob 將完全控制這些資產。隨著轉移,她在鏈上發布了一些額外的加密數據(一個臨時公鑰),幫助 Bob 發現這個地址屬於他。
另一種方式是:隱身地址提供與 Bob 相同的隱私屬性,為每筆交易生成一個新地址,但不需要 Bob 的任何交互。
隱身地址方案的完整工作流程如下所示:
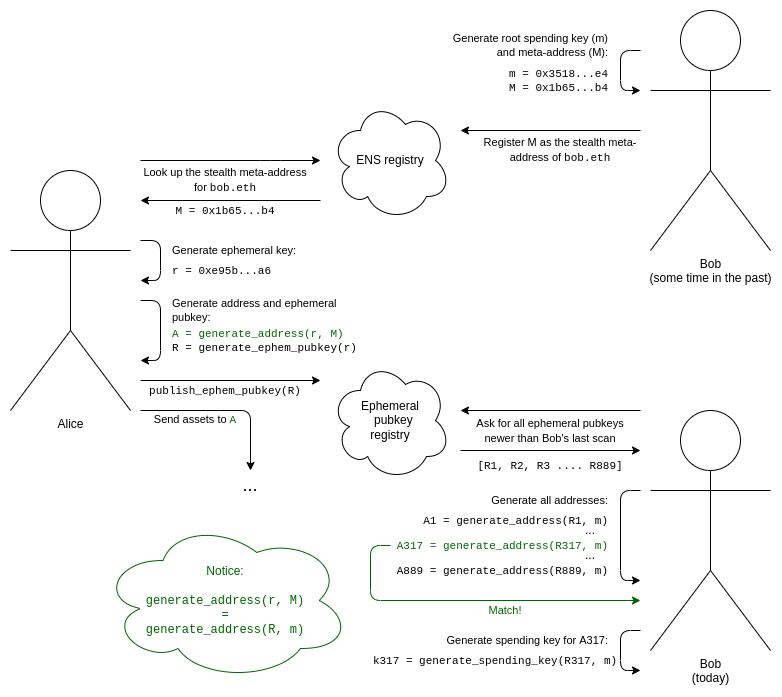
- Bob 生成他的根支出密鑰 (m) 和隱形元地址 (M)。
- Bob 添加一條 ENS 記錄以將 M 註冊為 bob.eth 的隱形元地址。
- 我們假設 Alice 知道 Bob 是 bob.eth。Alice 在 ENS 上查找他的隱身元地址 M。
- Alice 生成一個只有她知道的臨時密鑰,並且她只使用一次(生成這個特定的隱形地址)。
- Alice 使用一種算法,將她的臨時密鑰和 Bob 的元地址結合起來生成一個隱身地址。她現在可以將資產發送到這個地址。
- Alice 還生成了她的臨時公鑰,並將其發佈到臨時公鑰註冊表(這可以在與將資產發送到該隱身地址的第一筆交易相同的交易中完成)。
- 為了讓 Bob 發現屬於他的隱身地址,Bob 需要掃描臨時公鑰註冊表以查找自上次掃描以來任何人出於任何原因發布的整個臨時公鑰列表。
- 對於每個臨時公鑰,Bob 嘗試將其與他的根支出密鑰結合起來生成一個隱形地址,並檢查該地址中是否有任何資產。如果有,Bob 計算該地址的支出密鑰並記住它。
這一切都依賴於密碼欺騙的兩種用途。首先,我們需要一對算法來生成共享秘密:一個算法使用 Alice 的秘密事物(她的臨時密鑰)和 Bob 的公開事物(他的元地址),另一個算法使用 Bob 的秘密事物(他的根花費密鑰)) 和 Alice 的公開事物(她的臨時公鑰)。這可以通過多種方式完成; Diffie-Hellman 密鑰交換是建立現代密碼學領域的成果之一,它也正是實現了這一點。
但是僅共享秘密是不夠的:如果我們只是從共享秘密生成一個私鑰,那麼 Alice 和 Bob 都可以從這個地址消費。我們可以就此打住,讓 Bob 將資金轉移到新地址,但這樣做效率低下並且不必要地降低了安全性。所以我們還添加了一個密鑰盲化機制:一對算法,Bob 可以將共享秘密與他的根支出密鑰結合起來,Alice 可以將共享秘密與 Bob 的元地址結合起來,這樣 Alice 就可以生成隱身地址,並且 Bob 可以為該隱身地址生成支出密鑰,所有這些都無需在隱身地址和 Bob 的元地址之間(或一個隱身地址與另一個隱身地址之間)創建公共鏈接。
使用橢圓曲線密碼術的隱身地址
使用橢圓曲線密碼術的隱身地址最初是由 Peter Todd 於 2014 年在比特幣的背景下引入的。該技術的工作原理如下(這假定了基本橢圓曲線密碼技術的先驗知識;請參見此處、此處和此處以獲取一些教程):
- Bob 生成一個密鑰 m,併計算 M = G * m,其中 G 是橢圓曲線的共同商定生成點。隱形元地址是 M 的編碼。
- Alice 生成一個臨時密鑰 r,並發布臨時公鑰 R = G * r。
- Alice 可以計算出一個共享秘密 S = M * r,而 Bob 可以計算出相同的共享秘密 S = m * R。
- 一般來說,在比特幣和以太坊(包括正確設計的 ERC-4337 賬戶)中,地址是包含用於驗證來自該地址的交易的公鑰的哈希。因此,如果您計算公鑰,就可以計算地址。為了計算公鑰,Alice 或 Bob 可以計算 P = M + G * hash(S)
- 為了計算該地址的私鑰,Bob(和 Bob 一個人)可以計算 p = m + hash(S)
這滿足了我們上面的所有要求,而且非常簡單!
今天甚至有一個 EIP 試圖為以太坊定義一個隱身地址標準,它既支持這種方法,又為用戶提供了開發其他方法的空間(例如,支持 Bob 擁有單獨的支出和查看密鑰,或者使用不同的密碼學來實現抗量子安全)。現在你可能會想:隱身地址並不難,理論已經紮實,採用只是一個實現細節。然而,問題在於,真正有效的實施需要通過一些相當大的實施細節。
隱身地址和支付交易費用
假設有人給你發了一個 NFT。考慮到您的隱私,他們會將其發送到您控制的一個隱身地址。掃描鏈上的 ephem 公鑰後,您的錢包會自動發現該地址。您現在可以自由證明這個 NFT 的所有權或將其轉讓給其他人。但是有一個問題!該帳戶中的 ETH 為 0,因此無法支付交易費用。即使是 ERC-4337 代幣付款人也不會工作,因為它們只適用於可替代的 ERC20 代幣。而且你不能從你的主錢包向它發送 ETH,因為那樣你就創建了一個公開可見的鏈接。

插入 2017 年(或更早)加密騙局人物的模因是作家可以用來表示博學和受人尊敬的一項重要技術,因為這表明他們已經入圈很長時間並且品味高雅,並且不容易被像 SBF 這樣的人所騙。
有一種 “簡單” 的方法可以解決這個問題:只需使用 ZK-SNARKs 轉移資金來支付費用!但是這樣會消耗大量的 gas,單次轉賬就多了幾十萬 gas。
另一種聰明的方法涉及信任專門的交易聚合器(MEV 術語中的 “搜索者”)。這些聚合器將允許用戶支付一次以購買一組可用於支付鏈上交易的 “票”。當用戶需要在一個不包含任何其他內容的隱身地址中花費 NFT 時,他們會向聚合器提供其中一張票,使用 Chaumian 盲化方案進行編碼。這是在 1980 年代和 1990 年代提出的中心化隱私保護電子現金方案中使用的原始協議。搜索者接受 “票”,並重複將交易免費包含在他們的捆綁包中,直到交易在一個區塊中被成功接受。由於涉及的資金量少,而且只能用於支付交易手續費,因此信任和監管問題遠低於 “完全” 實施這種中心化隱私保護電子現金。
隱身地址和分離支出和查看密鑰
假設 Bob 不是只有一個可以做所有事情的主 “根支出密鑰”,而是想要一個單獨的根支出密鑰和查看密鑰。查看密鑰可以看到 Bob 的所有隱形地址,但不能從中花費。
在橢圓曲線世界中,這可以使用一個非常簡單的密碼技巧來解決:
- Bob 的元地址 M 現在的形式為 (K, V),編碼為 G * k 和 G * v,其中 k 是支出密鑰,v 是查看密鑰。
- 共享秘密現在是 S = V * r = v * R,其中 r 仍然是 Alice 的臨時密鑰,R 仍然是 Alice 發布的臨時公鑰。
- 隱身地址的公鑰是 P = K + G * hash(S),私鑰是 p = k + hash(S)。
請注意,第一個聰明的加密步驟(生成共享秘密)使用查看密鑰,第二個聰明的加密步驟(Alice 和 Bob 的並行算法生成隱身地址及其私鑰)使用根支出密鑰。
這有很多用例。例如,如果 Bob 想要接收 POAP,那麼 Bob 可以給他的 POAP 錢包(或者甚至是一個不太安全的 Web 界面)他的查看密鑰來掃描鏈並查看他的所有 POAP,而不需要給這個界面花費那些 POAP 的權力。
隱身地址和更容易掃描
為了更容易地掃描整個臨時公鑰集,一種技術是向每個臨時公鑰添加一個視圖標籤。在上述機制中執行此操作的一種方法是使視圖標籤成為共享秘密的一個字節(例如,S 模 256 的 x 坐標,或 hash(S) 的第一個字節)。
這樣,Bob 只需要為每個臨時公鑰執行一次橢圓曲線乘法來計算共享秘密,而 Bob 需要進行更複雜的計算以生成和檢查完整地址的時間只有 1/256。
隱身地址和抗量子安全
上面的方案依賴於橢圓曲線,它很好,但不幸的是容易受到量子計算機的攻擊。如果量子計算機成為一個問題,我們將需要切換到抗量子算法。有兩個自然的候選者:橢圓曲線同源和格(lattices)。
橢圓曲線同源是一種非常不同的基於橢圓曲線的數學構造,它具有線性特性,可以讓我們使用與上面所做的類似的密碼技巧,但巧妙地避免了構造可能容易受到量子計算機離散對數攻擊的循環群。
基於同源性的密碼學的主要弱點是其高度複雜的底層數學,以及在這種複雜性下隱藏可能的攻擊的風險。去年,一些基於同種基因的協議被攻破,但其他協議仍然安全。同源性的主要優勢是相對較小的密鑰大小,以及直接移植多種基於橢圓曲線的方法的能力。
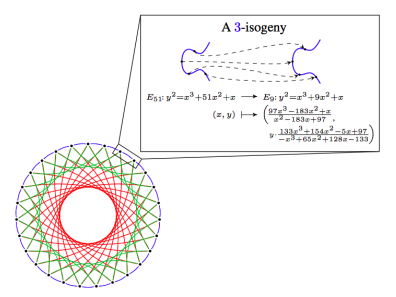
格(Lattices)是一種非常不同的密碼結構,它依賴於比橢圓曲線同構簡單得多的數學,並且能夠完成一些非常強大的事情(例如全同態加密(FHE))。隱形地址方案可以建立在格上,儘管設計最好的方案是一個懸而未決的問題。然而,基於格的結構往往具有更大的密鑰大小。
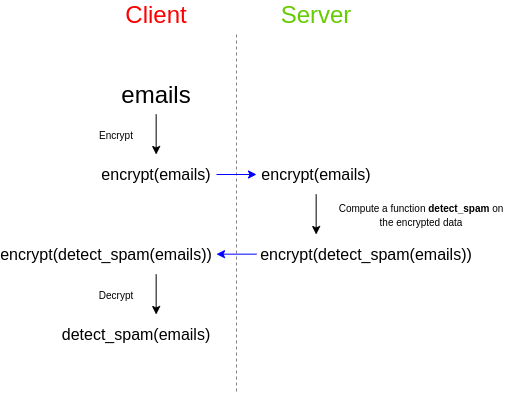
全同態加密,這是格的一種應用。FHE 還可以用於以不同的方式幫助隱形地址協議:幫助 Bob 外包檢查整個鏈中是否包含資產的隱形地址的計算,而無需透露他的視圖密鑰。
第三種方法是從通用黑盒原語構建隱身地址方案:許多人出於其他原因需要的基本成分。該方案的共享秘密生成部分直接映射到密鑰交換,這是公鑰加密系統中的一個重要組成部分。更難的部分是讓 Alice 只生成隱形地址(而不是支出密鑰)並讓 Bob 生成支出密鑰的並行算法。
不幸的是,您無法使用比構建公鑰加密系統所需的成分更簡單的成分來構建隱形地址。有一個簡單的證明:你可以用一個隱蔽的地址方案構建一個公鑰加密系統。如果 Alice 想給 Bob 加密一條消息,她可以發送 N 筆交易,每筆交易要么發往 Bob 的一個隱身地址,要么發往一個屬於她自己的隱身地址,Bob 可以看到他收到了哪些交易來讀取消息。這很重要,因為有數學證明你不能只用哈希來做公鑰加密,而你可以只用哈希來做零知識證明——因此,隱形地址不能只用哈希來完成。
這是一種確實使用相對簡單成分的方法:零知識證明,可以由哈希和(密鑰隱藏)公鑰加密組成。Bob 的元地址是一個公開的加密密鑰加上一個哈希 h = hash(x),他的支出密鑰是對應的解密密鑰加上 x。為了創建一個隱身地址,Alice 生成一個值 c,並將 Bob 可讀的 c 加密作為她的臨時公鑰發布。地址本身是一個 ERC-4337 帳戶,其代碼通過要求交易提供零知識證明來驗證交易,證明值 x 和 c 的所有權,使得 k = hash(hash(x), c)(其中 k 是賬戶代碼)。知道 x 和 c,Bob 可以自己重建地址及其代碼。
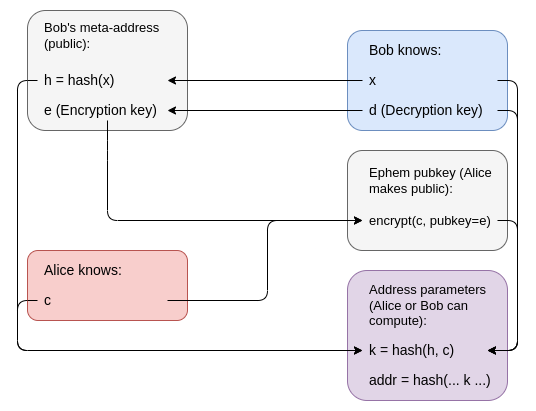
c 的加密不會告訴 Bob 任何其他人任何信息,而且 k 是一個哈希,因此它幾乎不會透露任何關於 c 的信息。錢包代碼本身只包含 k,c 是私有的,意味著 k 無法追溯到 h。
然而,這需要一個 STARK,而 STARK 很大。最終,我認為後量子以太坊世界很可能會涉及許多應用程序使用許多 Stark,因此我提倡像此處描述的聚合協議將所有這些 STARK 組合成一個遞歸 STARK 以節省空間。
隱身地址和社交恢復以及多 L2 錢包
很長一段時間以來,我一直是社交恢復錢包的粉絲:具有多重簽名機制的錢包,其密鑰在機構、您的其他設備和您的朋友之間共享,其中一些絕大多數密鑰可以恢復對您帳戶的訪問,除非您丟失主秘鑰。
然而,社交恢復錢包不能很好地與隱身地址混合:如果你必須恢復你的賬戶(意思是,改變控制它的私鑰),你還必須執行一些步驟來改變你的 N 個隱身錢包的賬戶驗證邏輯,這將需要 N 筆交易,以高昂的費用、便利性和隱私成本為代價。
社交恢復和多個第 2 層協議的世界的相互作用也存在類似的擔憂:如果你在 Optimism、Arbitrum、Starknet、Scroll、Polygon 有賬戶,並且可能其中一些 rollups 上出於擴展原因有十幾個並行實例,並且您在每個實例上都有一個帳戶,那麼更改密鑰可能是一個非常複雜的操作。

一種方法是硬著頭皮接受恢復是罕見的,而且代價高昂和痛苦是可以接受的。也許您可以使用一些自動化軟件在兩週的時間跨度內以隨機間隔將資產轉移到新的隱蔽地址,以降低基於時間的鏈接的有效性。但這遠非完美。另一種方法是在監護人之間秘密共享根密鑰,而不是使用智能合約恢復。但是,這會消除停用監護人幫助恢復您帳戶的權力的能力,因此存在長期風險。
一種更複雜的方法涉及零知識證明。考慮上面基於 ZKP 的方案,但修改邏輯如下。賬戶不是直接持有 k = hash(hash(x), c),而是持有(隱藏)鏈上 k 位置的承諾。從該賬戶支出然後需要提供一個零知識證明(i)你知道鏈上與該承諾匹配的位置,以及(ii)該位置的對象包含一些值 k(你沒有透露),並且你有一些值 x 和 c 滿足 k = hash(hash(x), c)。
這允許許多帳戶,甚至跨越許多第 2 層協議,在某處(在基礎鏈上或某些第 2 層上)由單個 k 值控制,其中更改一個值足以更改所有帳戶的所有權,所有這些都不會洩露您的帳戶之間的聯繫。
結論
基本的隱身地址今天可以相當快地實施,並且可以顯著提高以太坊上的實際用戶隱私。他們確實需要在錢包方面做一些工作來支持他們。也就是說,我認為出於其他與隱私相關的原因,錢包應該開始轉向更原生的多地址模型(例如,為您與之交互的每個應用程序創建一個新地址可能是一種選擇)。
然而,隱身地址確實會帶來一些長期的可用性問題,例如社交恢復的困難。現在可以簡單地接受這些擔憂,例如。通過接受社交恢復將涉及隱私的喪失或延遲兩週以緩慢地將恢復交易發佈到各種資產(這可以由第三方服務處理)。從長遠來看,這些問題是可以解決的,但從長遠來看,隱身地址生態系統看起來確實嚴重依賴於零知識證明。
免責聲明:作為區塊鏈信息平台,本站所發布文章僅代表作者及嘉賓個人觀點,與 Web3Caff 立場無關。文章內的信息僅供參考,均不構成任何投資建議及要約,並請您遵守所在國家或地區的相關法律法規。