本文旨在解釋交易所可償付證明的基本原理,並進一步探討資產託管光譜兩端 CEX 和 DEX 中間的更多可能性。
原文:Having a safe CEX: proof of solvency and beyond(vitalik.ca)
翻譯:雙花 (@doublespending)
審閱: ECN
封面: Photo by Pawel Czerwinski on Unsplash
特別感謝 Balaji Srinivasan 以及 Coinbase、Kraken 和 Binance 團隊的探討。
每當大型中心化交易所崩潰時,一個常被提及的問題是:我們是否可以利用加密技術來解決這個問題。交易所可以通過創建密碼學證明的方式證明其鏈上持有的資金足以償付用戶,而不僅僅依靠政府牌照、審計員、調查公司治理以及交易所法人背調等 “法幣” 方案。
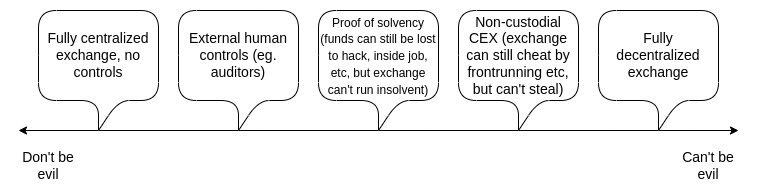
更有野心的是,交易所可以建立一個未經儲戶同意無法提取儲戶資金的系統。我們可以嘗試探索 “不作惡” 有職業素養的 CEX 與 “無法作惡” 卻洩漏隱私的低效鏈上 DEX 之間的界限。這篇文章將深入探討讓 CEX 更加去信任的歷史嘗試,與其採用技術的局限性,以及一些依賴 ZK-SNARKs 等先進技術的有力手段。
餘額表和 Merkle 樹:傳統的可償付證明
交易所試圖用密碼學來證明自己沒有欺騙用戶的最早嘗試可以追溯到很久以前。2011 年,當時最大的比特幣交易所 MtGox 通過發送一筆移動 424,242 個 BTC 到預先公佈地址的交易來證明他們擁有該筆資金。2013 年,大家開始討論如何解決該問題的另一面:證明用戶存款的總規模。如果你證明用戶的存款等於 X(負債證明 proof of liabilities),並證明擁有 X 個代幣的私鑰(資產證明 proof of assets),那麼就提供了可償付證明(proof of solvency):你證明了交易所有足夠的資金償還給儲戶。
提供存款證明的最簡單方法是公佈一個列表。每個用戶都可以檢查他們在列表中的餘額,而且任何人都可以檢查完整的列表:(i)每項餘額都是非負的;(ii)總額是宣稱的金額。
當然,這會破壞隱私,所以我們可以稍微改變一下該方案:發布一個列表,並私下給用戶發送 salt 值。但即使這樣也會洩漏餘額與其分佈。為了保護隱私,我們採用了後續技術:Merkle 樹技術。
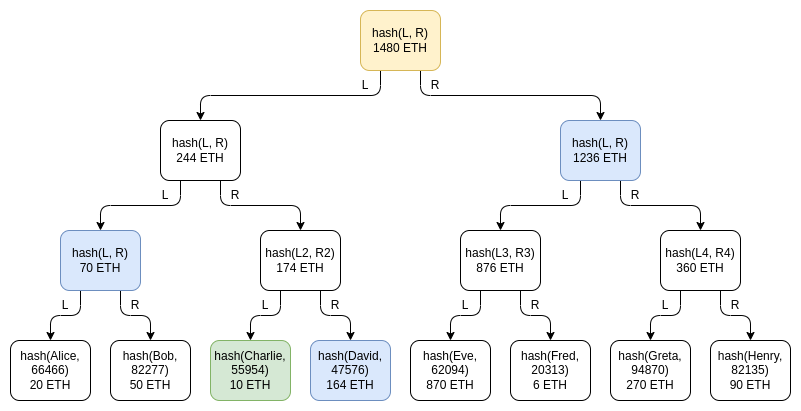
綠色:Charlie 的節點。藍色:Charlie 收到用於證明的節點。黃色:根節點,向所有人公佈
Merkle 樹技術會將用戶餘額表放進 Merkle 總和樹。在 Merkle 總和樹中,每個節點都是對。底層葉子節點表示各個用戶的餘額以及用戶名的加鹽哈希。在每個更高層的節點中,餘額是下面兩個節點餘額的總和,而哈希是下面兩個節點的哈希。Merkle 總和證明和 Merkle 證明一樣,是一個由葉子節點到根節點路徑上所有姐妹節點組成的 “分支”。
首先,交易所會向每個用戶發送一份其餘額的 Merkle 總和證明。然後,用戶能夠確定其餘額作為總額的一部分而被正確地包含。可以在這裡找到簡單的示例代碼。
# The function for computing a parent node given two child nodes
def combine_tree_nodes(L, R):
L_hash, L_balance = L
R_hash, R_balance = R
assert L_balance >= 0 and R_balance >= 0
new_node_hash = hash(
L_hash + L_balance.to_bytes(32, 'big') +
R_hash + R_balance.to_bytes(32, 'big')
)
return (new_node_hash, L_balance + R_balance)
# Builds a full Merkle tree. Stored in flattened form where
# node i is the parent of nodes 2i and 2i+1
def build_merkle_sum_tree(user_table: "List[(username, salt, balance)]"):
tree_size = get_next_power_of_2(len(user_table))
tree = (
[None] * tree_size +
[userdata_to_leaf(*user) for user in user_table] +
[EMPTY_LEAF for _ in range(tree_size - len(user_table))]
)
for i in range(tree_size - 1, 0, -1):
tree[i] = combine_tree_nodes(tree[i*2], tree[i*2+1])
return tree
# Root of a tree is stored at index 1 in the flattened form
def get_root(tree):
return tree[1]
# Gets a proof for a node at a particular index
def get_proof(tree, index):
branch_length = log2(len(tree)) - 1
# ^ = bitwise xor, x ^ 1 = sister node of x
index_in_tree = index + len(tree) // 2
return [tree[(index_in_tree // 2**i) ^ 1] for i in range(branch_length)]
# Verifies a proof (duh)
def verify_proof(username, salt, balance, index, user_table_size, root, proof):
leaf = userdata_to_leaf(username, salt, balance)
branch_length = log2(get_next_power_of_2(user_table_size)) - 1
for i in range(branch_length):
if index & (2**i):
leaf = combine_tree_nodes(proof[i], leaf)
else:
leaf = combine_tree_nodes(leaf, proof[i])
return leaf == root這種設計下的隱私洩露遠低於公開完整的餘額表,並可以在每次默克爾根發佈時打亂各個分支來進一步降低隱私洩漏風險,但仍存在一些隱私洩露的問題:Charlie 知道某人的餘額為 164 ETH,某兩個用戶餘額的總和為 70 ETH,等等。控制多個帳戶的攻擊者仍能了解交易所用戶的大量信息。
該方案的一個重要的微妙之處在於負餘額的可能性:如果一個擁有 1390 ETH 用戶餘額卻只有 890 ETH 儲備的交易所試圖通過在樹上某處的一個假賬戶下添加-500 ETH 餘額來彌補差額,該怎麼辦?這種可能性實際上並沒有破壞該方案,這就是我們特地使用 Merkle 總和樹而不是常規 Merkle 樹的原因。假設 Henry 是交易所控制的假賬戶,而且交易所在上面放了-500 ETH:
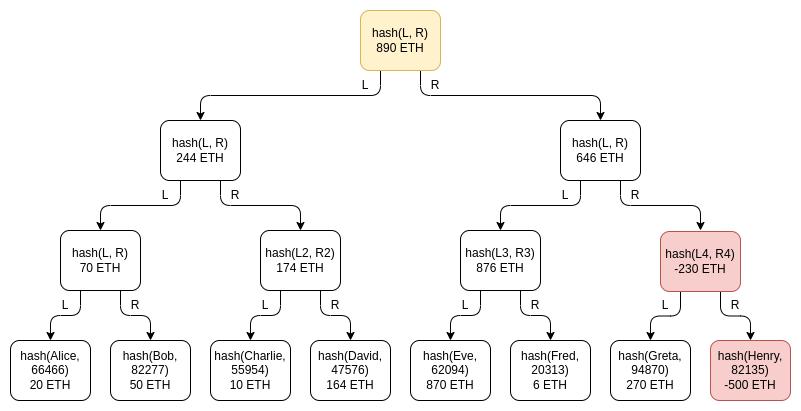
Greta 的驗證將不會通過:當交易所將不得不把 Henry 餘額為-500 ETH 的節點的給她時,她會拒絕掉該無效節點。Eve 和 Fred 也會驗證失敗,因為 Henry 之上的中間節點餘額為-230 ETH,所以該節點也是無效的!為了盜用行為不被發現,交易所只能寄望於樹的右半部分沒人檢查其餘額證明。
如果交易所能夠挑選出這樣的擁有 500 ETH 的用戶:他們嫌麻煩不去檢查餘額證明,或者當他們抱怨未能收到餘額證明時,大家並不相信他們,那麼交易所就可以蒙混過關。但是,交易所也可以通過將這些用戶排除在 Merkle 總和樹之外來達到相同的效果。因此,如果僅就負債證明而言,Merkle 樹技術基本滿足了需求。但它的隱私特性仍不夠理想。你可以更巧妙地使用 Merkle 樹進行改進,比如把 satoshi 或 wei 作為一個獨立的葉子節點。然而,通過使用更先進的技術,還可以做得更好。
使用 ZK-SNARKs 來提高隱私性和健壯性
ZK-SNARKs 是一項強大的技術。ZK-SNARKs 對密碼學的意義類似於人工智能:一項足以碾壓數十年前為了解決一系列問題而開發的一系列專用技術的通用技術。因此,我們當然可以使用 ZK-SNARKs 極大地簡化和改善負債證明協議中的隱私。
我們可以簡單地將所有用戶的存款放進 Merkle 樹(或者更為簡單的 KZG 承諾),並使用 ZK-SNARK 來證明樹中的所有餘額都是非負的,並且加起來等於某個聲稱的值。如果我們添加了一層哈希來保證隱私,那麼發給每個用戶的 Merkle 分支(或 KZG 證明)將不會洩漏任何其他用戶的餘額。
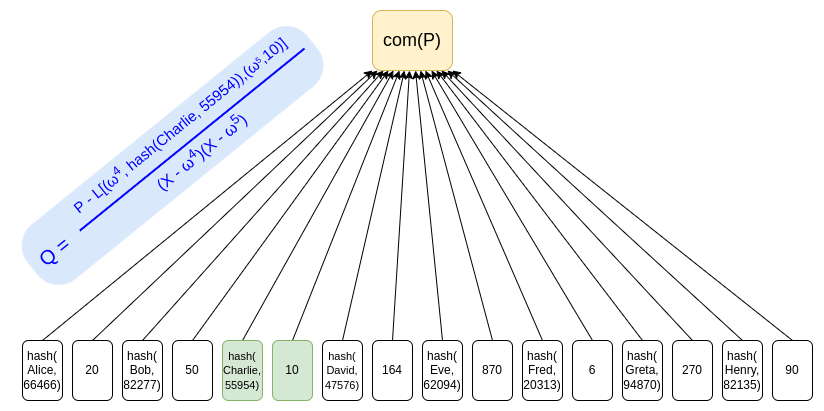
使用 KZG 承諾是避免隱私洩露的一種方法,因為其不需要把 “姐妹節點” 作為證明提供,並且可以使用簡單的 ZK-SNARK 來證明餘額的總和,並且每個餘額都是非負的。
我們可以通過一個專用的 ZK-SNARK 來證明上述 KZG 中餘額的總和及其非負性。這裡有一個簡單的例子。我們引入了一個輔助多項式 I(x),其 “構建出用戶餘額的每一位”(為了舉例,我們假設餘額低於 215),其中每第 16 個位置追踪差額保證,只有當實際總額與宣稱總額相等該值才會是 0。如果 z 是一個 128 階的原根,我們可以證明方程成立:

如何把這些等式轉換為多項式校並在後續轉換為 ZK-SNARK 可以參考我撰寫關於 ZK-SNARKs 文章的此處和另外一處。這並不是一個最優的協議,但讓這些密碼學證明比較好理解!
只需要幾個額外的方程式,該約束系統就可以適配更複雜的設定。例如,在槓桿交易系統中,個人用戶擁有負餘額是可以接受的,但前提是他們需要擁有足夠的抵押資產以覆蓋其負債。SNARK 可以用於證明這一更為複雜的約束,向用戶保證,交易所不能秘密違規豁免某些用戶,從而危及用戶資產。
長遠來看,這種 ZK 負債證明的用處不限於交易所中的用戶存款,還可以用於更廣泛的貸款場景。任何貸款的人都會將記錄放入含該貸款的一個多項式或一棵樹中,而根會在鏈上發布。這將使得任何尋求貸款的人向放款方提供零知識證明,以表明其未獲得太多其他貸款。最終,法律上的創新甚至可以使得以這種方式進行承諾的貸款比無承諾的貸款擁有更高的優先級。這與我們在《去中心化社會:尋找 Web3 的靈魂》中討論的一個想法不謀而合:通過某種形式的” 靈魂綁定代幣 “,使得鏈上負面信譽的概念成為可能。
資產證明
資產證明最簡單的版本是我們上面看到的協議:為了證明您持有 X 個代幣,您只需在預定時間移動 X 個代幣或在交易中攜帶 “這些資金屬於 Binance” 的信息。為了避免支付交易手續費,你可以簽署一條鏈下消息。比特幣和以太坊都有鏈下簽名信息標準。
這種簡單的資產證明技術存在兩個實際問題:
● 冷錢包處理
● 抵押品重用
出於安全考慮,大多數交易所會將大部分用戶資金存儲在冷錢包中:在離線的計算機上,交易需要手動簽名並攜帶到互聯網上。這種手段是很普遍的:我過去用於存放私人資金的冷錢包放在一台永久離線的計算機上,它會生成包含已簽名交易的二維碼,然後我會用手機掃描這些二維碼。由於資金量龐大,交易所使用的安全協議會更加複雜,經常涉及在多個設備間的多方計算,以進一步降低單設備被黑導緻密鑰洩露的可能性。在這種背景下,即使是創建一條額外消息來證明對地址的控制也是一項昂貴的操作!
交易所可以採用以下幾種方式:
● 維護一些長期使用的公開地址。交易所生成若干地址,僅發布一次每個地址所有權證明,然後重複使用這些地址。這是迄今為止最簡單的方案,儘管它在保護安全及隱私上增加了一些限制。
● 持有很多地址,然後隨機證明幾個地址。交易所持有很多地址,甚至可能每個地址只用一次,並在單次交易後不再使用。在這種情況下,交易所需要有一個協議,不時地隨機選擇一些地址,交易所必須 “打開” 以證明所有權。一些交易所已通過審計員進行了類似的操作,但原則上,這種技術可以轉化為完全自動化的程序。
● 更複雜的 ZKP 方式。例如,交易所可以將其所有地址設置 1/2 多簽,這些地址的其中一份密鑰各不相同,而另一份相同的密鑰是以某種複雜但安全的方式(如,12/16 多簽)存儲起來重要的緊急備份盲版。為了保護隱私並避免洩漏其全部地址,交易所甚至可以在區塊鏈上運行零知識證明以證明該格式鏈上地址的總餘額。
另一個主要問題是防止抵押品重用。彼此間來迴轉移抵押品以證明儲備金對交易所而言通常很容易辦到,這使得實際上沒有償付能力的情況下蒙混過關。理想情況下,可償付證明應該實時完成,並在每個區塊後更新證明。如果不切實際的話,那麼下一個最好的辦法就是交易所間協調出一個固定的時間進行證明,例如在 UTC 時間每週二下午 2 點證明儲備。
最後一個問題是:能在法定貨幣上做資產證明嗎?交易所不僅持有加密貨幣,還持有銀行系統內的法幣。在這方面,回答是肯定的,但這樣的程序將不可避免地依賴於 “法幣” 信任模型:銀行自身可以證明餘額,審計人員可以證明資產負債表等。鑑於法幣不能通過密碼學驗證,這是在該框架內的最佳方案,仍然值得一做。
另一種方法是將實體 A 和實體 B 分離開來,A 負責運行交易所並且處理 USDC 這種由某種資產背書的穩定幣;而 B 負責在加密貨幣和傳統銀行系統之間處理現金流入和流出的過程,在這個案例中 B 即是 USDC 本身。由於 USDC 的 “負債” 只是鏈上的 ERC20 代幣,所以負債證明是可以 “輕易” 獲得的,而我們只需處理資產證明的問題。
Plasma 和 validiums: 我們可以實現非託管 CEX 嗎?
假設我們想更進一步:我們不想僅僅證明交易所有足夠資金償還其用戶。相反,我們想徹底防止交易盜用用戶的資金。
在這上第一個嚐鮮的是 Plasma,這是一種 2017 年和 2018 年在以太坊研究界流行的擴容解決方案。Plasma 的工作原理是將餘額拆分為一組獨立的 “代幣”,每個代幣都會分配一個索引,並放到 Plasma 區塊的 Merkle 樹中的特定位置上。要進行有效的代幣轉移,需要將交易放到樹中的正確位置上,而樹根會被發佈到鏈上。
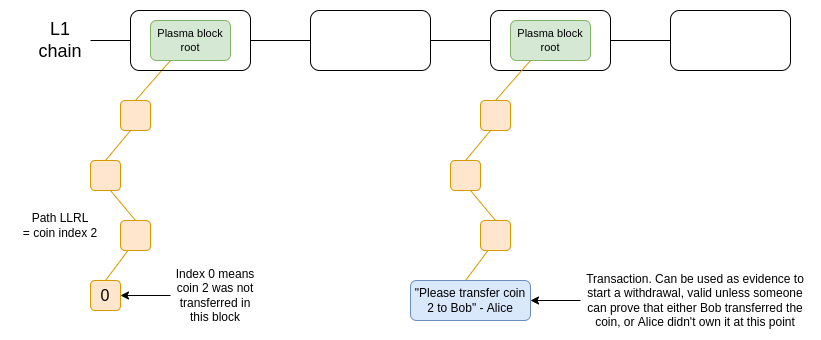
Plasma 的一個版本的極簡圖。代幣被保存在智能合約中,該合約在取款時會強制執行 Plasma 協議的規則。
OmiseGo 試圖基於此協議創建一個去中心化交易所,但從那時起,他們就轉向去做其他事了——就這而言,Plasma Group 也是如此,他們去做了 optimistic rollup 項目 Optimism。
2018 年對 Plasma 的局限性(如,證明代幣碎片整理)的探討讓大家從根本上懷疑 Plasma 的可行性。自 2018 年對 Plasma 的探討達到頂峰以來,ZK-SNARKs 在擴容相關用例上變得愈加可行,正如我們上面所說的,ZK-SNARKs 改變了一切。
Plasma 更新的版本是 Starkware 稱為 validium 的方案:除了數據被保存在鏈下以外,基本上與 ZK-rollup 相同。該構造適用於許多用例,可以想像其適用於任何中心化服務器需要證明其正確執行代碼的場景。在 validium 中,運營方無法竊取資金,但根據具體的實現細節,如果運營方消失,一些用戶資金可能會被卡住。
現在看來一切很棒:CEX 和 DEX 遠非二選一,事實證明,其中有一系列的選擇,包含各種形式的混合中心化,在那裡你能獲得一些好處,比如效率,但仍有很多密碼學保障,可以防止中心化運營方的大部分形式的惡意行為。
然而,餘下的基本問題也值得思考:如何處理用戶錯誤。到目前為止,最重要的錯誤類型是:如果用戶忘記了密碼、丟失了設備、被黑或無法訪問其帳戶,那該怎麼辦?
交易所可以解決這個問題:首先利用電子郵件恢復,如果連這都失敗了,再通過 KYC 進行更複雜的恢復。但若要解決這些問題,交易所需要真正控制這些代幣。為了能夠合理地恢復用戶資金,交易所需要擁有同樣可用於無故竊取用戶資金的權力。這是一個不可避免的權衡。
理想的長期解決方案是依靠自我託管,用戶在未來可以方便地使用諸如多簽及社交恢復錢包等技術來幫助處理緊急情況。而短期內,有兩種明顯的替代方案,有著不同的成本和收益:

另一個重要問題是對跨鏈支持:交易所需要支持很多不同的鏈,諸如 Plasma 和 validiums 等系統需要用不同的語言編寫代碼以支持不同的平台,並且在當前形式下無法在一些平台(尤其是比特幣)上實現,這有望通過技術升級和標準化來解決;然而,從短期來看,這是如今託管型交易所保持託管模式的另一個原因。
結論:展望未來更好的交易所
短期內,有兩種明確的交易所類別:託管型交易所和非託管型交易所。如今,後一類即像 Uniswap 那樣的 DEX,未來我們可能還會看到受密碼學約束的 CEX,其中用戶資金會以類似 validium 智能合約的方式持有。我們也可能會看到半託管型交易所,其中我們信任其對法幣而非加密貨幣的處理。
這兩種類型的交易所將繼續存在,而提高託管型交易所安全性的向後兼容最簡單方法是增加儲備證明。這包括資產證明和負債證明的結合。為兩者都設計出優秀的協議仍存在著一些挑戰,但我們能夠且應當推動兩類技術的齊頭並進,並儘可能開源軟件和程序,以便所有交易所都能獲益。
從長遠來看,我希望我們向著所有交易所皆為非託管的方向發展,至少在加密貨幣上如此。錢包恢復將會存在,可能需要為小額資金的新用戶和出於法律因素需要此類安排的機構提供高度中心化的恢復選項,但這可以在錢包層而非交易所內部完成。在法幣方面,傳統銀行系統和加密貨幣生態系統之間的移動可以通過 USDC 等資產背書穩定幣原生的資金進出流程完成。然而,我們仍有很長的路要走。[1] 譯者註:
➤ 每 16 個數字代表一個用戶(前面 15 個數字代表該用戶的餘額,最後一位代表目前為止用戶餘額總和跟聲明的差額)。我們可以看到上面的舉例代表了兩個用戶(這裡要讀者洞察一下)
➤ 宣稱的用戶平均餘額:185
➤ 用戶 1 的餘額:20 -> 000 0000 0001 0100
差額:20 – 185 = -165
➤ 用戶 2 的餘額:50 -> 000 0101 0011 0010
差額:-165 + 50 -185 = -300
➤ 最終遍歷完所有用戶,最後一個用戶的差額要求為 0
➤ 四個等式的解釋
等式 1:遞推的初始值為 0
等式 2:每個用戶餘額需要跟 KZG commitment 相對應
等式 3:每個用戶餘額的遞推公式,約束餘額>= 0 且< 214
(上面說餘額< 215 應該是筆誤,因為按照等式 3,遞推公式只有 14 個取值,I(zi) < 214,
16 個數字對應:I(z{16x})=0| I(z{16x+1}) | I(z{16x+2}) | … | I(z{16x+14}) | 差值
16 個數字對應最大取值:0 | 21 -1| 22 -1 | … | 214 -1| 差值)
等式 4:約束所有用戶總餘額與交易所宣稱的餘額一致
特別感謝 ECN 社區翻譯志願者 @doublespending 對本文的翻譯貢獻。
免責聲明:作為區塊鏈信息平台,本站所發布文章僅代表作者及嘉賓個人觀點,與 Web3Caff 立場無關。文章內的信息僅供參考,均不構成任何投資建議及要約,並請您遵守所在國家或地區的相關法律法規。













