本文將深入探討 Google 量子晶片「Willow」對區塊鏈安全可能產生怎樣的影響。
作者: Max He,Safeheron team
谷歌最新量子運算晶片「Willow」的推出在全球科技界引發了廣泛關注。這項突破性進展不僅展示了量子計算領域的最新成果,也引發了人們對其可能影響區塊鏈技術安全性的深入討論。區塊鏈技術的安全基礎建立在複雜的密碼學難題之上,而量子運算的發展可能會對這項基礎構成挑戰。本文將深入探討 Google 量子晶片「Willow」對區塊鏈安全可能產生怎樣的影響。
初窺量子晶片 “Willow”
根據官方消息【1】,Google 發布了最新的量子運算晶片「Willow」,宣布取得了兩項重大突破。

然而,事情的真相真的是這樣嗎?讓我們進一步探討這個問題。
破解區塊鏈私鑰需要什麼樣的量子電腦?
量子電腦可以用來破解大整數分解問題和離散對數難題等經典密碼學難題。可是對於具體的密碼學問題,需要怎樣性能的量子電腦來破解呢?接下來我們用以下問題來具體分析:
- 給定 RSA2048 的公鑰,對其進行大整數分解;
- 給定一個橢圓曲線 Secp256k1/ Secp256r1 / Ed25519 的公鑰,計算其私鑰。
對於經典計算機而言,以上兩個問題都難以破解。考慮到特定安全參數,後者略難於前者。然而,Martin 等人的研究【3】揭示,對量子電腦來說,情況恰恰相反:前者略難於後者。為簡化討論,本文將這兩個問題視為近似難度,認為破解它們的量子電腦效能基本上等同。以下分析將以問題 2 為主。
Secp256k1、Secp256r1 和 Ed25519 是區塊鏈廣泛採用的橢圓曲線,這些橢圓曲線上的離散對數問題構成了包括比特幣在內所有區塊鏈資產安全的基石。若該問題被攻破,意味著攻擊者可以隨意偽造區塊鏈上的交易。顯然,此問題的破解與否直接關乎區塊鏈安全的生存。
Martin 等人的研究【3】指出,要破解定義在素數階(階的位寬為 n 位元)橢圓曲線上的離散對數難題,需要這樣的量子電腦: 9n+2⌈log2(n)⌉+ 10 個量子位元,並使用 448n3log2(n)+4090n3 個 Toffoli 閘的量子電路實現。例如,對於 NIST 標準化曲線 P-256 的點加法量子電路模擬,實現需要 2330 個邏輯量子位元,而在此曲線上完整實現 Shor 演算法在約需 1.26⋅1011 個 Toffoli 閘。
簡而言之,只需 2330 個高品質的邏輯量子位元和 1.26⋅1011 個 Toffoli 閘組成的量子電路,這樣的量子電腦就足以摧毀區塊鏈安全的根基。
量子運算的關鍵—高品質的邏輯量子比特
基於量子晶片的量子計算機之所以計算速度遠超經典計算機,其核心優勢在於量子計算不再依賴線性計算方式,而是利用量子疊加和量子並行性,透過量子位元(qubits)實現複雜計算。然而,量子比特的獨特性同時帶來了極大的挑戰。量子位元極易受到環境雜訊和外界幹擾的影響,這使得它們的狀態非常不穩定,容易失去量子特性(即退相干)。在實際操作中,幾乎每個使用量子位元的環節都可能出現錯誤,包括初始化、狀態維持、量子閘操作執行以及結果讀取。這些錯誤會導致量子演算法產生錯誤的結果或失去有效性,因此,保持量子比特的穩定性和正確性,獲得高品質的量子位元,成為量子電腦發展的核心挑戰之一。
为应对这一挑战,一个关键方法是构造逻辑量子比特以降低错误率。逻辑量子比特由多个物理量子比特组合而成,通过量子纠错码(如表面码、笛卡尔码)实现错误检测和修复,从而提高系统的鲁棒性和可靠性。实际上,每个逻辑比特通常需要数十到数千个物理比特来支持。尽管逻辑量子比特的实现显著提高了量子计算机的容错能力,但代价是需要大量的物理比特和复杂的纠错算法。

那麼,沒有高品質的邏輯量子比特,就無法建構實用的量子電腦。
再看量子晶片 “Willow”
現在我們已經掌握了足夠的背景知識,讓我們重新審視「Willow」的成果。
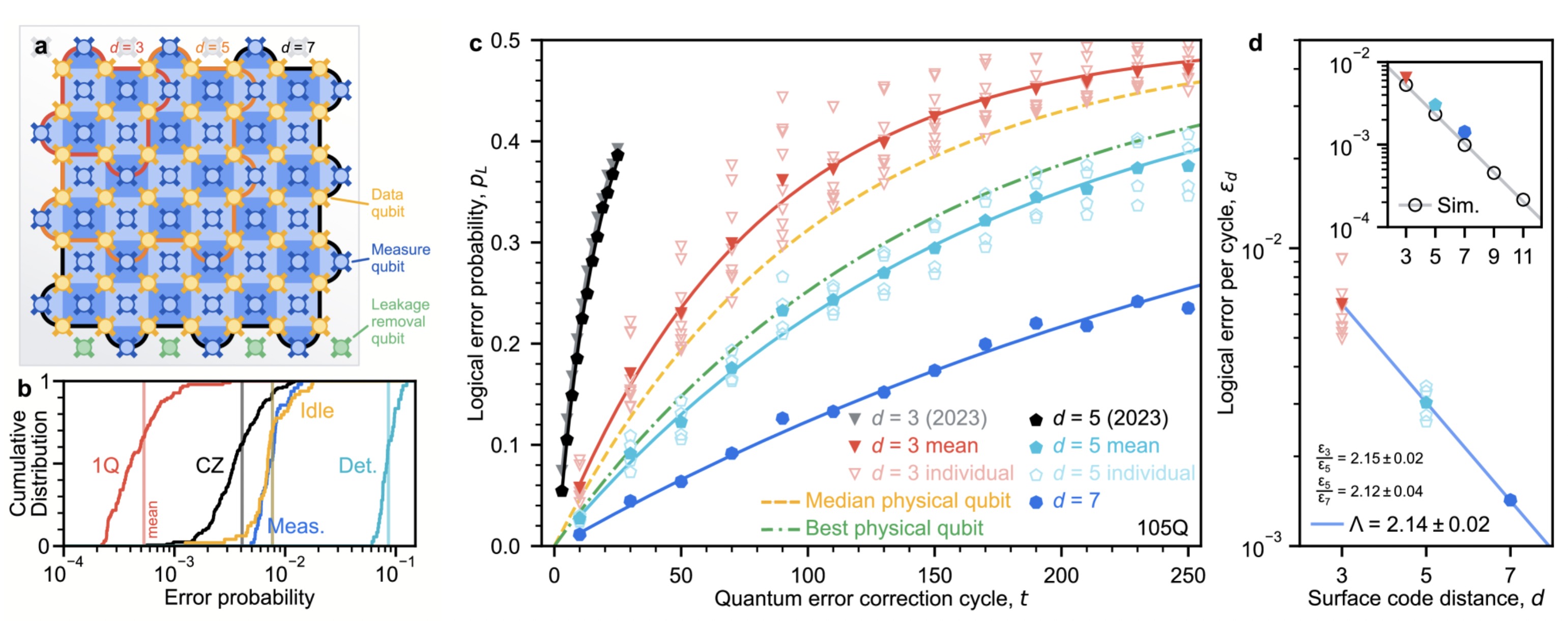
首先,「Willow」晶片透過增加量子位元數量,運用表面碼【4】【5】技術,在量子糾錯領域實現了歷史性的「扭虧為盈」。這意味著,透過投入多個實體量子位元,研究人員成功獲得了一個錯誤率更低的邏輯量子位元。具體而言,在「Willow」中,隨著量子位元陣列從 3×3 的表面碼擴展到 5×5、7×7,編碼錯誤率每次降低了 2.14 倍,實現了誤差率的指數級下降,如下圖所示。這項突破性進展首次讓人類在建構高品質邏輯量子位元的道路上看到了希望之光,堪稱一項重大成就。
其次,「Willow」晶片在不到五分鐘內完成了隨機電路取樣(Random Circuit Sampling,簡稱 RCS)這項標準基準計算。 RCS 測試是一種廣泛用於評估量子電腦效能的方法。然而,需要特別指出的是,這項測試中與超級電腦之間令人驚嘆的效能差距,部分源自於量子電腦和經典電腦的差異。為了更好地理解這一點,我們可以做一個不完全恰當的類比:「太空中的衛星」和「地面上的汽車」在比較運動速度。此外,RCS 目前也還沒有實際的應用情境。
「Willow」何時能夠攻破經典密碼學難題?

上圖為 Google 量子計算發展藍圖的六個階段【7】,展示了從實驗突破到大規模實用化的關鍵路徑。


就如本文前面所述,目前,破解區塊鏈中常見的橢圓曲線離散對數問題需要約 2330 個高品質邏輯量子位元和 1.26⋅1011 個 Toffoli 閘組成的量子電路。由於邏輯量子位元需透過量子糾錯技術實現,每個邏輯量子位元通常需要多個實體量子位元支撐。以「Willow」晶片為例,其編碼距離為 7,每個邏輯量子位元需 72=49 個實體量子位元,總計約 114170 個物理位元。然而,這項估算過於樂觀。隨著量子運算規模和電路深度的增加,邏輯量子位元的錯誤率要求將更加苛刻。實際上,「Willow」晶片目前的邏輯量子位元錯誤率約為 10−3,遠未達到破解此類問題所需的水平。根據 Craig 等人【6】的研究,為解決與橢圓曲線離散對數問題難度相近的 RSA 2048 問題,邏輯量子位元的錯誤率需降至 10−15,對應碼距至少需 27。這意味著每個邏輯量子位元需 272=729 個實體量子位元支持,總計超過 1698570 個實體量子位元。此外,邏輯量子位元錯誤率需達到 10−15,不僅顯著低於「Willow」晶片的 10−3,甚至比 Google 規劃藍圖第六階段量子電腦預期的邏輯量子位元錯誤率還低兩個數量級。
综上所述,根据谷歌的发展规划,只有在量子计算技术发展到第六阶段后,才可能具备破解椭圆曲线离散对数问题的能力。这一目标的实现需要显著提升逻辑量子比特的质量,同时解决海量物理量子比特的高效操控和纠错问题。
若以第一階段與第二階段間隔 5 年來估算,勻速發展下,預計需 15 至 20 年後,「Willow」的能力方能攻破經典密碼學難題。即便樂觀估計,至少也需 10 年才可能達到對應水準。
未來的區塊鏈安全
量子電腦一旦達到足夠的運算能力,就能利用不對稱優勢,快速破解加密貨幣的核心安全機制,竊取使用者私鑰並控制其資產。在這種情況下,現有加密貨幣網路將面臨系統性崩潰的風險,用戶資產的安全將無法得到保障。
而且,Google 的「Willow」量子晶片目前仍處於量子運算研究的初期階段,無法解決大整數分解和橢圓曲線離散對數等密碼學難題,因此尚不對區塊鏈安全構成實質威脅。事實上,開發出真正實用的量子電腦仍面臨許多技術挑戰,這注定是一條需要長期努力的艱鉅道路。
儘管目前量子運算技術尚未對加密資產構成直接威脅,但其發展勢頭不容忽視。根據技術進步趨勢預測,未來 10 年內,量子電腦可望突破多個關鍵技術瓶頸,逐步接近威脅傳統密碼學的臨界點。面對這項潛在挑戰,區塊鏈社群需要未雨綢繆,制定長遠規劃,為應對量子時代可能帶來的技術衝擊做好準備。為確保區塊鏈的長期安全性和穩定性,以下三項措施特別重要:
第一,加速抗量子演算法的研究與標準化。積極推進基於抗量子密碼學(如格理論)的演算法研究,並致力於促進其在全球範圍內的標準化應用。這是應對量子威脅的首要任務,對於未來區塊鏈安全至關重要。
第二,積極部署抗量子密碼學技術。著手建立健全的抗量子密碼基礎設施,為區塊鏈網路的長期安全奠定堅實的技術基石。這將確保系統在面對潛在的量子威脅時能夠從容應對,並保持穩定運作。
第三,深入探索量子運算的創新潛力。挖掘量子運算在鏈上運算優化、資源調度效率提升和隱私保護增強等領域的應用價值,為區塊鏈技術注入新的成長動力。
量子電腦的全面應用雖然尚未實現,但其到來已是大勢所趨。在這一背景下,基於傳統密碼學的區塊鏈安全框架將逐漸被基於抗量子密碼學的安全性所取代。Safeheron 已經與大學展開合作,積極佈局抗量子演算法研究,為數位資產安全的技術演進做好充分準備。另外,區塊鏈生態中已經出現了引入抗量子攻擊演算法的公鏈,這種與時俱進的發展趨勢讓我們無需過度憂慮。
量子運算的發展不僅為區塊鏈技術帶來了潛在的安全挑戰,也為其提供了技術進步與效率提升的新機會。只有主動應對、擁抱變革,區塊鏈技術才能在未來的科技浪潮中蓬勃發展,實現更高水準的成熟與創新。
參考文獻
【1】Meet Willow, our state-of-the-art quantum chip
【2】John Preskill – Introduction to Quantum Information (Part 1) – CSSQI 2012
【3】Quantum Resource Estimates for Computing Elliptic Curve Discrete Logarithms
【4】Suppressing quantum errors by scaling a surface code logical qubit
【5】Quantum error correction below the surface code threshold
【6】How to factor 2048 bit RSA integers in 8 hours using 20 million noisy qubits
【7】Google’s quantum computing roadmap
免責聲明:作為區塊鏈資訊平台,本站所發布文章僅代表作者及來賓個人觀點,與 Web3Caff 立場無關。文章內的資訊僅供參考,均不構成任何投資建議及要約,並請您遵守所在國家或地區的相關法律法規。