从简单和实用出发,一文读懂零知识证明
— 导读 / 原用标题
作者:BenLaw
你之前是否阅读过一些零知识证明的文章,但仍一头雾水?这些文章可能:
- 只以故事和童话作例子来论述 ZKP,无法深入其本质。
- 内含大量密码学术语,数学公式,学术论文等,对初学者而言过于复杂。
本文提供了对 ZKP 简明扼要的概述,并从数学、密码学和编程角度进一步阐述 ZKP 的核心要素。
向色盲提供颜色证明
如何向色盲患者证明两个球的颜色确实是不同的?这其实并不复杂:
让他在手里握住两个球,背到背后,然后随机选择交换或不交换两个球的位置,再展示给你看,你告诉他这两个球的位置是否有变化。
在他看来,你可以通过瞎蒙来完成一次证明。不过,如果成千上万次地重复这个过程:如果你总是能说出正确答案,那么靠纯蒙的方式来保持一直正确的概率,是小到可以忽略的。因此可以通过这种方式来向色盲患者证明:两个球的颜色确实不一样,并且我们也有感知和区分的能力。
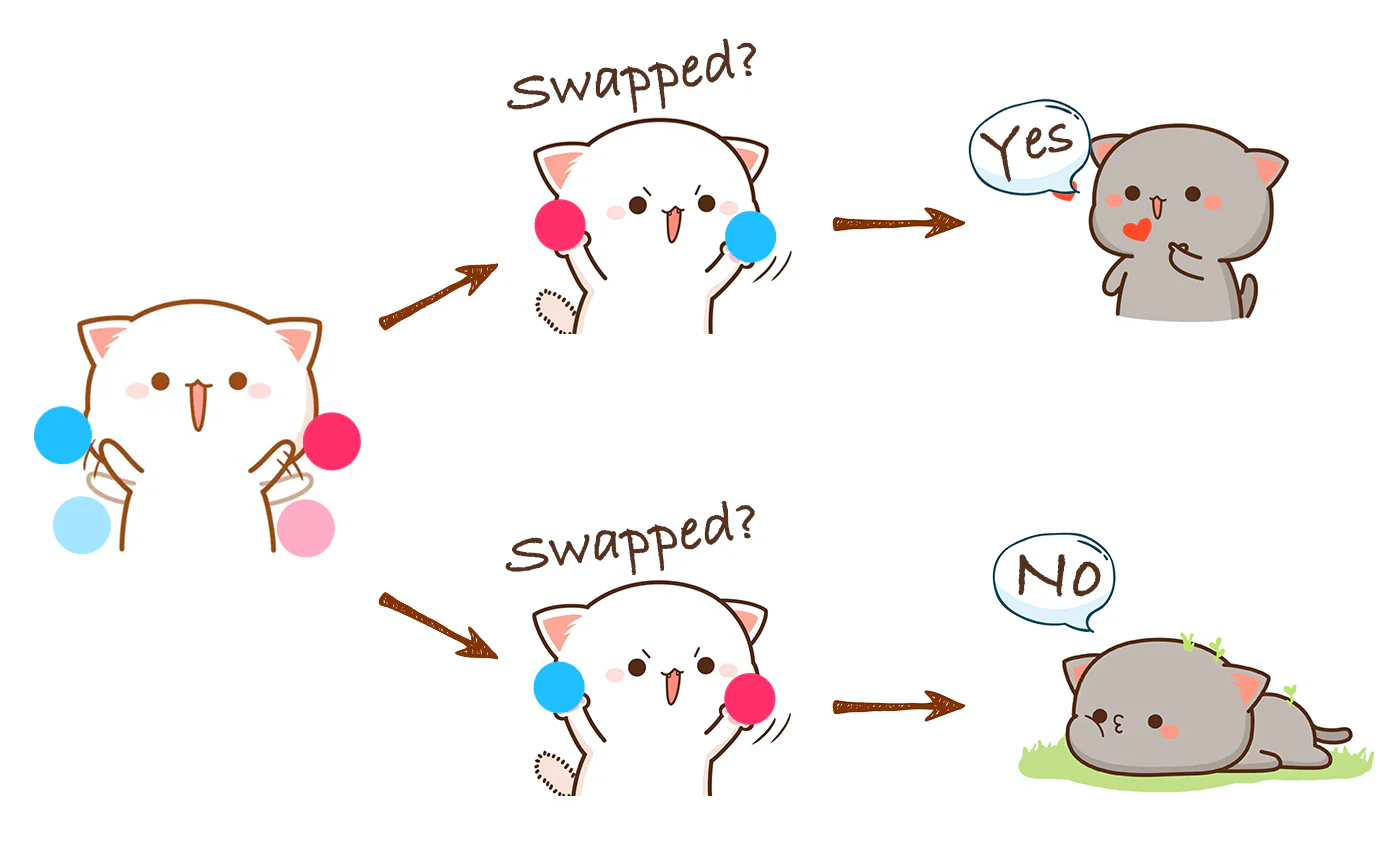
上述证明过程是典型的零知识证明:
- 验证者无法在证明过程中获得任何关于颜色的知识,因为经过验证过程后他依然没有区分颜色的能力。
- 该验证过程是概率性的而非决定性的。
- 该过程是交互式的,需要多轮交互。不过,零知识证明中也有许多协议,通过高级技巧将证明过程转化成了非互动式的。
掌握知识的证明
我们已经分享了一种现实世界中的零知识证明的例子,接下来再来看一下在二进制世界中如何实现零知识证明。
Arthur 是 Elon 的朋友,并且知道对方的手机号。Betty 不知道 Elon 的号码。如果 Arthur 想要向 Betty 证明他知道,但又不想泄露号码,应该怎么实现呢?

一种不成熟的方案是,Elon 发布自己电话号码的哈希,Arthur 通过一个程序输入哈希的原像,程序进行运算并检查结果。这个方法有一些致命的缺陷:
- 根据哈希,Betty 可以通过暴力破解的方式得到原像,能破解出来的概率是不可忽略的,而且得到的结果几乎是确定性的。
- Arthur 必须向该程序输入原像。如果程序在 Arthur 的电脑上,Betty 就会对此有疑问:我怎么知道你有没有作弊,你的电脑也许会一直声称你的证明是对的?
- 如果程序在 Betty 的电脑上运行,Arthur 也会担心,自己输入的信息会不会被窃取,即使程序肉眼可见的代码中并没有窃取信息的命令。
- 因为无法将程序分开在不同的环境中运行,这个信任问题是难以解决的。
常规的方法在这里碰壁了,是时候让零知识证明出场了!
基于密码学的零知识证明的实现方案
在此我会用零知识证明中的 Sigma Protocol 来解决问题,因为它比较简单。并且,为了简洁和易于理解,这里不会使用严格的密码学和数学中的定义、术语及推导过程等。
核心流程
使用零知识证明证明一个人有特定的知识,我们采取如下办法:
- 定义一个
P阶的有限群及其生成元g。我们可以暂时忽略这些奇怪的名词具体什么意思。 - 根据上面的定义,某个拥有知识或能接触到知识的第三方,将知识(记为
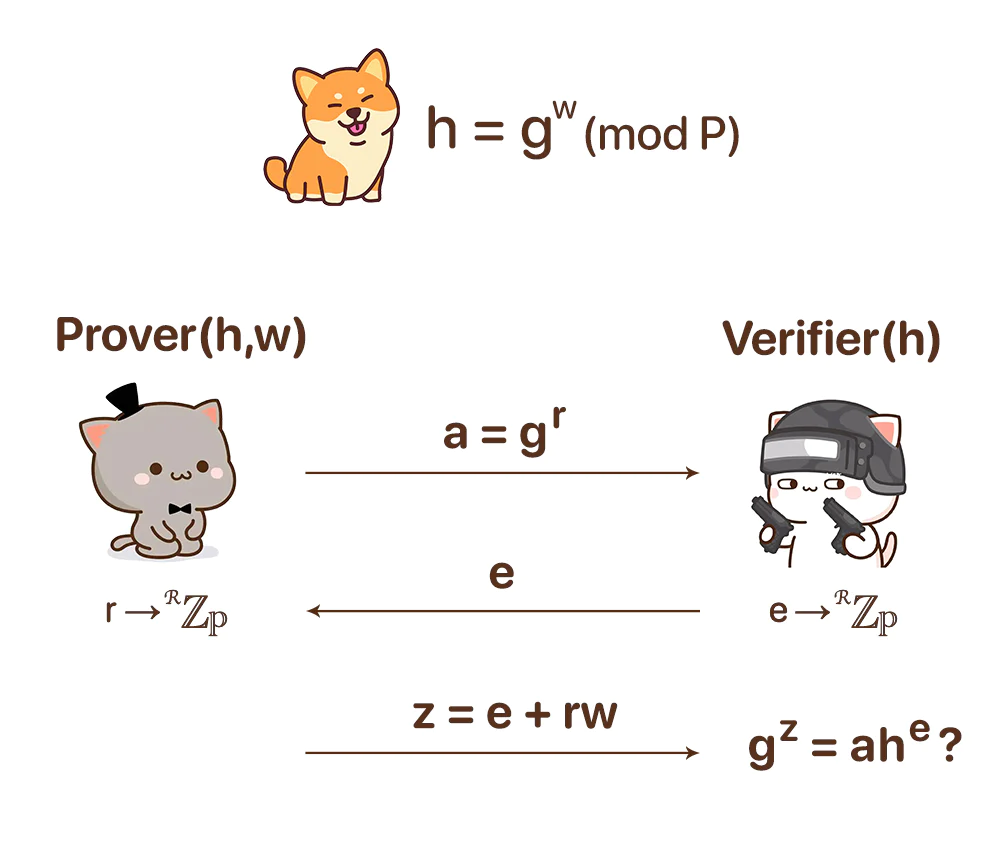
w)通过h = g^w (mod P)的方式加密后,将 h 发布出去。 - 证明者启动零知识证明流程。生成一个随机数 r,计算
a = g^r,并将a发送给验证者。 - 验证者生成一个随机数
e并发送给证明者。 - 证明者计算
z = r + ew并发送给验证者。 - 验证者检查
g^z == a·h^e(mod P)。如果为真,则验证者确实掌握其声称的知识。
好啦,该证明协议到此就结束了!非常简短,但你仍可能对上面的一些数学运算感到困惑,但这不要紧,我们先有个大概印象再深入理解。
示例程序
我用 Python 写了一个简化的 Sigma Protocol 的示范程序,对理解上述过程有很大帮助。在程序中,你既可以扮演定义和发布知识的第三方,也可以成为掌握了知识或没有掌握知识的证明者。
from random import SystemRandom
# Cryptography Public Parameters
g = 22500 # Generator of the finite group
P = 3213876088517980551083924184682325205044405987565585670609523 # Order of the finite group. A big prime number.
# The encrypted knowledge, will be set by a 3rd party.
# Its preimage, which the prover needs to prove he knows, is not accessible to both the prover and verifier.
h = None
# These parameters will be set in further proving steps and passed from the verifier to the prover or vice versa.
a = e = z = None
def specifyKnowledge(w):
global h
h = pow(g,w,P)
print('\n'+'The knowledge topic has been designated.'+ '\n' +
'Neither the verifier nor prover can read since it\'s discarded after this func executed.' + '\n' +
'Only its encryption is publicly known.' '\n' +
'If the prover hasn\'t learned it somewhere else before, he won\'t be able to pass the verification.''\n')
class Verifier:
def __init__(self):
return
def verify_step1(self):
global e
e = SystemRandom().randrange(P)
print('Verifier:')
print('random number b = ',e,', b -----> Prover','\n')
def verify_step2(self):
print('Verifier:'+'\n'+'Checking if pow(g,z,P) == (a * pow(encryptedKnowledge,b,P)) % P:')
if pow(g,z,P) == (a * pow(h,e,P)) % P:
print('Accept! Prover knows the knowledge','\n')
else:
print('Reject! Prover knows nothing','\n')
class Prover:
def __init__(self, knowledge_to_verify):
self.k = knowledge_to_verify
self.r = SystemRandom().randrange(P)
print('Start proving','\n')
def prove_step1(self):
global a
a = pow(g,self.r,P)
print('Prover:')
print('random number r = ',self.r)
print('a = g ** r % p = ',a,', a -----> Verifier','\n')
def prove_step2(self):
global z
z = self.r + e * self.k
print('Prover:')
print('z = r + b * knowledge_to_verify = ',a,', z -----> Verifier','\n')
print('\n'+'-------- Zeroknowledge Example Begins --------'+'\n')
specifyKnowledge(w = int(input("Enter your secret knowledge (Intger):")))
prover = Prover(knowledge_to_verify = int(input("Enter Prover's knowledge (Intger) :")))
verifier = Verifier()
prover.prove_step1()
verifier.verify_step1()
prover.prove_step2()
verifier.verify_step2()Source code:
dysquard/SimpleZkpExplanation · GitHub
Just python example.py.
数学原理
这套流程背后的核心数学原理是离散对数难题:当 P 是一个很大的质数时,对于给定的 h,很难找到满足 h = g^w(mod P)的 w。该原理适用于上面所有类似的式子。
我们来一步一步解析下:
经过加密的知识 h = g^w (mod P),是难以被暴力破解的。由于求余运算的特点,即使被破解了也不具备单一确定解。这意味着对证明者而言,通过暴力破解来作弊,欺骗验证者,是不可行的。
然后我们将 3,4,5 步作为一个整体来看一下他们为什么要交换这些随机数:
I. 证明者并不想暴露其秘密,所以他必须用随机数包裹一下将其隐藏起来。而验证者也需要通过添加一些随机数,让该知识可被自己验证的同时防止证明者作弊,而且不会窥探到证明者的秘密。
II. 如果验证者先发送了随机数 e(即将 3 和 4 步交换一下),很明显,证明者可以通过编造 a = g^z·h^-e 来在最终检查中欺骗验证者,即使没有知识也可以通过。所以证明者必须先手发送一个承诺 (a=g^r),但非 r 本身,来避免可作弊场景,同时不让验证者通过 w = (z - r)/e 提取到秘密。
III. 在收到承诺后,证明者向验证者发送随机数 e。由于其本身或者其衍生物无法泄露任何一方的信息,这个数不需要加密。之后证明者计算 z = r + ew 并将 z 发送给验证者。验证者最终通过检查 g^z= g^(r+ew)= g^r·(gw)^e= a·h^e 来确定证明者是否掌握知识。
通过这种往返交错的结构,我们收获了三个性质:
完备性:
当且仅当证明者输入正确知识,验证才能通过。
可靠性:
当且仅当证明者输入错误知识,验证才会失败。
零知识性:
验证者无法在验证过程中获取任何知识。
上述三点即零知识证明的核心特性。通过数学和密码学,我们构建出了一套光怪陆离的证明体系。恭喜你一路走了这么远,现在应该已经可以说正式迈入了富丽堂皇又奥妙无穷的 ZKP 圣殿。
Have fun!
进一步了解
模拟器和零知识性
我们现在来考虑一些魔幻场景。如果一个证明者具有预言或篡改验证者生成的随机数的超能力,我们称其为模拟器。

设想,模拟器在验证者的随机数 e 生成前就对其进行了篡改,确保其生成后是自己预设的值。根据上面 II 所说,这种能力使模拟器能编造承诺 a 来欺骗验证者。不论模拟器的输入是什么,验证者总会得出结论模拟器具有知识,然而实际上他并没有。
显然,经过这种思想实验我们可以得出结论,验证者无法在该零知识证明协议中获取任何知识,也即其零知识性是成立的:
零知识性 <== ∀模拟器 S,使得 S(x) 与真实的协议执行不可区分,其中 S(x):
选择随机的 z 和 e,令 a = g^z·h^-e,其中 (a,e,z) 的分布与真实的随机数环境一致并满足 g^z=a·h^e。
抽取器和可靠性
再来想象一下另一种超能力者——抽取器,具有时光倒流的能力。不过这次是抽取器作为验证者,面对一个正常的证明者。
当协议结束时,抽取器发起时间倒流,回到协议的起点,并持有上一轮得到的 (z, e, a) 。现在,协议重新执行一遍。由于证明者没有超能力无法进行时间旅行只能在固定的时间线上做确定的事,他又生成了一个一模一样的随机数 r 以及承诺 a = g^r,而抽取器则可以生成新的随机数 e'给证明者。
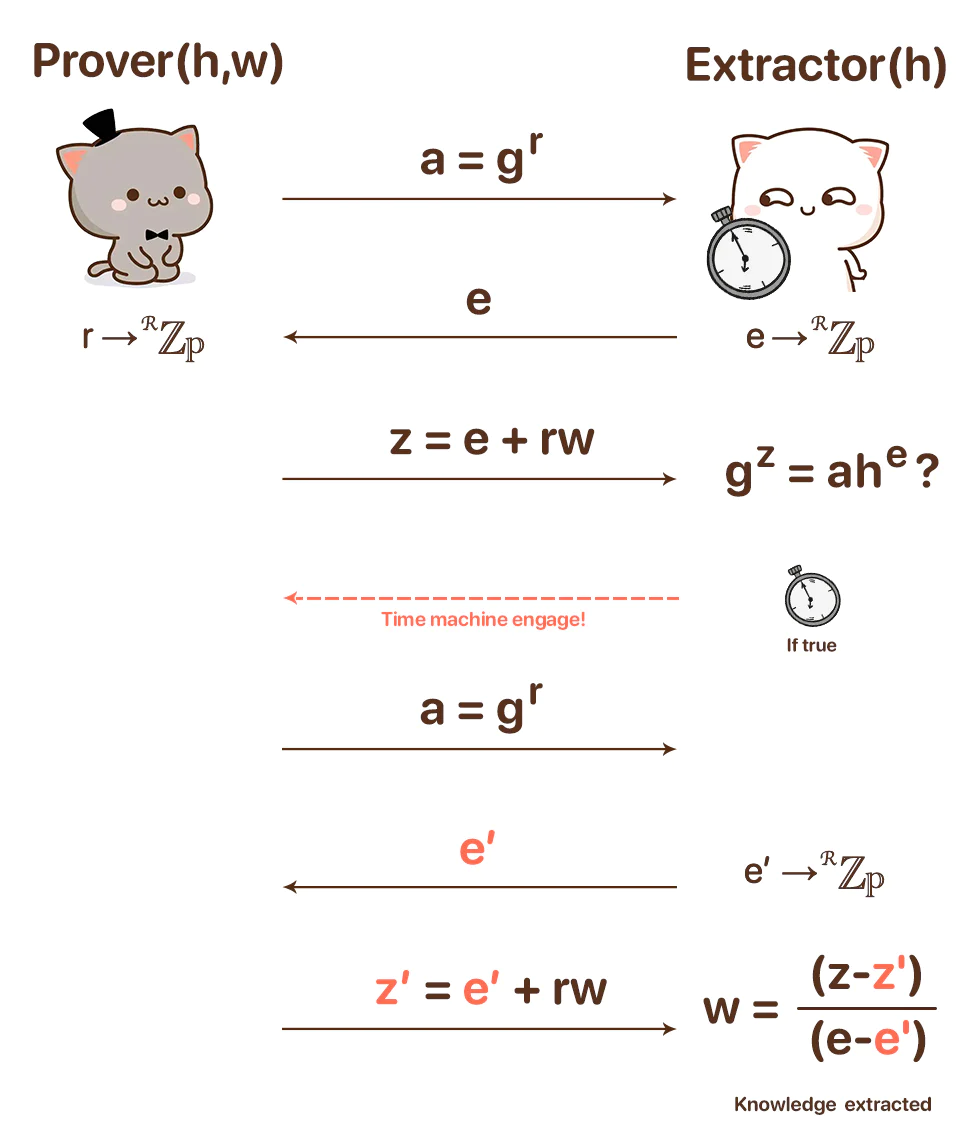
现在,抽取器获得了:g^z= a·h^e, g^z'=a·h^e => g^(z-z') = h(e-e') => 加密后的知识 h = g^((z-z')/(e-e')) => 知识 w = (z-z')/(e-e').
显然,只要证明者真的掌握了知识,抽取器总是可以将其抽取出来,也即完备性成立:
完备性 <== ∀抽取器 E,对给定的任何 h,在掌握 (a,e,z),(a,e',z')且 e≠e'的情况下,都能输出 w s.t. (h,w) ∈ R.
完备性
完备性不需要任何特殊角色来证明,因为:g^z = g^r+ew = g^r·(g^w)^e = a·h^e.
免责声明:作为区块链信息平台,本站所发布文章仅代表作者及嘉宾个人观点,与 Web3Caff 立场无关。本文内容仅用于信息分享,均不构成任何投资建议及要约,并请您遵守所在国家或地区的相关法律法规。



















