ECDSA 门限签名典型算法介绍

没有最好的，只有最合适的

作者：Cobo 密码学团队，Cobo Global

原用标题：Cobo 密码知识讲堂｜第三讲：ECDSA 门限签名典型算法介绍

封面：Photo by Batyrkhan Shalgimbekov on Unsplash

随着香港开始允许散户交易数字资产，数字资产也在逐步走进每个人的生活，数字资产、数字签名等新概念层出不穷。Cobo 密码知识讲堂计划推出以 “门限签名” 为主题的系列科普文章，旨在以深入浅出的方式，带领读者了解数字签名中门限签名的技术本质和应用原理。该系列科普文章每一篇内容相互独立又互相补充，涵盖门限签名的概念及典型应用、ECDSA 门限签名的设计及发展现状、Schnorr 门限签名的设计及发展现状、基于门限签名的账户体系构建，以及层级化门限签名设计等多个该领域的热点和难点问题，力求通过对技术研究的深层次剖析和解读，让读者对门限签名领域有更加深刻的理解。

《Cobo 密码知识讲堂｜第一讲：门限签名的概念与应用》

《Cobo 密码知识讲堂｜第二讲：ECDSA 算法及其门限化设计介绍》

本讲概述：本期课程介绍 ECDSA 门限签名，首先对当前已有的 ECDSA 门限签名算法的技术路线进行归纳和总结，绘制其技术发展的 “科技树”；随后，针对 ECDSA 门限签名算法实现的不同技术途径，进行针对性的介绍，阐述其设计原理、核心组件和技术迭代过程；最后，结合学术研究基础和产业界业务经验，给出 ECDSA 门限签名算法使用的相关建议，以供参考

Part 1：ECDSA 门限签名 “科技树”

随着比特币等加密数字货币的迅速发展，ECDSA 门限签名算法已经得到学术界和产业界的重点关注，充分的科研资源投入使得近些年来涌现出大量研究成果。这些科研成果的设计目标是一致的，即具备高安全性、低计算与通信复杂度和计算过程可审计的 ECDSA 门限签名算法。然而它们的设计重点、技术途径、使用的密码学技术各不相同，既存在一定程度的 “技术继承”，也具备 “技术独立” 的特征。在充分研究的基础上，我们对 ECDSA 门限签名算法的 “科技树” 进行梳理，澄清不同研究成果之间的技术关联关系和继承关系，具体见图 1。

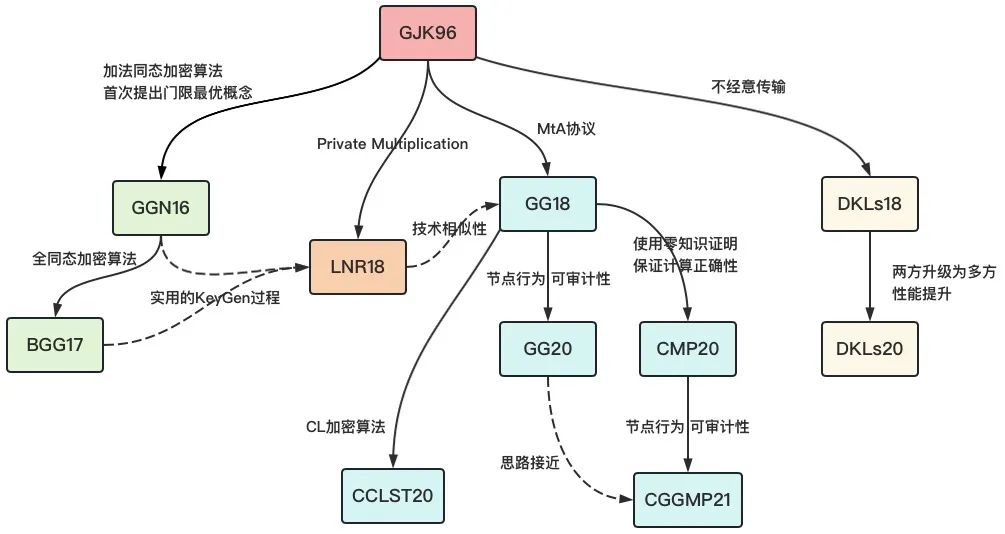
整体而言，GJK96 是第一个 ECDSA 门限签名方案，其设计思路也非常直观朴素，而且并未满足门限最优的性质。以 GJK96 为基础，围绕门限最优、高效性、可审计性等设计目标，出现了一系列的技术方案。以实现门限最优的技术途径为基本分类维度，这些方案大致可以分为四个技术体系：基于分布式同态加密、基于 MtA 协议、基于 Private Multiplication 协议和基于不经意传输。在下一部分，我们对这四个技术体系的代表性方案进行详细介绍。

Part 2：典型 ECDSA 门限签名算法介绍 GJK96：ECDSA 门限签名方案的先驱

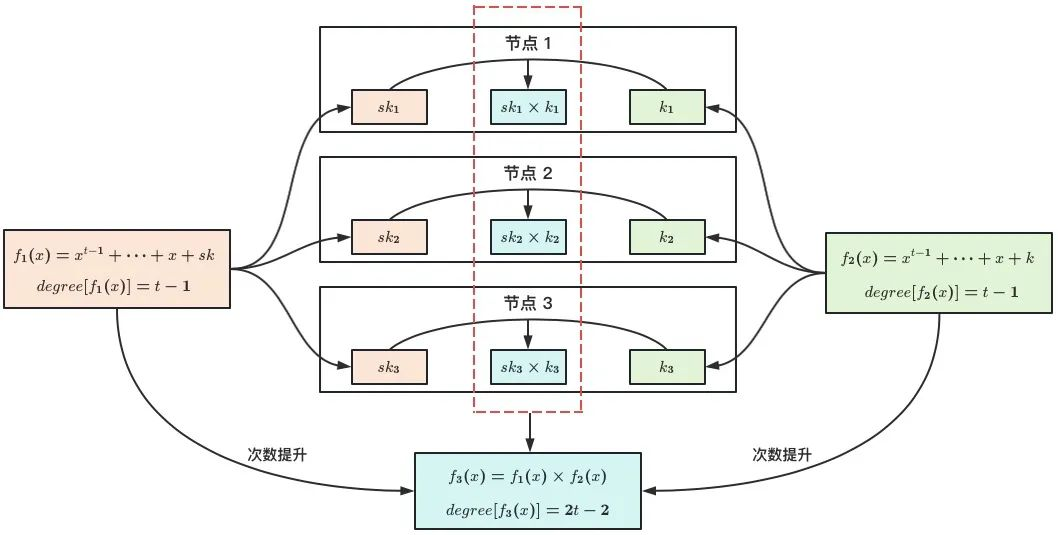
在 GJK96   中，私钥   和签名随机数   是以秘密碎片的形式存在于   个节点，每个节点   保存碎片   和  。而签名过程中   的碎片是直接将   和   相乘得到，导致秘密分享多项式的次数由   提升为  （见图 2），从而不具备门限最优的性质，即恢复私钥仅需   个节点参与，但是完成门限签名则需   个节点。GJK96 作为首个 ECDSA 门限签名方案，扮演了 “吃螃蟹” 的角色，具有先驱意义。然而由于其非门限最优的缺陷，使得在实际账户管理中需要部署比安全门限（即  ）更多的服务器，在提高了运营成本的同时，也增加了账户安全风险，并不适用于当前场景需求。

GGN16 / BGG17：基于分布式同态加密的 ECDSA 门限签名方案

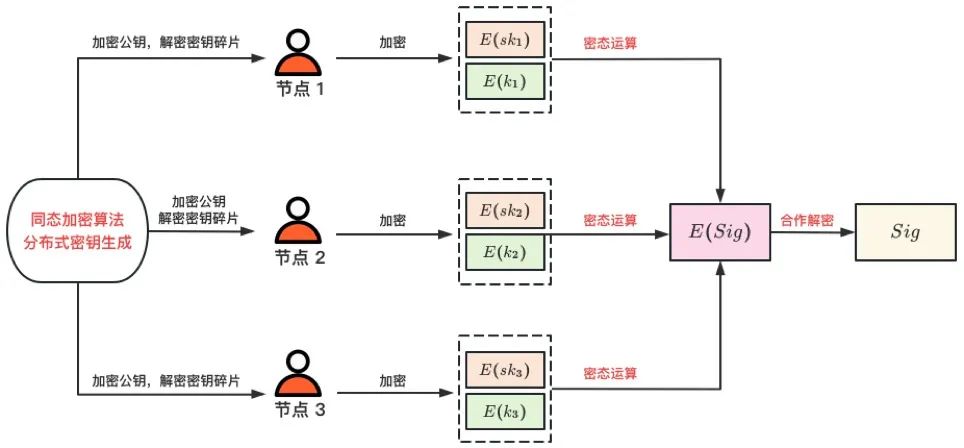
GGN16   首次提出了 “门限最优（Threshold Optimality）” 的概念，并设计了首个 ECDSA 门限最优签名算法。其设计思路（见图 3）在于将计算签名所需要的参数通过加法同态加密算法进行加密，签名过程是在密态下进行并最终生成签名的密文，最后所有节点合作解密得到签名的明文数据。而其中的关键步骤，在于所有节点通过可信第三方或者公共可验证算法生成一套加法同态加密算法参数，加密公钥公共可知，解密私钥则以碎片的形式分布在各节点。BGG17   与 GGN16 的设计思路类似，其改进在于将加密算法由加法同态加密算法替换为一阶同态加密算法，使得对加密后的参数进行任意次加法以及深度为 1 的乘法运算均能保证同态性，从而降低节点交互的次数，由 6 轮降低为 4 轮。

基于分布式同态加密的 ECDSA 门限签名方案虽然实现了门限最优的性质，但是也存在非常致命的问题，即可实现性/实用性未知，因为节点个数超过 2 时，如何分布式生成一个同态加密算法（如 Paillier Encryption）的密钥，是一个不确定的问题。

GG18 / GG20 / CCLST20 / CMP20 / CGGMP21：基于 MtA 协议的 ECDSA 门限签名方案

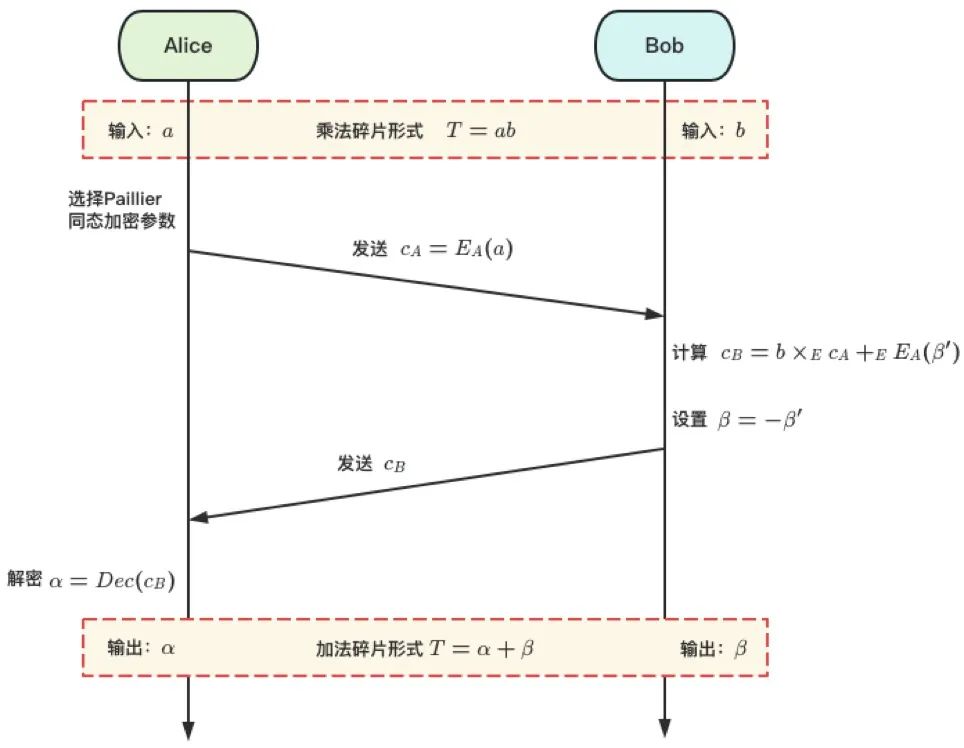
基于 MtA 协议的 ECDSA 门限签名是当前非常主流的一种实现方式，已经大范围地被应用到实际的业务场景中。该方案的核心在于基于 MtA 协议（Multiplication to Addition）实现了   的计算过程，同时没有引起秘密分享多项式次数的升高，满足了门限最优的性质。MtA 协议基于 Paillier 同态加密算法实现，协议输入是乘法秘密碎片   和  ，满足  ，协议输出是加法秘密碎片 α  和 β ，满足 αβ ，具体运行流程见图 4。

GG18   是首个基于 MtA 协议实现的 ECDSA 门限签名方案。GG20   是对 GG18 的改进，一方面实现了可验证终止性（Identifiable Abort），另一方面将签名的过程拆分为预处理阶段（Preprocess Stage）和在线阶段（Online Stage），线上仅需一轮交互即可完成签名。CCLST20   是将 GG18 中使用的 Paillier 同态加密算法替换位 CL 同态加密算法，从而避免了由 Paillier 模数和 ECDSA 模数不一致导致的、需要引入大量零知识证明完成范围证明的计算负荷。CMP20   则是将关注点放在计算过程的安全性保障上，通过在各个步骤引入对应的零知识证明，从而保证签名过程的安全性，避免了由于签名失败而导致的敏感信息泄漏风险，是对 GG18 中签名结果正确性验证方法（即步骤 5A-5E）的有效提升。CGGMP21   是对 CMP20 的提升类似于 GG20 对 GG18 的提升，即增加了节点行为的审计性，给出两个不同的解决方案，即一个方案是 4 轮交互和   的计算复杂度，另一个方案是 7 轮交互和   的计算复杂度。

LNR18：基于 Private Multiplication 协议实现的 ECDSA 门限签名方案

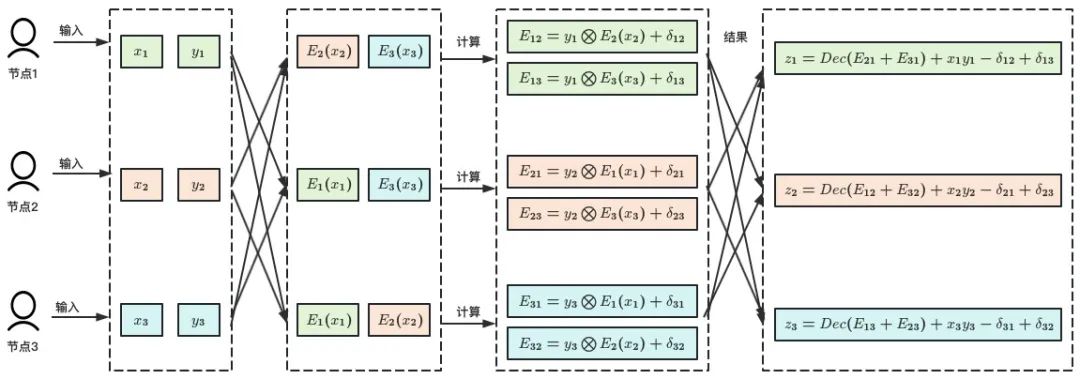
LNR18   和 GG18 有很深的渊源，二者都是在 CCS18 上同期发表的论文，因此技术途径具备非常强的相似性，但是侧重点又不同。LNR18 的设计出发点在于对 GGN16 和 BGG17 的 KeyGen 阶段实用性的质疑，即分布式生成一个同态加密算法密钥是困难的。基于这一认识，LNR18 设计了一个 “双层” 协议，上层是将 Paillier 同态加密算法替换为 ElGamal 算法，由于 ElGamal 算法非常强的线性特征，因此其分布式密钥生成实现简单。但是需要强调的是，协议中对 ElGamal 算法的使用是在指数上执行（ElGamal in-the-exponent），因此并不会直接解密得到明文，而是得到明文的椭圆曲线倍点，从而完成计算过程正确性的验证，类似于 GG18 的 5A-5E 过程。下层则是协议的核心，基于 Private Multiplication 协议完成签名的实际计算过程。Private Multiplication 协议的工作流程见图 5，其基本设计思路与 MtA 协议类似，都依赖于同态加密算法实现，但是对扰动项的处理方式不同，Private Multiplication 协议是在形成最终输出前统一消除，而 MtA 协议则是在两两交互过程中消除。

DKLs18 / DKLs20：基于不经意传输实现的 ECDSA 门限签名方案

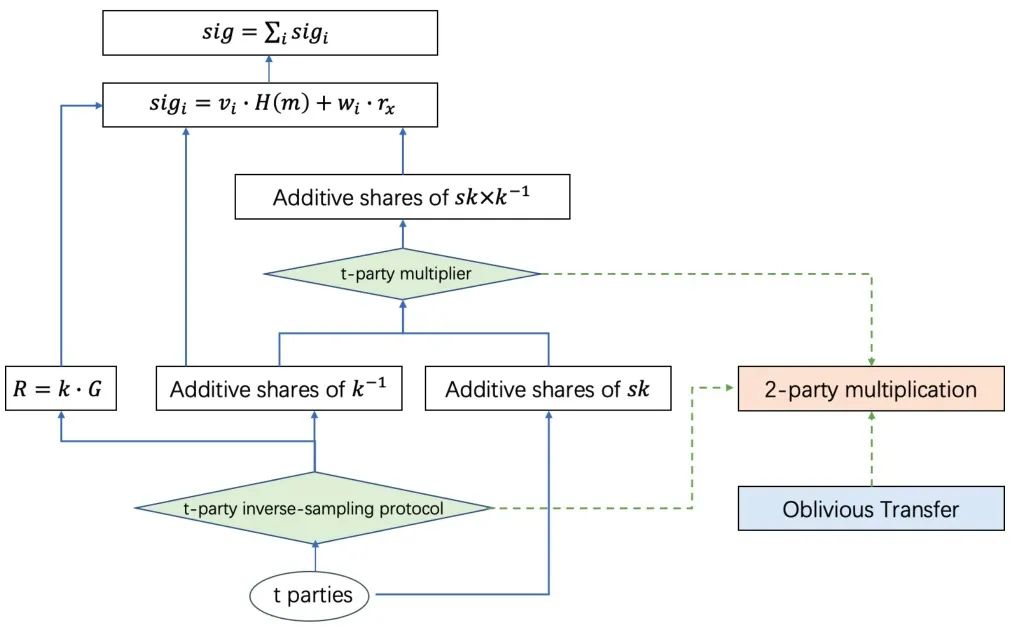
DKLs18   和 DKLs20   是基于相关不经意传输（Correlated Oblivious Transfer，简称 COT）实现的 ECDSA 门限签名方案，与之前的技术途径存在比较明显的差异，当然这不代表其底层的密码学技术不同，因为 COT 的实现也是依赖同态加密。DKLs18 是针对两方的 ECDSA 门限签名方案，而 DKLs20 在其基础上了改进，扩展为多方的 ECDSA 门限签名方案，同时对通信和计算过程进行了优化，实现 40% 性能提升。DKLs20 的协议流程见图 6，核心组件为 2-Party Multiplication，其功能类似于 MtA 协议，是基于 COT 实现。基于 2-Party Multiplication，实现了 t-party Inverse-sampling 协议和 2-party Multiplier 协议，分别完成求逆运算和乘法运算，最终实现完整的签名过程。

Part 3：ECDSA 门限签名算法使用攻略

本文内容共涉及到 11 种 ECDSA 门限签名算法，还有很多其他算法没有体现，此外随着学术界的持续研究，可以预见未来会有更多的门限签名算法出现。那么究竟该选择哪个 ECDSA 门限签名算法作为数字资产多方管理的解决方案？是一个值得思考的问题。基于学术研究基础和产业界业务经验，本文给出如下建议供参考。

没有最好的，只有最合适的

不同的 ECDSA 门限签名算法在设计之初，就有不同的侧重点，或是侧重效率的提升（如优化通信轮数），或是侧重安全证明（如降低安全假设），或是侧重节点行为可审计性（如增加额外可验证数据）。无论是哪个侧重点，都是在不同性质之间做 Tradeoff。因此，选择 ECDSA 门限签名算法的核心，还是要把握自身需求，选择最适配的算法，而非唯新论、唯复杂论。Cobo 对 ECDSA 门限签名算法的选择，是以整个领域的研究成果为基础，结合实际业务和客户的需求，综合考虑安全和性能，最终选择最合适的方案。

保持对技术的敬畏之心

ECDSA 签名算法本身是 Threshold Unfriendly 的，因此其门限化的设计比其他签名算法（如 Schnorr、BLS）要复杂很多。具体体现在两个方面：一个是使用到的密码学技术复杂，如同态加密、零知识证明、不经意传输等；另一个是攻击模型复杂，复杂的算法带来的是复杂的攻击手段，因此需要谨慎设计，避免安全漏洞。目前大部分的算法都提供了形式化证明，可以理解为可证明安全的，如此精细的算法，不存在任何冗余的操作和组件。之前就出现过类似的案例  ，即工程实现的时候遗漏了论文中关于 Paillier 加密算法的公共参数 N 的零知识证明，最终导致在签名交互过程中诚实节点私钥碎片泄漏的风险。因此在实际使用 ECDSA 门限签名算法时候，要保持对技术的敬畏之心，严格按照协议标准实现，避免出现安全风险。

参考文献

1. Gennaro R, Jarecki S, Krawczyk H, et al. Robust threshold DSS signatures[C]//International Conference on the Theory and Applications of Cryptographic Techniques. Springer, Berlin, Heidelberg, 1996: 354-371.
2. Gennaro R, Goldfeder S, Narayanan A. Threshold-optimal DSA/ECDSA signatures and an application to Bitcoin wallet security[C]//International Conference on Applied Cryptography and Network Security. Springer, Cham, 2016: 156-174.
3. Boneh D, Gennaro R, Goldfeder S. Using level-1 homomorphic encryption to improve threshold DSA signatures for bitcoin wallet security[C]//International Conference on Cryptology and Information Security in Latin America. Springer, Cham, 2017: 352-377.
4. Gennaro R, Goldfeder S. Fast multiparty threshold ECDSA with fast trustless setup[C]//Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security. ACM, New York, NY, 2018: 1179-1194.
5. Gennaro R, Goldfeder S. One Round Threshold ECDSA with Identifiable Abort[J].  IACR Cryptol. ePrint Arch., 2020, 2020: 540.
6. Castagnos, G., Catalano, D., Laguillaumie, F., Savasta, F., Tucker, I. Bandwidth-Efficient Threshold EC-DSA[C]//Public-Key Cryptography – PKC 2020. Lecture Notes in Computer Science(), vol 12111. 
7. R. Canetti, N. Makriyannis, and U. Peled. Uc non-interactive, proactive, threshold ecdsa[J]. IACR Cryptol. ePrint Arch., 2020, 2020: 492.
8. Canetti R , Gennaro R , Goldfeder S , et al.UC Non-Interactive, Proactive, Threshold ECDSA with Identifiable Aborts[C]//2020 ACM SIGSAC Conference on Computer and Communications Security.
9. Y. Lindell and A. Nof. Fast secure multiparty ECDSA with practical dis- tributed key generation and applications to cryptocurrency custody[C]//ACM CCS 2018, pages 1837–1854.
10. J. Doerner, Y. Kondi, E. Lee, and a. shelat. Secure two-party threshold ECDSA from ECDSA assumptions[C]//In 2018 IEEE Symposium on Security and Privacy, pages 980–997. 
11. J. Doerner, Y. Kondi, E. Lee, and a. shelat. Threshold ECDSA from ECDSA assumptions: The multiparty case[C]//In 2019 IEEE Symposium on Security and Privacy, pages 1051–1066.
12. BitGo Wallet Zero Proof Vulnerability: Technical Report.[EB/OL]. (2023-03-17) [2023-06-10].https://www.fireblocks.com/blog/bitgo-wallet-zero-proof-vulnerability/

免责声明：作为区块链信息平台，本站所发布文章仅代表作者及嘉宾个人观点，与 Web3Caff 立场无关。文章内的信息仅供参考，均不构成任何投资建议及要约，并请您遵守所在国家或地区的相关法律法规。