Beosin 安全研究：ERC-7520 草案詳解 zk-SNARK 公共輸入溢出攻擊防護

ZKP 專案方看過來

作者：Saya，Bryce，Beosin 安全研究專家

1. 什麼是零知識證明

零知識證明（Zero-Knowledge Proof，後文簡寫 ZKP）是一種密碼學概念，它可以用來證明某個聲明的真實性，而無需透露有關該聲明的任何具體資訊。 在零知識證明中，證明者可以向驗證者證明某個陳述是正確的，而驗證者只會得到一個結果：要麼接受該陳述的真實性，要麼拒絕它，而無需瞭解證明的具體細節。

這個概念可以用一個簡單的例子來解釋。 假設有兩個人，一個是證明者和一個是驗證者。 證明者想向驗證者證明自己知道一個秘密的密碼，而不泄露密碼本身。 在傳統的方式中，證明者可能會告訴驗證者密碼是什麼，但在零知識證明中，證明者可以使用特殊的協定來向驗證者證明他知道密碼的正確性，而不泄露密碼本身。

目前常見的零知識證明系統演算法包括 zk-SNARKs、zk-STARKs、BulletProofs 等。

2. ZKP 在區塊鏈中的應用

在區塊鏈技術中，ZKP 有多種應用，例如提升隱私、改善可擴展性和安全性等。 以下是 ZKP 在區塊鏈中的一些關鍵應用：

1 隱私保護：

區塊鏈是公共的，這意味著任何人都可以查看鏈上的所有交易。 然而，有時候，使用者可能希望保持他們的交易資訊保密。 ZKP 允許使用者證明他們擁有足夠的資金進行交易，同時不必公開他們的資金總額。 這大大增強了用戶的隱私保護。 例如，Zcash 是一種使用零知識證明技術的加密貨幣，它允許使用者隱藏交易的發送者、接收者和金額。

2 計算壓縮與區塊鏈擴容：

區塊鏈的可擴充性是一個挑戰，尤其是在大規模應用中。 ZKP 可以用於減輕節點的負擔，提高整個系統的可擴充性。 通過使用 ZKP 驗證交易的有效性，節點無需查看完整的交易歷史記錄，從而減少了存儲和處理的負擔，目前應用最廣泛的 ZK Rollup 是一種擴展性解決方案，旨在提高乙太坊及其他區塊鏈網路的輸送量和效率。 它結合了 Rollup 和 ZKP 技術的優勢，提供了高性能的去中心化應用程式（DApps）擴展方案。 在傳統的乙太坊網路上，每個交易都需要被驗證和記錄在區塊鏈上，這導致了交易處理的延遲和高成本。 而 ZK Rollup 通過將大量的交易批量處理並壓縮為單個區塊，ZKP 則用於證明批量交易的有效性，從而確保交易的正確性和安全性。

3 身份驗證：

零知識證明可以用於驗證使用者的身份而無需透露敏感的個人資訊。 例如，一個人可以使用零知識證明向網路證明他們滿足某個特定的年齡要求或擁有某種特定的證書，而無需揭示他們的確切年齡或其他身份資訊。

4 去中心化存儲：

伺服器可以向使用者證明他們的數據被妥善保存，並且不洩露數據的任何內容。

總的來說，區塊鏈的零知識證明在隱私保護、計算壓縮與擴容、身份驗證、去中心化存儲等方面有著廣泛的應用。 它為區塊鏈技術提供了更多的功能和選擇，推動了區塊鏈在不同領域的發展和應用。

3. ZKP 應用中的雙花攻擊

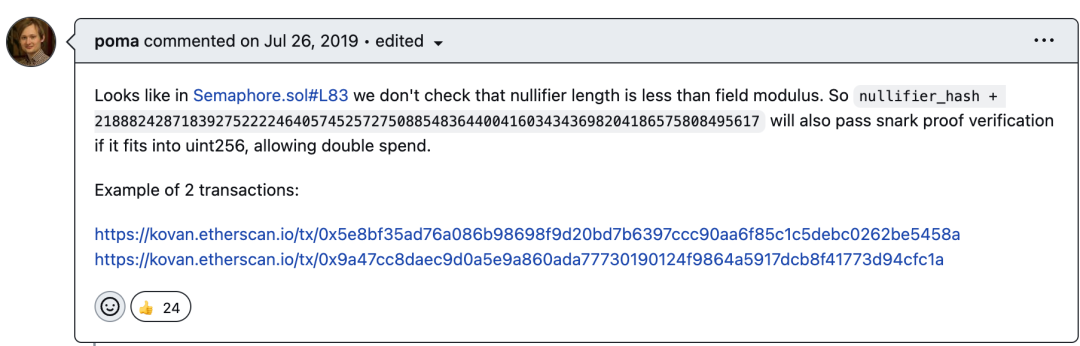
zk-SNARK（Zero-Knowledge Succinct Non-Interactive Argument of Knowledge）是一種基於零知識證明的技術，可以在不洩露真實資訊的情況下證明某個聲明的真實性。 它是一種非常高效的零知識證明技術，可以在非常短的時間內生成和驗證證明，同時保護隱私和安全性，所以應用非常廣泛。 但是，伴隨著應用的擴展，其安全性也越來越受到關注。 我們在不久前就曾發現了其通用漏洞：ZKP 專案中如果未正確校驗 verify 函數中參數 input 的取值範圍，攻擊者可以偽造多個 input 通過校驗，造成雙花攻擊。 這種攻擊影響範圍非常廣，涉及多個 zk-SNARK 演算法包括：groth16、plonk 等，並且 solidity、js 等多種開發語言均存在該漏洞。 該漏洞最開始由 poma 在零知識證明專案 Semaphore 上首次發現，並給出了兩筆成功實施的交易範例，具體如下圖所示：

該漏洞具體的攻擊原理是，如果要在乙太坊中生成和驗證 zk-SNARK 證明，需要使用 F_p-arithmetic 有限域橢圓曲線電路，其中 p 值用於確定橢圓曲線有限域的範圍，所以電路的 input 取值範圍為 [0,1,...,p-1]。 不同的曲線擁有不同的 p 值：

EIP-196 中定義的 BN254 曲線（也稱為 ALT_BN128 曲線）：

p = 21888242871839275222246405745257275088548364400416034343698204186575808495617

circom2 引入了兩個新的素數，即 BLS12-381 曲線：

p = 52435875175126190479447740508185965837690552500527637822603658699938581184513

以及 plonk2：

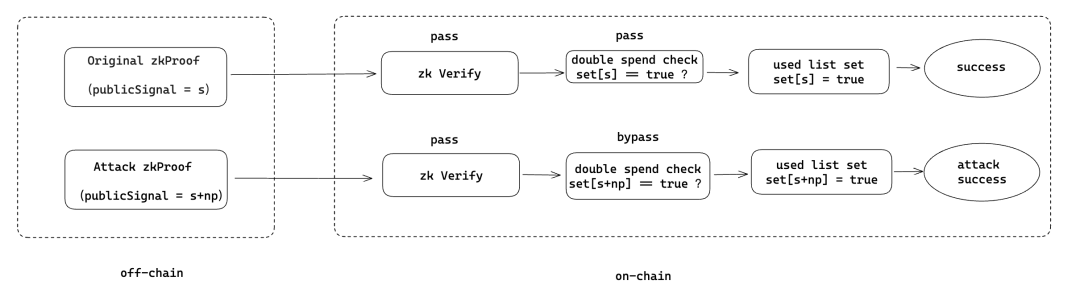
18446744069414584321

但是驗證代碼實現時，不同的程式設計語言中整數變數類型可能遠遠大於電路中 input 的取值範圍，如：solidity 中 uint256 能表示的數值範圍為 ，java 中 lont int 為 [-2^63,2^63-1]，javascript 的 bigint 等，此時存在下列多個 input 經過驗證代碼中的模 p 運算后，可以通過校驗： 綜上， 只要知道了其中一個合法的證明參數 x，變數取值範圍內的 都可通過校驗。 於是攻擊者如果獲取到任意已經驗證通過的 x，即可構造 個 可以通過校驗，具體的攻擊流程如下：

隨後 Semaphore 方確認並修復了該漏洞，ZoKrates、snarkjs 等 zk 庫也同步進行了緊急修復，但 Beosin 安全研究員發現該問題目前並未存在一個統一的解決方案，例如 Semephore 協定將約束寫到 pairing 庫中並未在外層業務邏輯中顯式校驗數據的有效範圍; 而 circom 生成的合約代碼以及 Tornado.Cash 則在 verify 函數中顯式地校驗 SNARK_SCALAR_FIELD，這種混亂不統一的解決方式可能會對很多新的 zk DApp 專案方造成困擾並出現安全隱患，因此我們希望能夠使用一種標準化的方式來解決這個問題。

4. ERC-1922 中的雙花攻擊

目前乙太坊具有一個 zk 相關的標準 EIP-1922，該標準介紹了用於驗證 zk-SNARK 的 Verify 合約標準介面，具體代碼如下：

pragma solidity ^0.5.6;
/// @title EIP-XXXX zk-SNARK Verifier Standard/// @dev See https://github.com/EYBlockchain/zksnark-verifier-standard///  Note: the ERC-165 identifier for this interface is 0xXXXXXXXX.///  TODO: Calculate interface identifierinterface ERC1922 /* is ERC165 */ {    /// @notice Checks the arguments of Proof, through elliptic curve    ///  pairing functions.    /// @dev    ///  MUST return `true` if Proof passes all checks (i.e. the Proof is    ///  valid).    ///  MUST return `false` if the Proof does not pass all checks (i.e. if the    ///  Proof is invalid).    /// @param proof A zk-SNARK.    /// @param inputs Public inputs which accompany Proof.    /// @param verificationKeyId A unique identifier (known to this verifier    ///  contract) for the Verification Key to which Proof corresponds.    /// @return result The result of the verification calculation. True    ///  if Proof is valid; false otherwise.    function verify(uint256[] calldata proof, uint256[] calldata inputs, bytes32 verificationKeyId) external returns (bool result);}

其中，零知識證明 proof、inputs 變數類型都為 uint256[]，該變數類型是目前 ZKP 演算法中橢圓曲線運算最常用的，但是該介面中也未增加對應的安全防護，因此同樣存在雙花攻擊的巨大安全隱患。

5. ERC-7520 解決方案

Beosin 根據上述問題，提出了 EIP-7520 防範這種安全風險，具體為乙太坊生態中所有使用了 zk 技術的 DApp 專案方在 compliant verifier contract 中，都必須實現該介面從而使用規範統一而又安全的方式對所有 input 進行有效範圍校驗，具體介面如下：

pragma solidity ^0.5.6;
/// @title EIP-XXXX zk-SNARK public inputs Verifier Standard///  Note: the ERC-165 identifier for this interface is 0xXXXXXXXX.///  TODO: Calculate interface identifierinterface EIP7520 /* is ERC165 & ERC1922 */ {    /// @notice Checks the arguments of Inputs are within the scalar field    /// @dev    ///  MUST return `true` if Inputs passes range check (i.e. the Inputs are    ///  valid).    ///  MUST return `false` if the Inputs does not pass range check (i.e. if the    ///  Inputs are invalid).    /// @param inputs Public inputs which accompany Proof.    /// @param p Public input which accompany the curve.    function verifyPublicInput(uint256[] inputs，uint256 p) external returns (bool result)；}

verifyPublicInput 函數是這個標準的核心，涉及到的參數具體含義如下：

• inputs ：定義為 uint256[] 類型，代表了 ZKP 專案中 verify 函數涉及到的公共信號參數
• p ：定義為 uint256 類型，該值對應演算法中使用的橢圓曲線的 p 值

下面將對比實現與未實現 EIP-7520 介面的兩種情況下，針對該該攻擊的不同表現，以向各位專案方表明風險：

1 假設我們在不調用本 eip 介面 verifyPublicInput 的情況下，直接使用 verify 合約代碼進行證明驗證，具體代碼如下：

function verify(uint[] memory input, Proof memory proof) internal view returns (uint) {        VerifyingKey memory vk = verifyingKey();        require(input.length + 1 == vk.IC.length,"verifier-bad-input");        // Compute the linear combination vk_x        Pairing.G1Point memory vk_x = Pairing.G1Point(0, 0);        for (uint i = 0; i < input.length; i++)            vk_x = Pairing.addition(vk_x, Pairing.scalar_mul(vk.IC[i + 1], input[i]));        vk_x = Pairing.addition(vk_x, vk.IC[0]);        if (!Pairing.pairingProd4(            Pairing.negate(proof.A), proof.B,            vk.alfa1, vk.beta2,            vk_x, vk.gamma2,            proof.C, vk.delta2        )) return 1;        return 0;}

原始的证明验证通过的实验结果截图：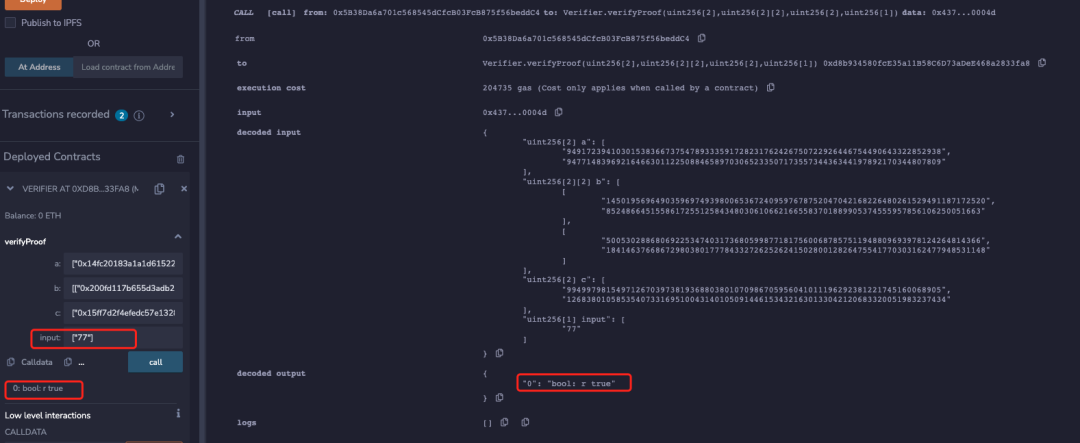

同時，可以偽造如下 4 個證明同樣可以通過驗證，造成雙花攻擊：

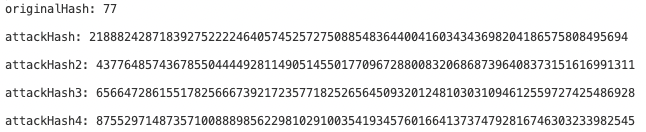
使用其中一個偽造的證明，驗證結果如下圖所示：

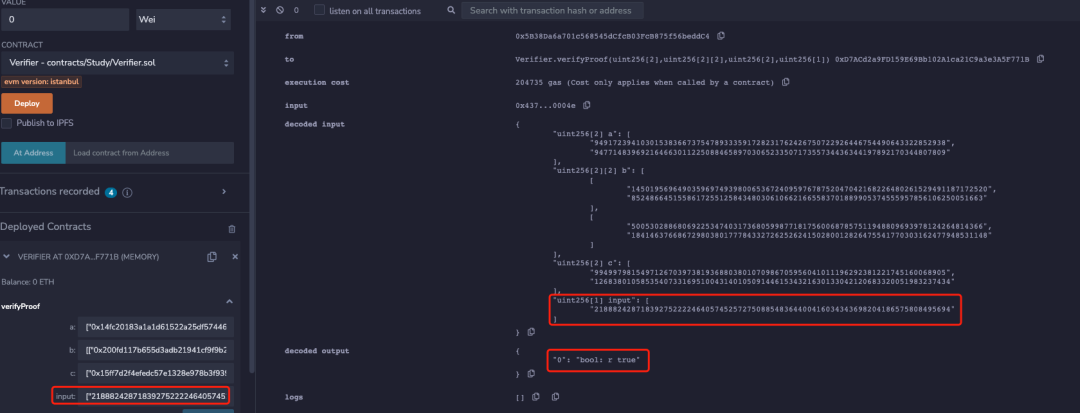
2 如果調用了本 eip 中的 verifyPublicInput 介面，上述偽造的證明則會驗證失敗，部分合約代碼如下，其餘詳細部分可以參考 Reference Implementation：

function verifyx(uint[] memory inputs, Proof memory proof, bytes32 verificationKeyId,uint256 p) public returns (uint){        require(verifyPublicInput(inputs,p),"verifier-over-snark-scalar-field");        require(verify(inputs,proof,verificationKeyId),"verify fail");              return true;}
function verifyPublicInput(uint256[] inputs，uint256 p) internal view returns (bool) {        for (uint i = 0; i < input.length; i++) {            require(input < p,"verifier-gte-snark-scalar-field");                 }        return true;}

实验结果如下图所示：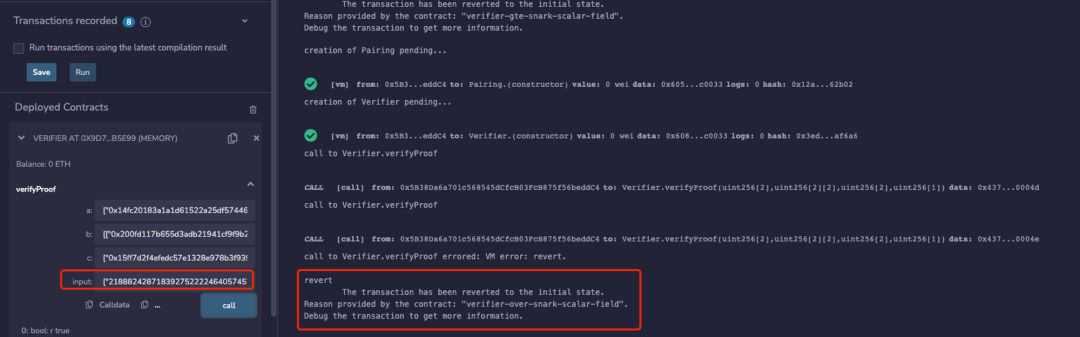

綜上，可以發現如果不使用本介面對公共信號值進行取值範圍的有效性校驗，那麼可能存在雙花攻擊風險。

免責聲明：作為區塊鏈資訊平臺，本站所發佈文章僅代表作者及嘉賓個人觀點，與 Web3Caff 立場無關。 文章內的資訊僅供參考，均不構成任何投資建議及要約，並請您遵守所在國家或地區的相關法律法規。